第1章 牛顿
04-13Ctrl+D 收藏本站

艾萨克·牛顿(1642—1727)
艾萨克·牛顿不但是数学上的开创性人物,而且是整个西方思想史上举足轻重的人物。当他出生时,科学尚未确立对中世纪迷信至高无上的统治地位,而在他去世时,理性时代已经步入全盛时期。这一不同寻常的转变在一定程度上应归功于他的贡献。
作为数学家,牛顿被推崇为微积分或者他为之命名的“流数术”的创立者。微积分的起源要追溯到17世纪60年代中期,那时牛顿还是剑桥大学三一学院的一名学生。在那里牛顿专心研究勒内·笛卡儿(1596—1650)、约翰·沃利斯(1616—1703)以及三一学院第一位卢卡斯数学教授艾萨克·巴罗(1630—1677)这样一些先驱们的著作,但是很快他就发现自己进入了一个从未有人涉足的领域。在接下来的几年中,牛顿永远地改变了数学的面貌,传记作家Richard Westfall把他这几年描绘为一个“光芒四射的活动”时期。1 到1669年,巴罗本人将他的这位继任者和同事形容为“我们学院的一位同伴,非常年轻……,但却是一位具有非凡天赋和卓越才能的人物”。2
1 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 134。
2 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 202。
在本章,我们来考察一下牛顿早期的如下几个成就:将某些表达式转换为无穷级数的广义二项展开式,求无穷级数的逆级数的方法,以及确定曲线之下的面积的求积法则。最后我们介绍一个惊人的结果,即一个角的正弦的级数展开。关于二项展开式的最早描述出现在他回答莱布尼茨询问的《前信》3中,那是在他完成最初的研究工作很久以后。本章其他素材来自牛顿1669年的论著《运用无穷多项方程的分析学》,这本著作通常简称为《分析学》。
3 为答复莱布尼茨的有关询问,牛顿在1676年先后两次致信英国皇家学会秘书H.奥尔登堡,分别称为《前信》和《后信》,在《前信》中追述了对二项式定理的原始推导和思路。——译者注
尽管本章仅限于讨论牛顿早期的工作,但是需要指出,牛顿“早期的工作”几乎总是超越其他任何人深思熟虑的工作。
广义二项展开式
截至1665年,牛顿已经发现将二项式展开(他的说法是“化简”)成级数的简单方法。对他而言,这种化简不仅是用另一种形式重建二项式的手段,同时也是通向流数术的大门。这个二项式定理是牛顿众多数学发明的起点。
正如《前信》所述,眼前的问题是化简二项式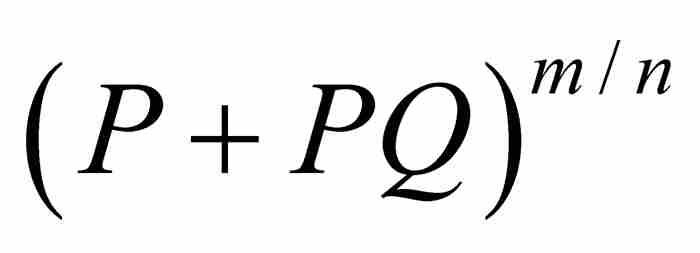 ,而不管m/n“是整数还是分数,或者是正数还是负数”。1 在人们对指数还非常生疏的时代,这本身是一个非常大胆的思想,那时牛顿首次强调“用
,而不管m/n“是整数还是分数,或者是正数还是负数”。1 在人们对指数还非常生疏的时代,这本身是一个非常大胆的思想,那时牛顿首次强调“用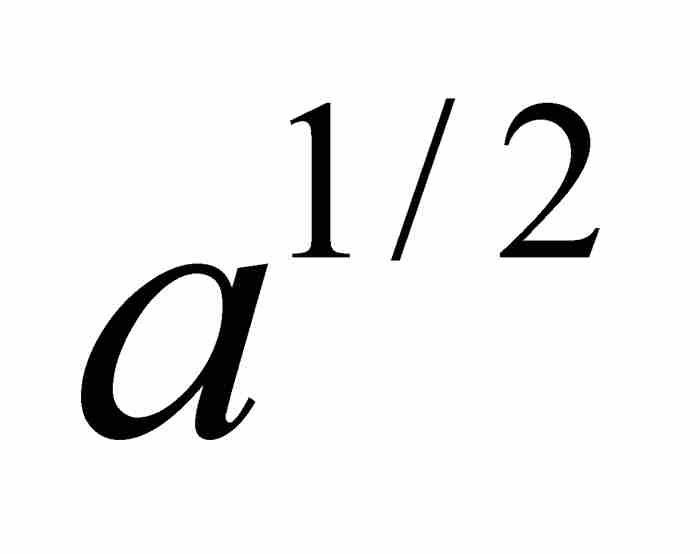 ,
,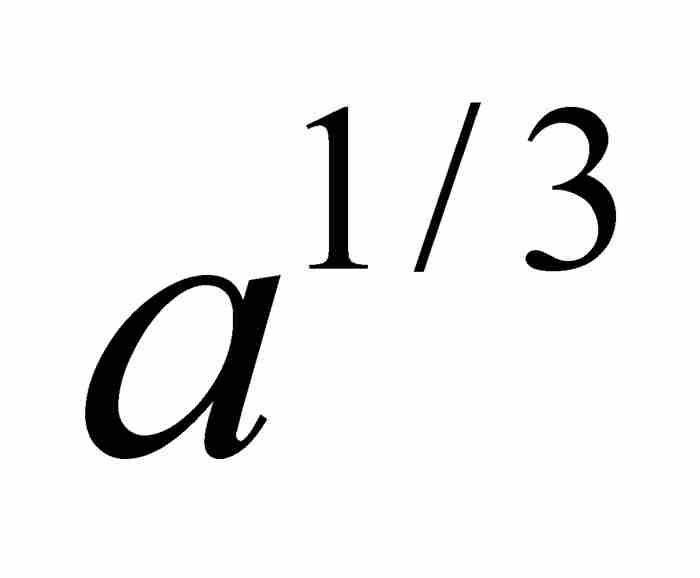 ,
,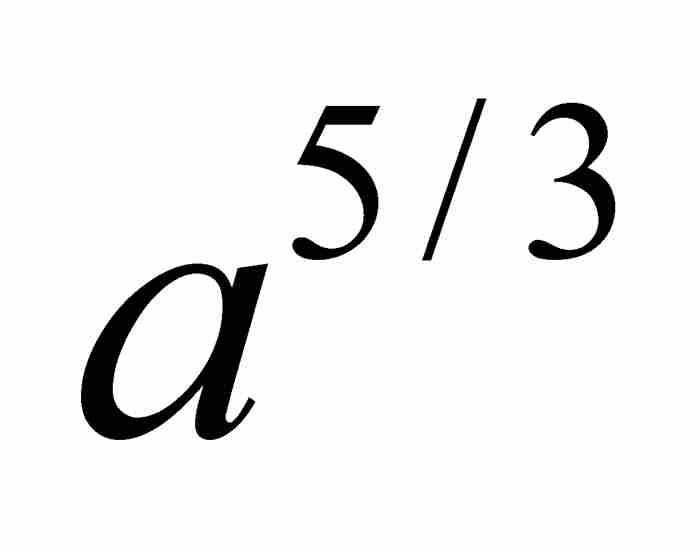 代替
代替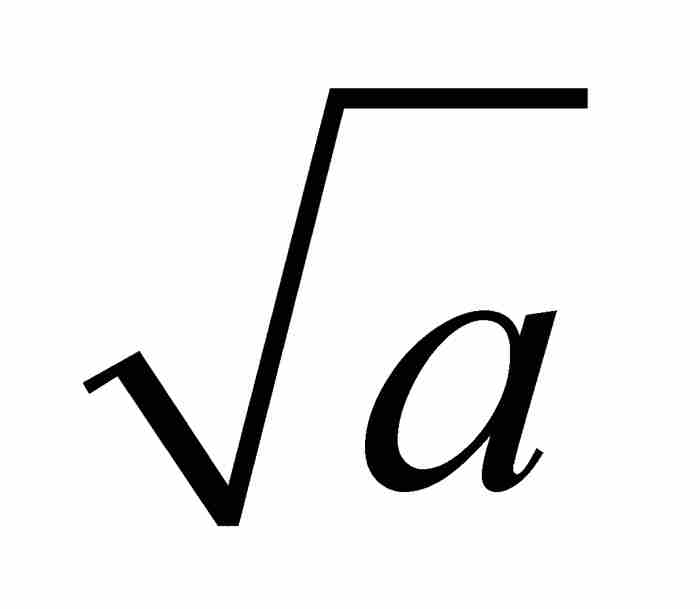 ,
,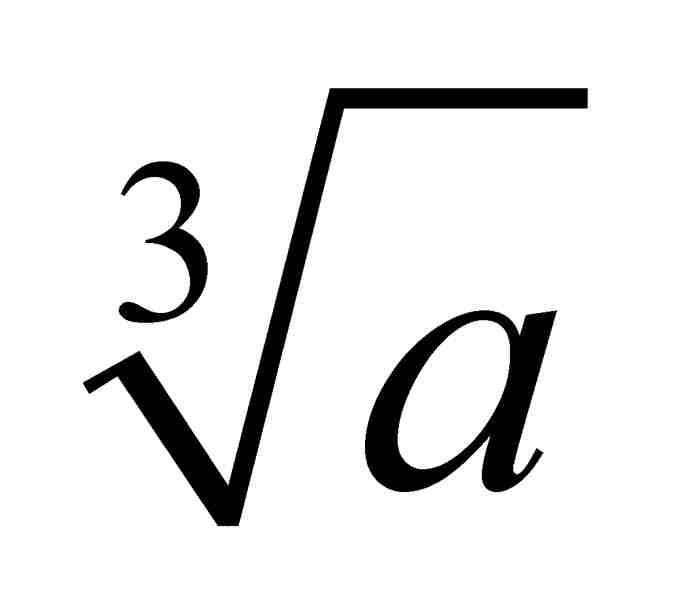 ,
,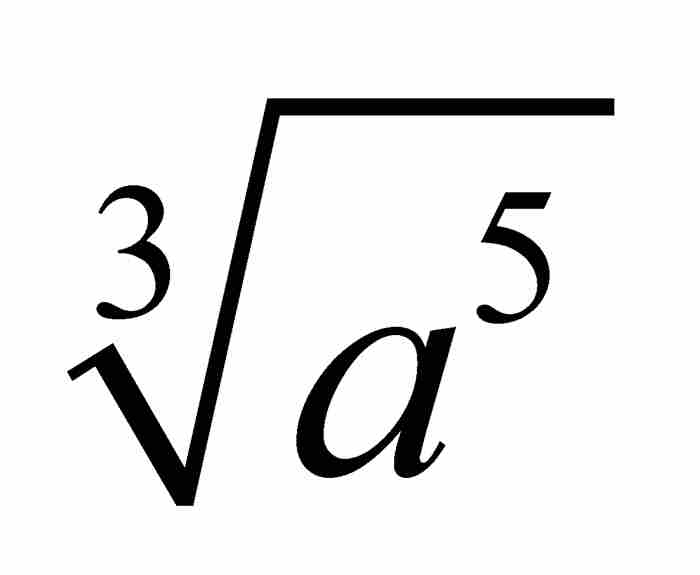 , 用
, 用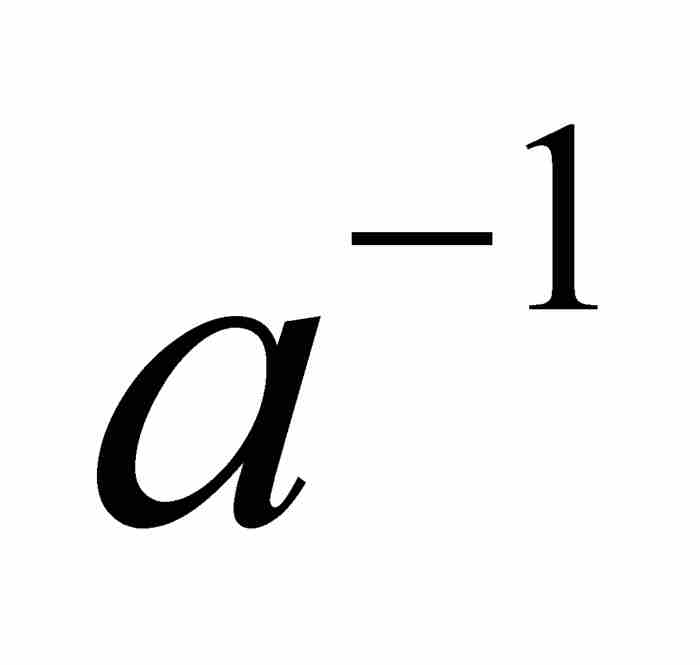 ,
,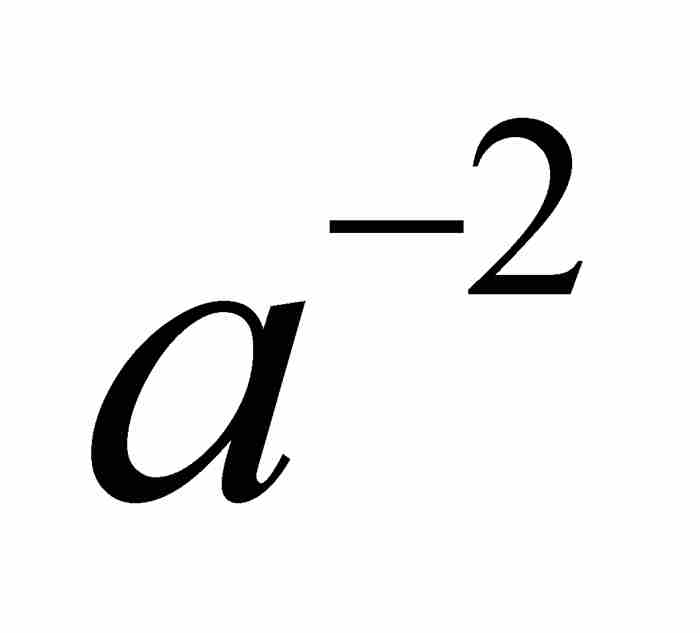 ,
,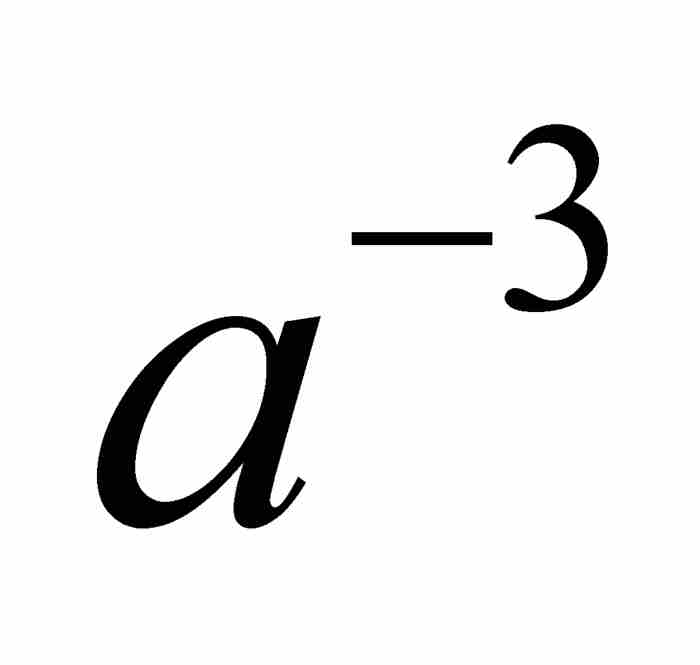 代替
代替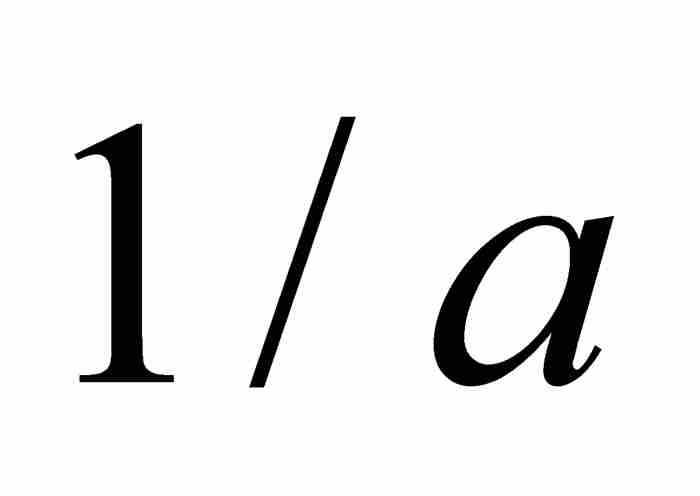 ,
,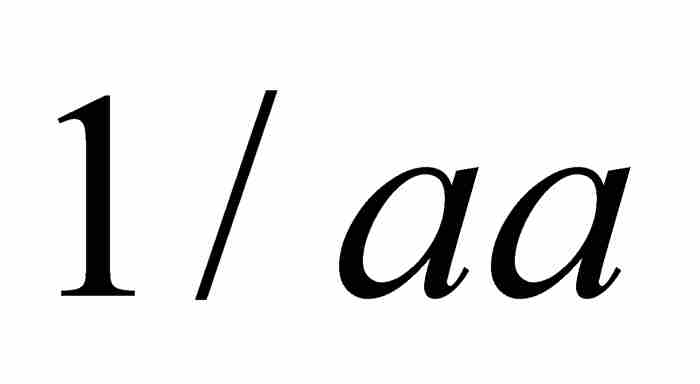 ,
,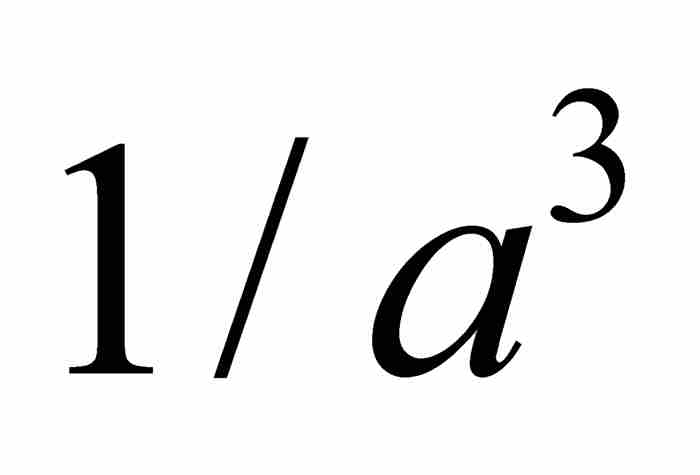 ”。2 显然,当时的读者需要适当的提示。
”。2 显然,当时的读者需要适当的提示。
1 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard Vniversity Press, 1969, p. 286。
2 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard Vniversity Press, 1969, p. 286。
牛顿不但发现了像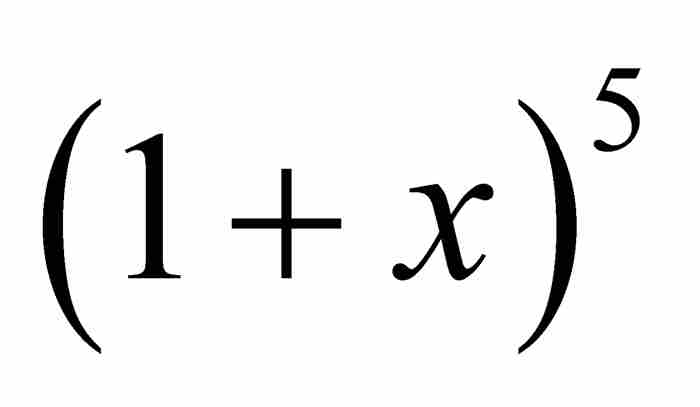 这样基本的二项式的展开形式,而且发现了像
这样基本的二项式的展开形式,而且发现了像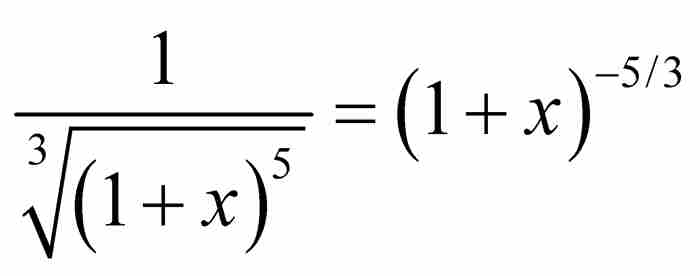 这样复杂的二项式的展开形式。正如牛顿向莱布尼茨解释的那样,这种化简服从规则
这样复杂的二项式的展开形式。正如牛顿向莱布尼茨解释的那样,这种化简服从规则
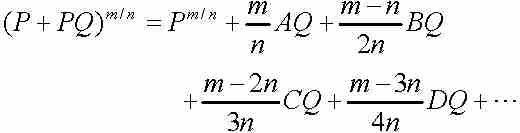 (1)
(1)
其中A,B,C, …分别代表前一项,我们将在下面举例说明。这就是著名的牛顿二项式展开式,虽然这种形式或许是新奇的。
牛顿给出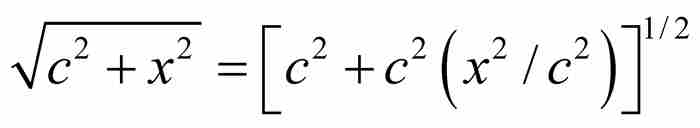 的例子。在这个例子中
的例子。在这个例子中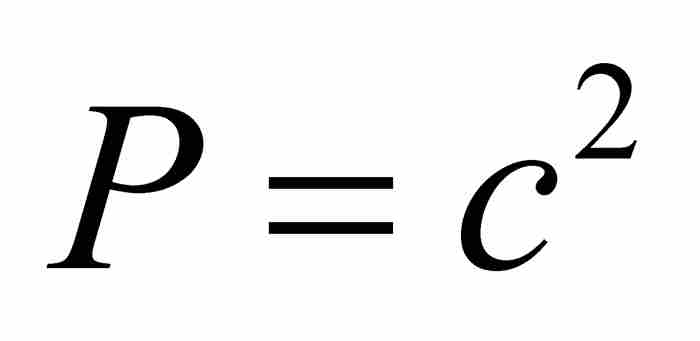 ,
,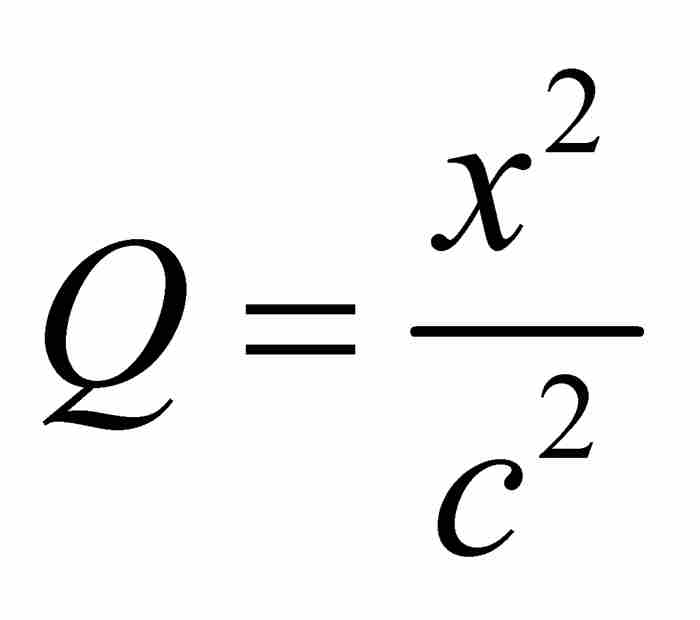 ,
,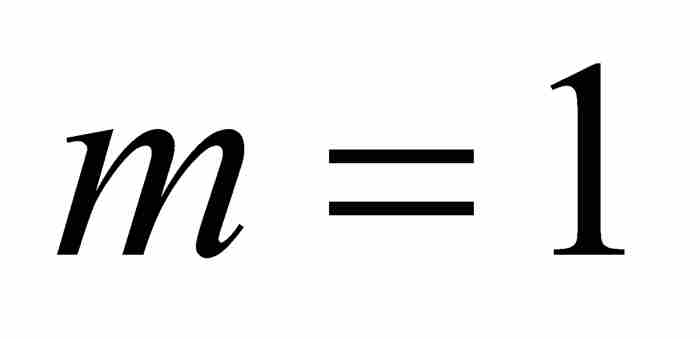 ,
,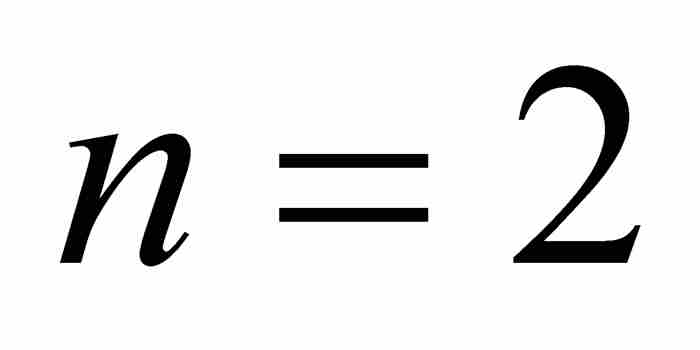 。因此,
。因此,
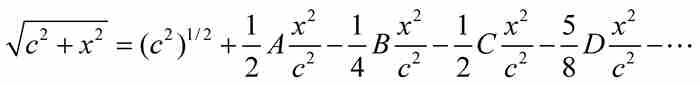
为了确定A, B, C及其他系数,我们可以利用它们都表示前一项的事实。于是,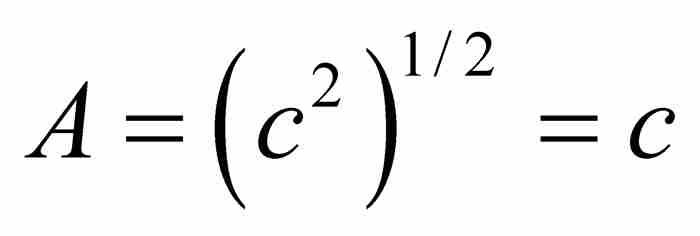 ,给出
,给出
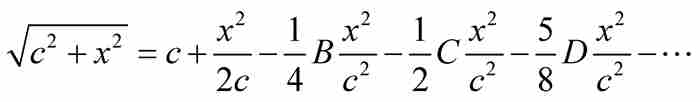
同样,B表示前一项,即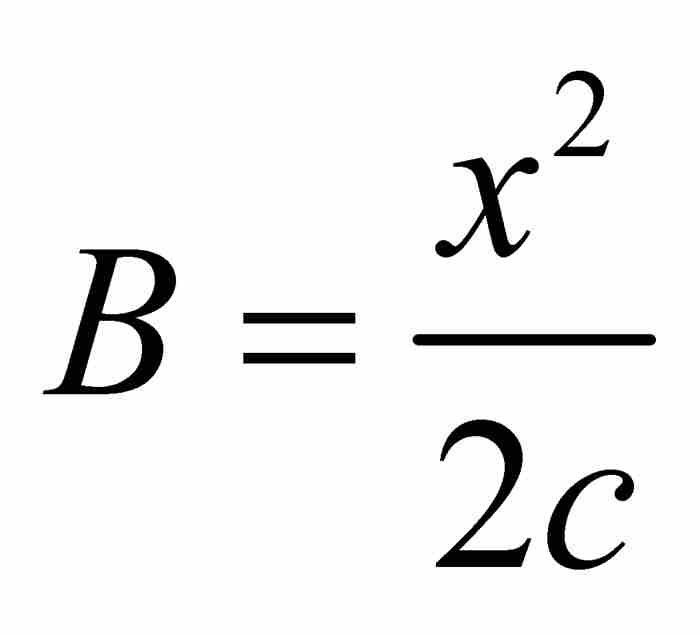 ,由此得到
,由此得到

用类似的代入得到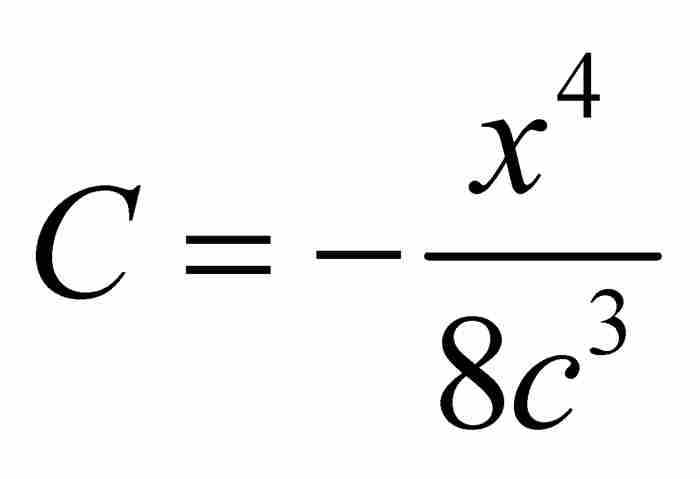 ,然后得到
,然后得到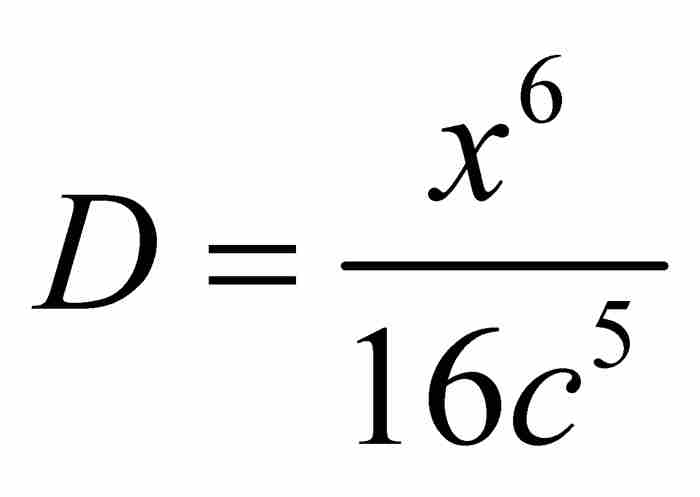 。以这种方式从左到右继续推导,牛顿得到
。以这种方式从左到右继续推导,牛顿得到
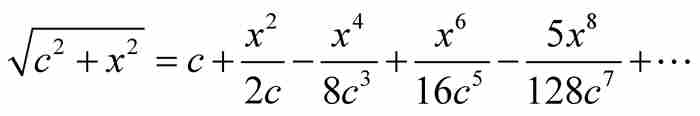
显然,这种方法有一点递归的味道:从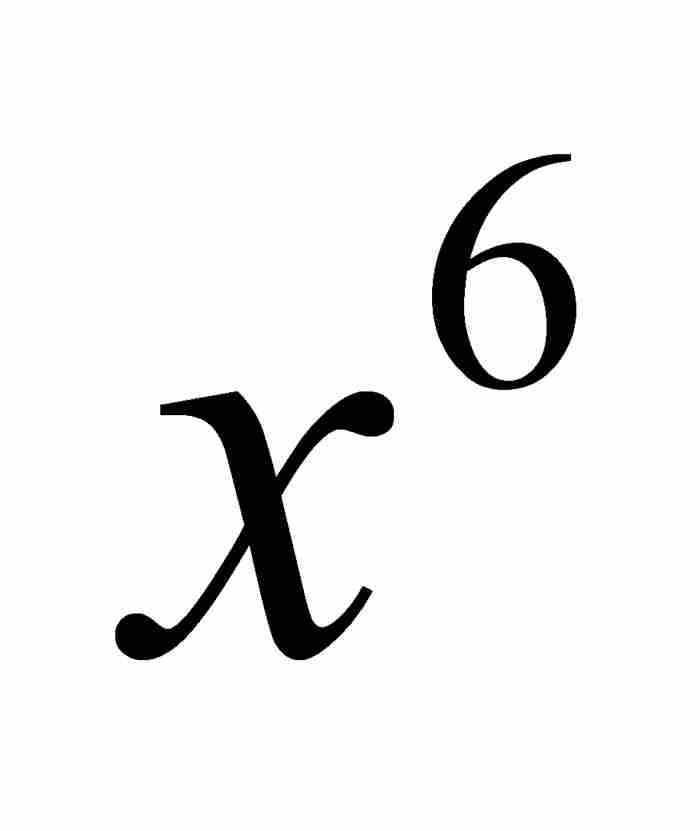 的系数求出
的系数求出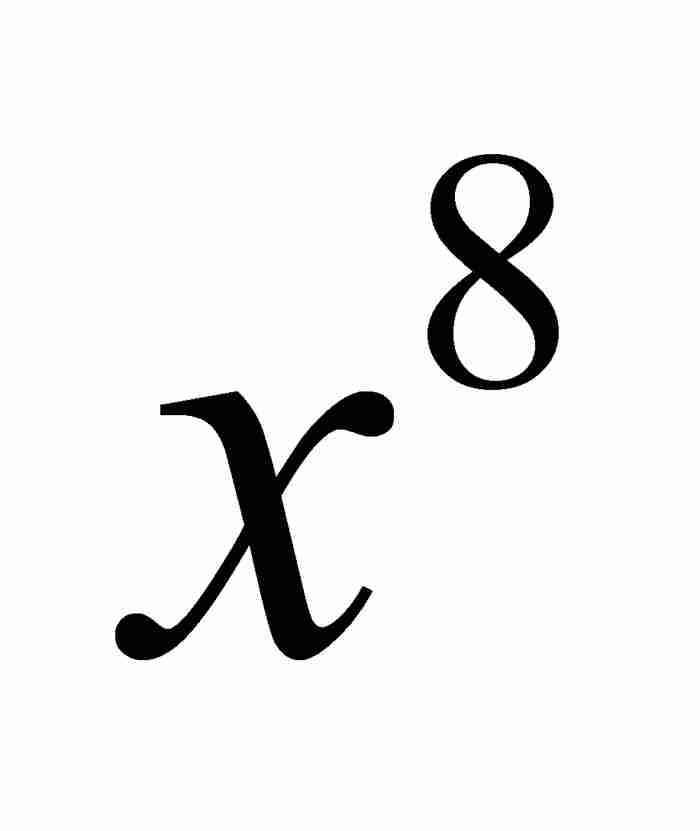 的系数,而欲求
的系数,而欲求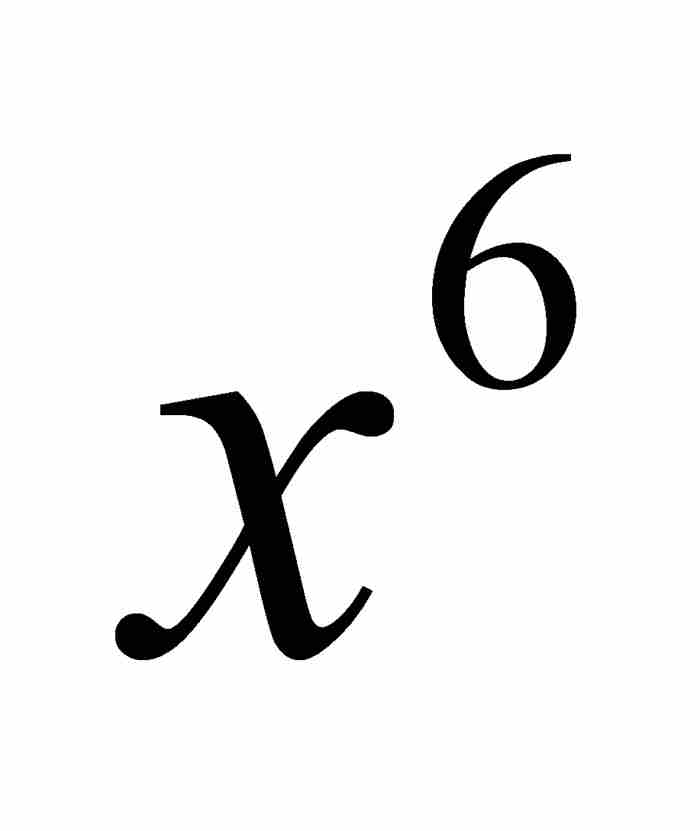 的系数需要知道
的系数需要知道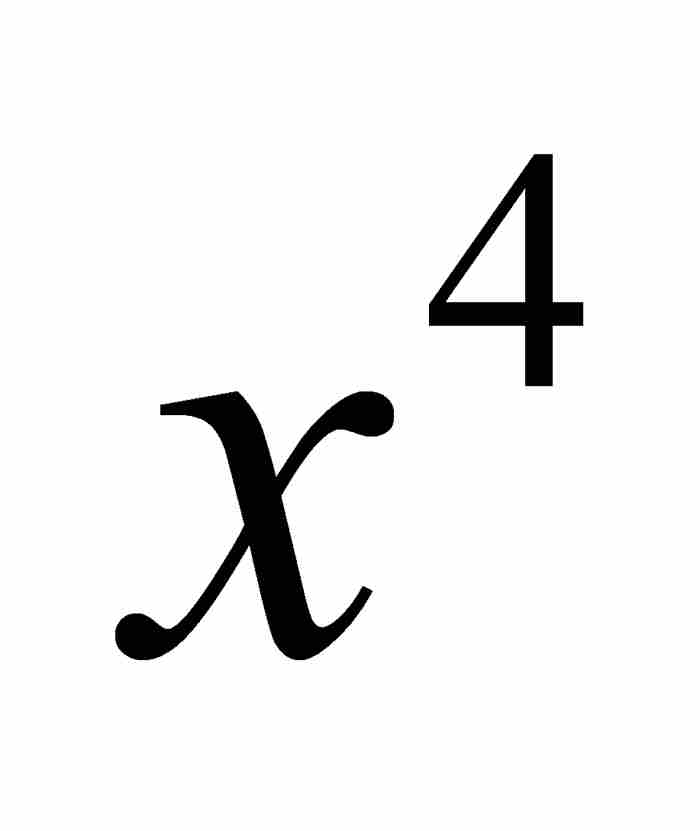 的系数,依此类推。虽然现代的读者可能习惯于二项式定理的直接表述,但是牛顿的递归表示具有无可争辩的吸引力,因为当用前一项来计算后一项的数值系数时,可以使计算过程得以简化。
的系数,依此类推。虽然现代的读者可能习惯于二项式定理的直接表述,但是牛顿的递归表示具有无可争辩的吸引力,因为当用前一项来计算后一项的数值系数时,可以使计算过程得以简化。
为明确起见,简单的方法是用由P和Q表示的A, B, C, …的等价表达式代替A, B, C, …,然后约去式(1)两端的公因子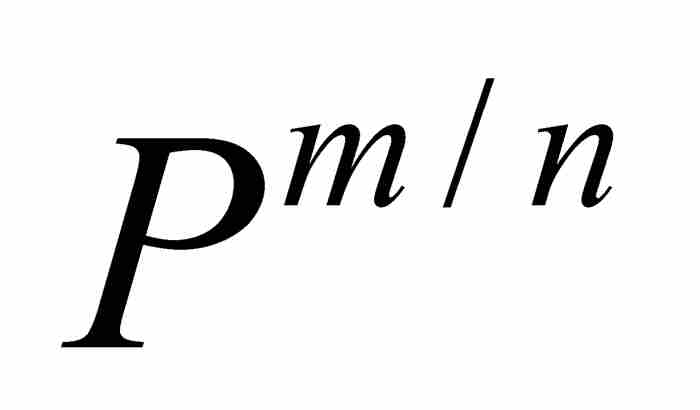 ,就获得现在的公式:
,就获得现在的公式:
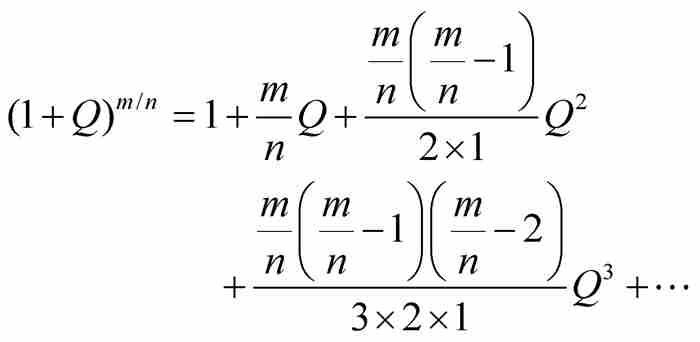
(2)
牛顿将这种简化比作是从平方根到无穷小数的转换,并且不遗余力地推崇这一运算的好处。他在1671年写道:
这是一种产生无穷级数的简便方法,所有复杂的项……都可以简化为一类简单的量,即分子和分母都是简单项的分数的无穷级数,这样将会消除那些其原始形式看起来几乎难以逾越的困难。3
3 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 37。
的确,将数学家从不可逾越的难题中解脱出来是一件值得做的事情。
再举一个有助于理解的例子——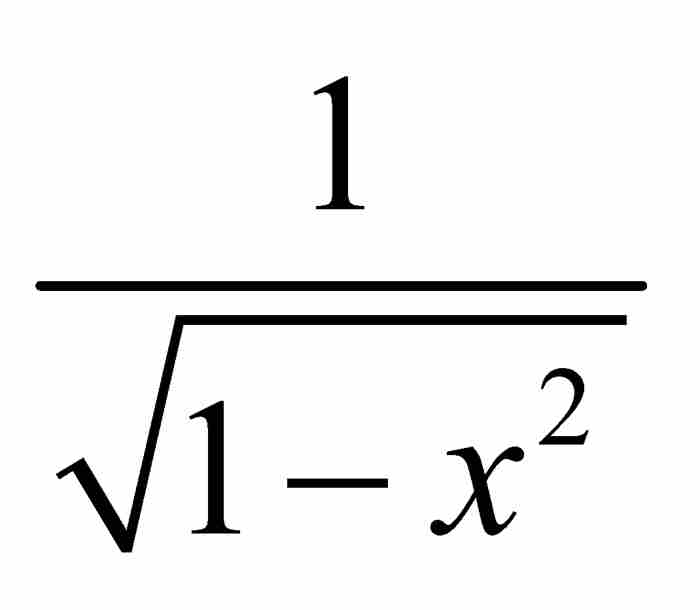 的展开式,在本章后面将要讨论的一个结果中,将会展示牛顿对这个展开式的巧妙应用。我们首先将上式写成
的展开式,在本章后面将要讨论的一个结果中,将会展示牛顿对这个展开式的巧妙应用。我们首先将上式写成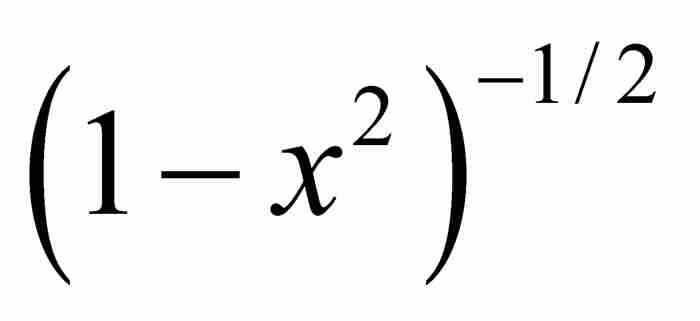 ,确定
,确定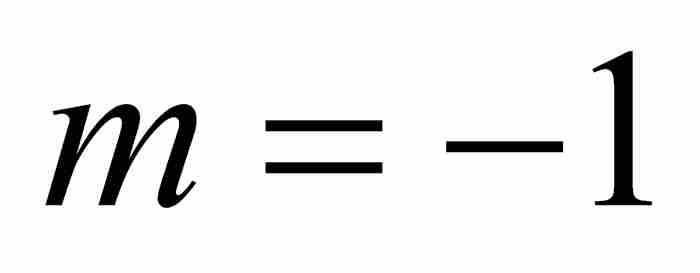 ,
,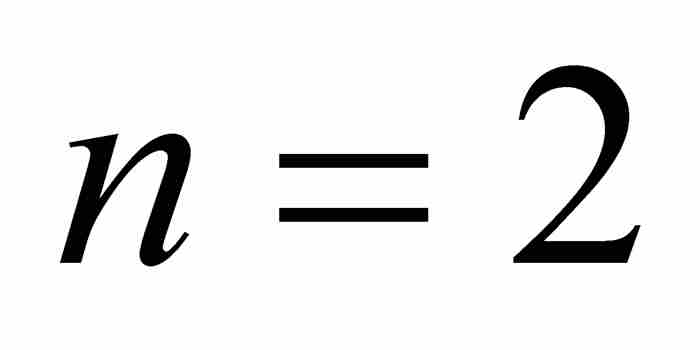 ,
,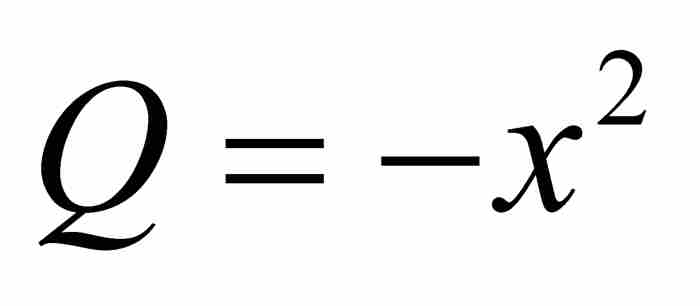 ,并利用式(2):
,并利用式(2):
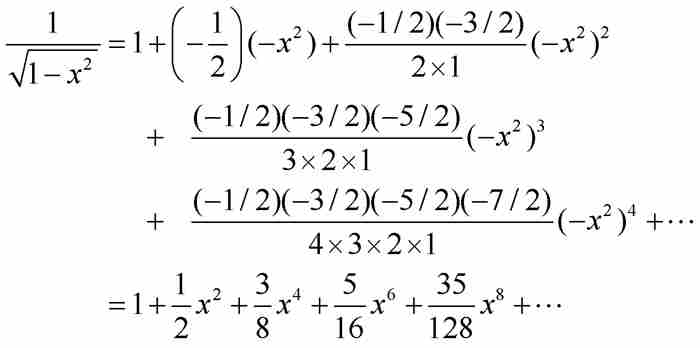
(3)
牛顿通过将级数平方并检查其结果来“检验”式(3)这样的展开式。如果我们也这样做,并且限制取次数不超过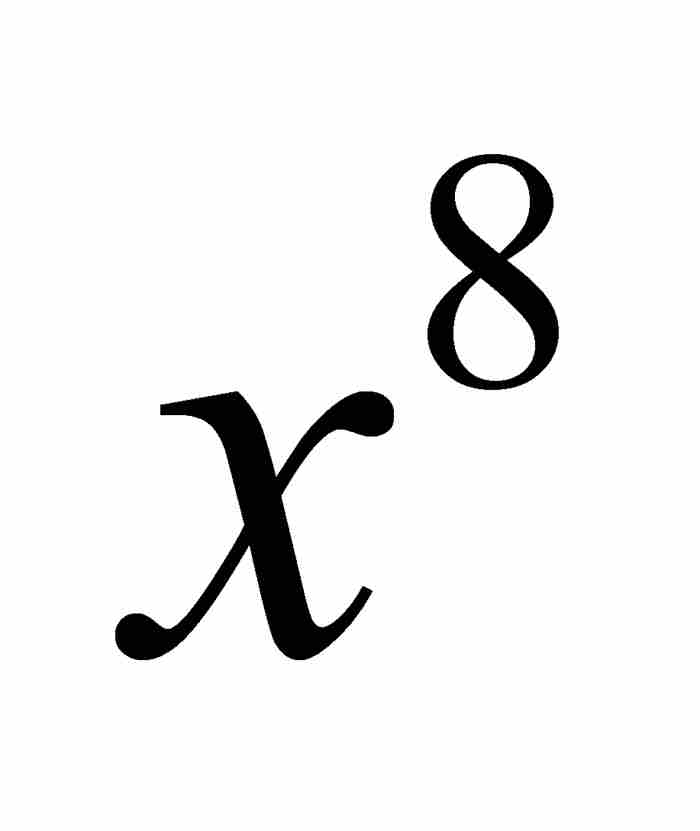 的项,得到
的项,得到
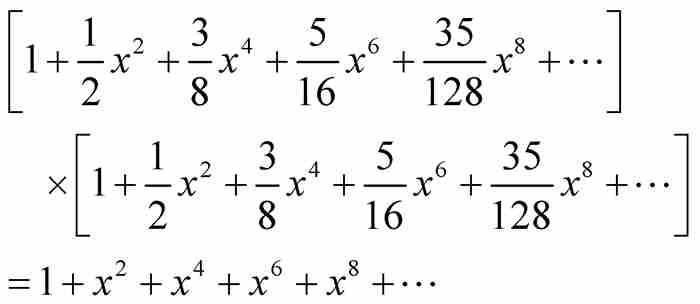
其中全部系数奇迹般地变成了1(读者不妨试试吧!)。自然,得到的乘积是公比为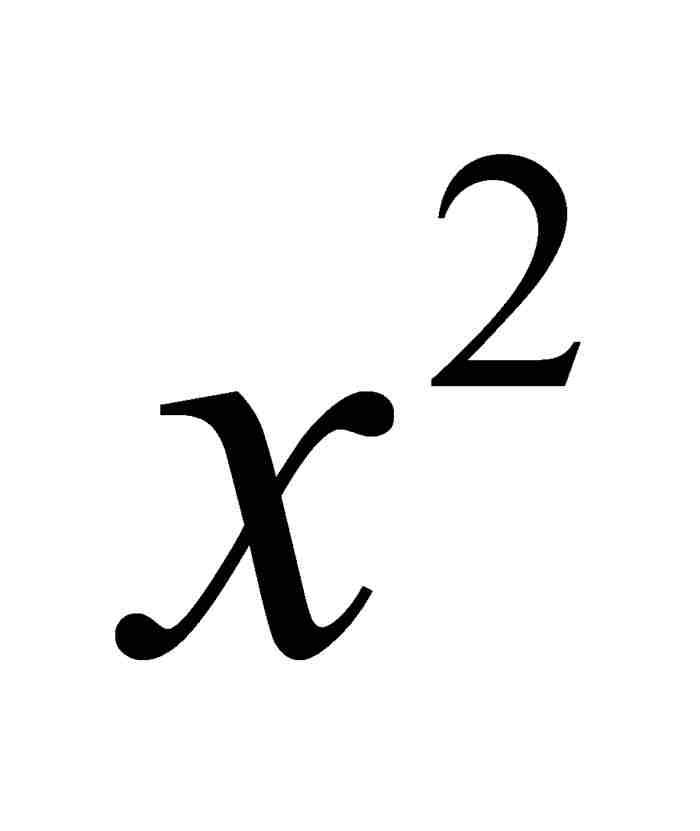 的无穷等比级数,由已有的公式可知,其和为
的无穷等比级数,由已有的公式可知,其和为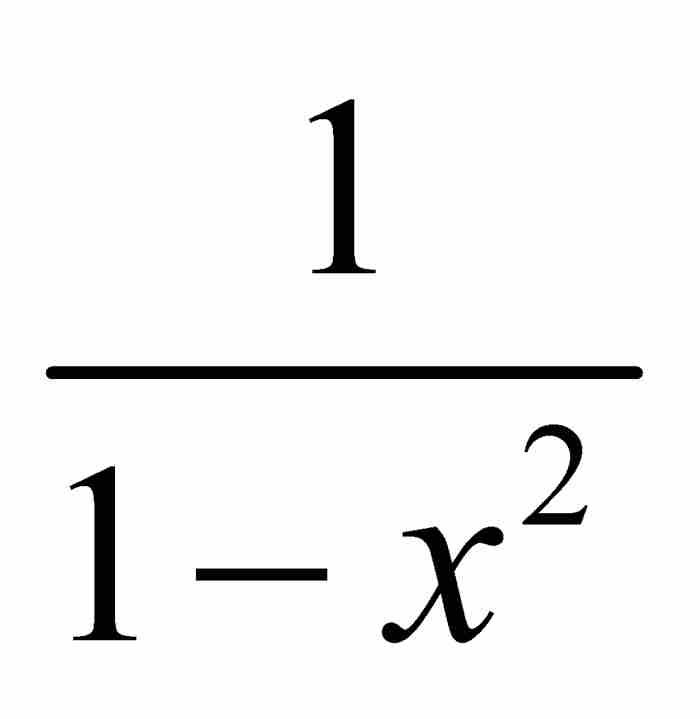 。但是,如果级数(3)的平方为
。但是,如果级数(3)的平方为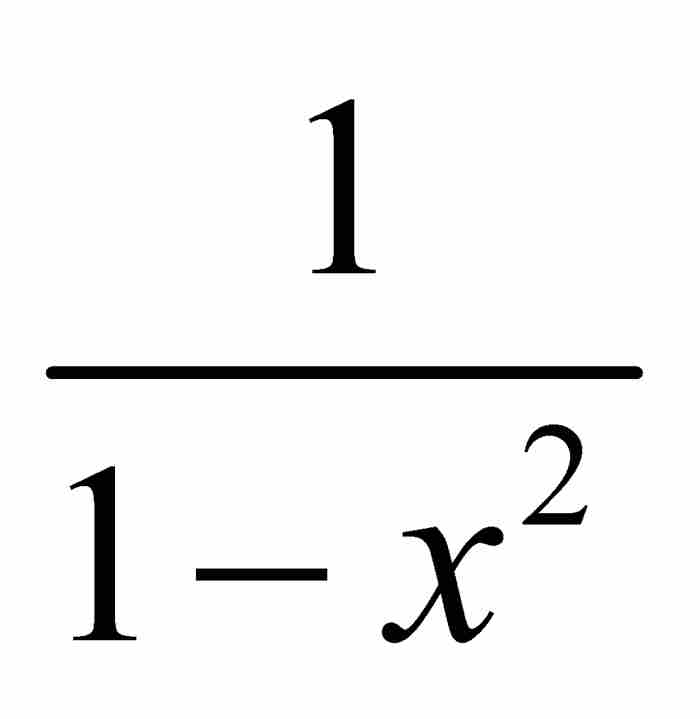 ,那么,我们推断级数本身必定是
,那么,我们推断级数本身必定是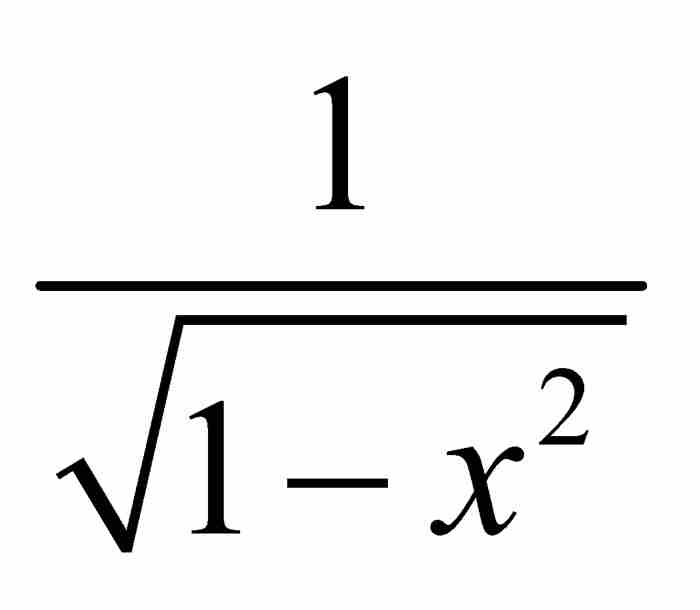 。妙极了!
。妙极了!
牛顿将这样的计算当作让人信服他的普遍性结论的证明。他断言“尽管我们这些凡人的推理能力非常有限,既不能表达也不能想象这些等式的所有项,就像我们无法确切知道那些量从何而来一样”,但是“可以把对有限项等式的一般分析”推广到这样的无限项表达式。4
4 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 22。
逆级数
在描述把某些二项式化简为形如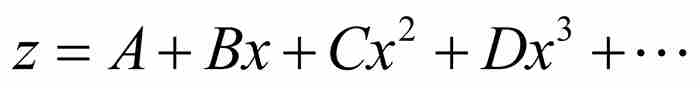 的无穷级数的方法以后,牛顿进一步寻找通过z的项把x表示成级数的方法。用现在的术语,他是寻找逆级数关系。所得到的方法对代数学并未产生显著影响,但是随后将会看到,我们对它的关注是正确的。像牛顿的做法一样,我们通过一个特例来描述求逆级数的过程。
的无穷级数的方法以后,牛顿进一步寻找通过z的项把x表示成级数的方法。用现在的术语,他是寻找逆级数关系。所得到的方法对代数学并未产生显著影响,但是随后将会看到,我们对它的关注是正确的。像牛顿的做法一样,我们通过一个特例来描述求逆级数的过程。
让我们从级数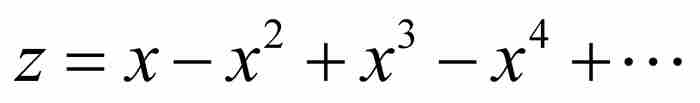 开始,首先将它改写为
开始,首先将它改写为
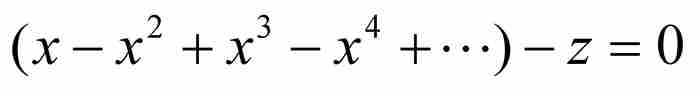 (4)
(4)
并且舍弃所有x的指数大于或等于2的项。自然,这样剩下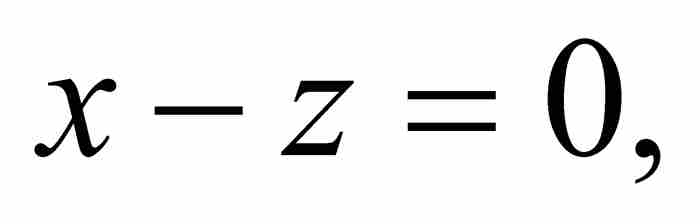 ,从而,逆级数开始于
,从而,逆级数开始于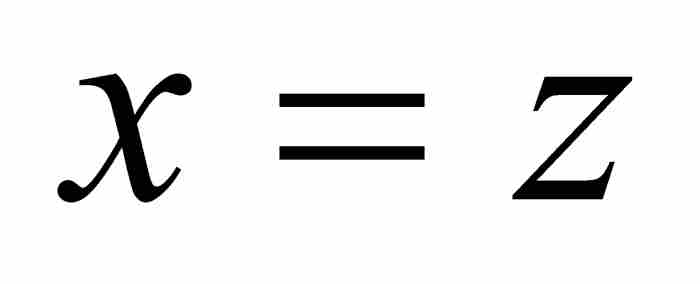 。
。
牛顿认识到舍弃全部高阶项会导致不准确的解。准确的答案应该具备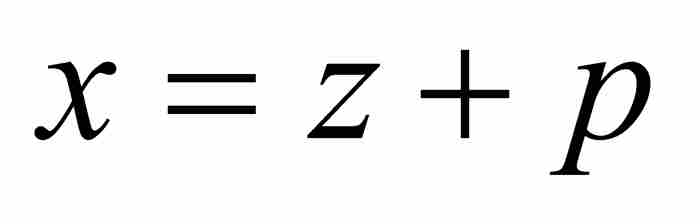 的形式,其中p是有待确定的级数。在式(4)中,用
的形式,其中p是有待确定的级数。在式(4)中,用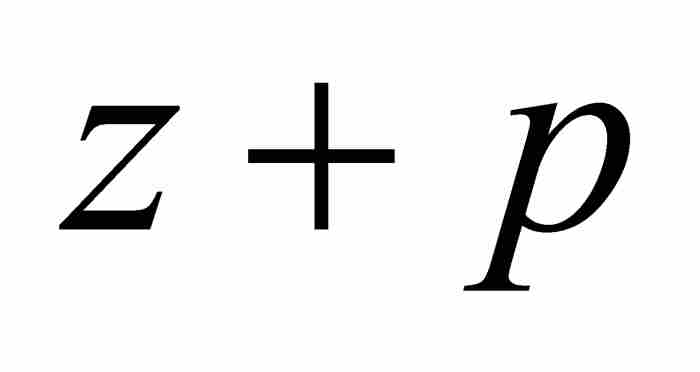 代换x,得到
代换x,得到
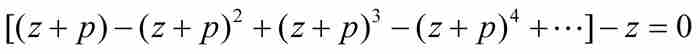
将上式展开并整理后,得到
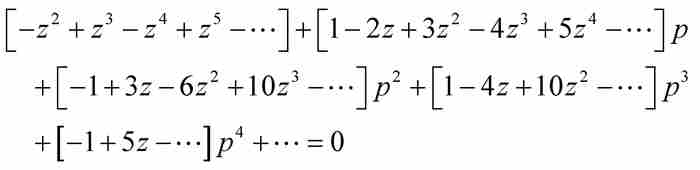 (5)
(5)
下一步,舍弃p的2次方项、3次方项和更高次方项,再求解,得到
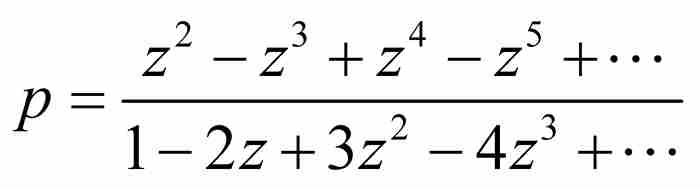
现在,牛顿实施第二轮删除,舍弃分子和分母中除去z的最低次方项以外的所有z的高次方项。由此,p近似等于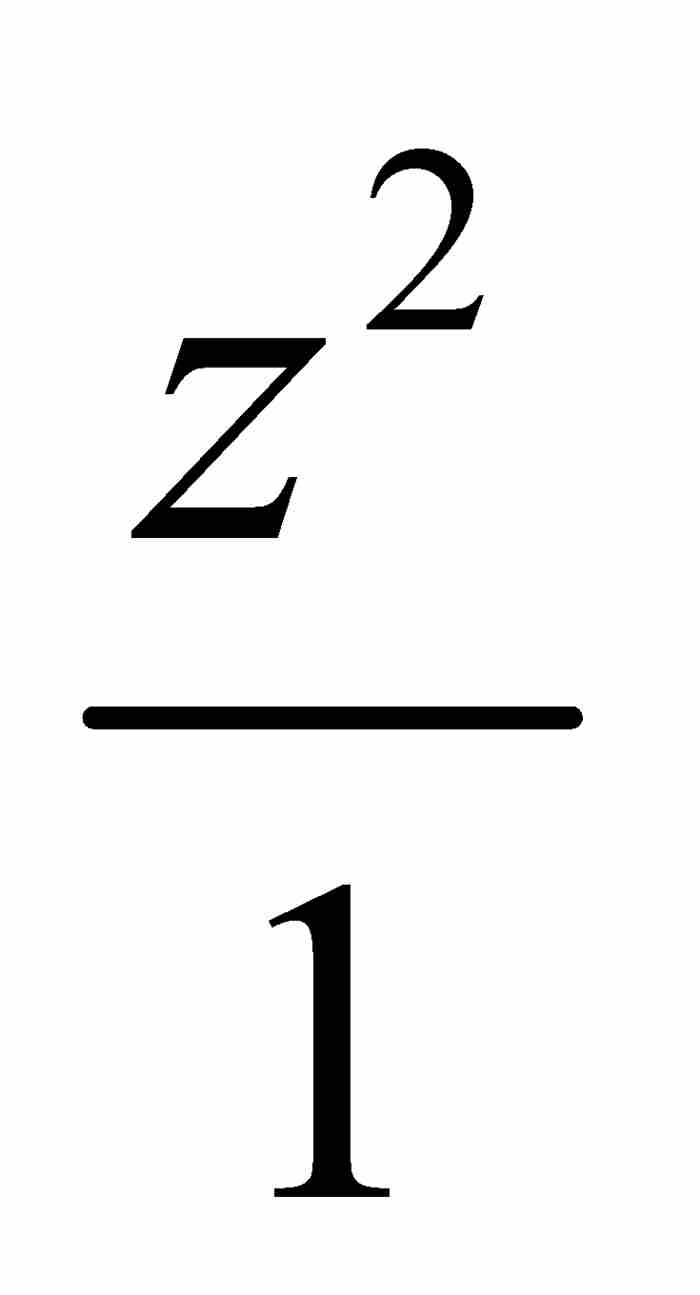 ,所以,到这一步逆级数表示为
,所以,到这一步逆级数表示为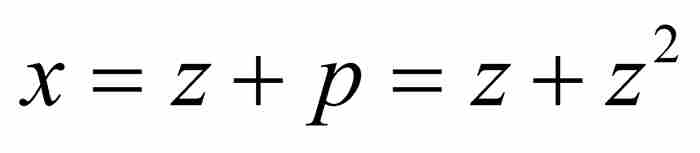 。
。
但是p并非恰好等于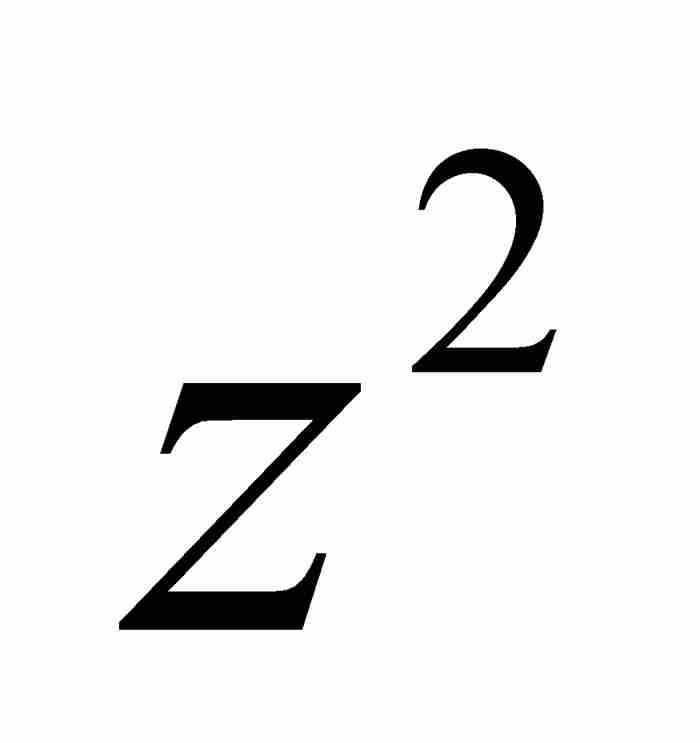 。更准确地说,
。更准确地说,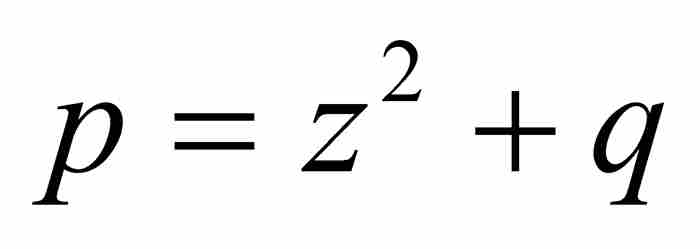 ,其中q是有待确定的级数。为求出q,我们将其代入式(5),得到
,其中q是有待确定的级数。为求出q,我们将其代入式(5),得到
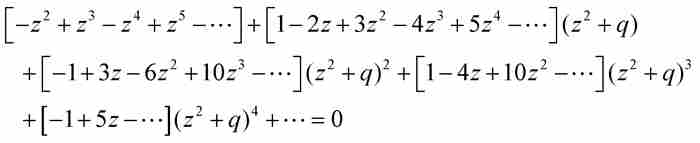
展开并按q的乘方合并同类项,得到
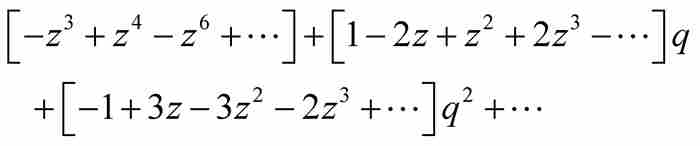 (6)
(6)
同前面一样,舍弃q的高于1次方的项,求解得到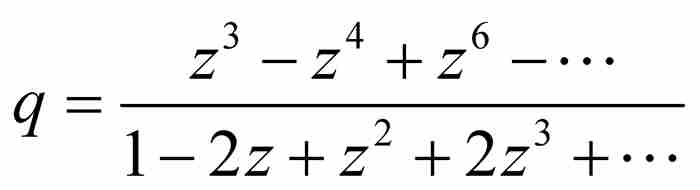 ,然后舍弃分子分母中除去z的最低次方项以外的所有项,得到
,然后舍弃分子分母中除去z的最低次方项以外的所有项,得到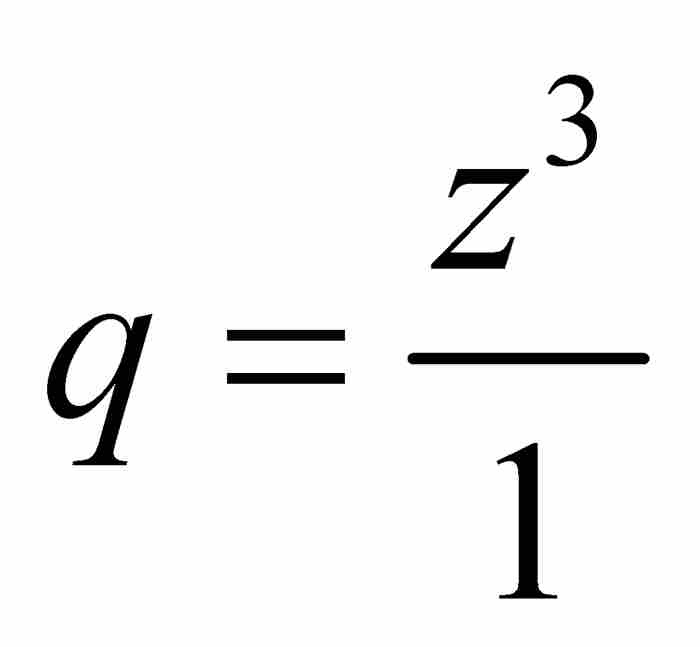 。至此,级数的形式变成了
。至此,级数的形式变成了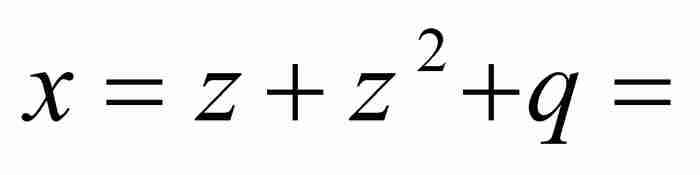
 。
。
将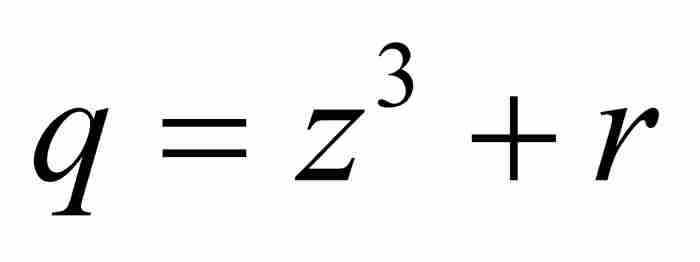 代入式(6),可以继续这一推导过程。对于代数的单调乏味有着非凡忍耐力的牛顿似乎可以将这样的计算(几乎)无限地延续下去。但是,牛顿最终也乐于回过头来审视结果,寻找某种一般的表达形式。牛顿这样写道:“让考察停留在这里,顺便指出,当第5项或者第6项……为已知时,如果愿意的话,一般来说,通过观察这一过程的相似性,可以把推导随意进行下去”。1
代入式(6),可以继续这一推导过程。对于代数的单调乏味有着非凡忍耐力的牛顿似乎可以将这样的计算(几乎)无限地延续下去。但是,牛顿最终也乐于回过头来审视结果,寻找某种一般的表达形式。牛顿这样写道:“让考察停留在这里,顺便指出,当第5项或者第6项……为已知时,如果愿意的话,一般来说,通过观察这一过程的相似性,可以把推导随意进行下去”。1
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 20。
对于我们的例子,这种考察表明,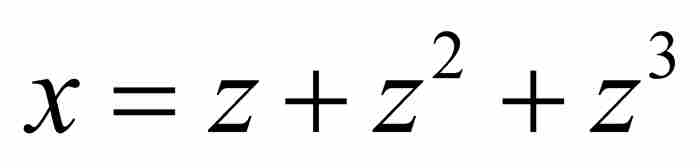
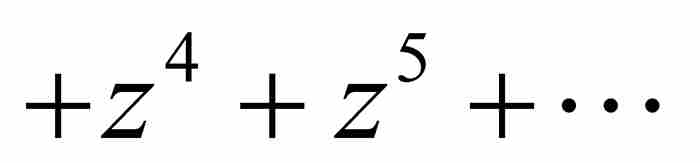 是我们开始时的级数
是我们开始时的级数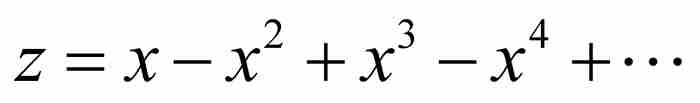 的逆级数。
的逆级数。
这个结果在什么意义上是可靠的?毕竟,牛顿多次舍弃了绝大多数项,所以,这个答案的正确性还有多大的可信度呢?
下面的“检验”再次让我们安心。原来的级数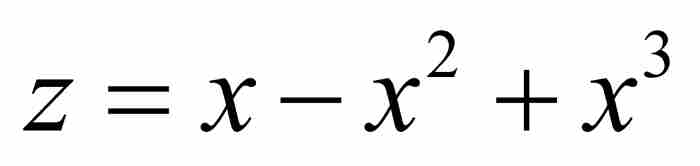
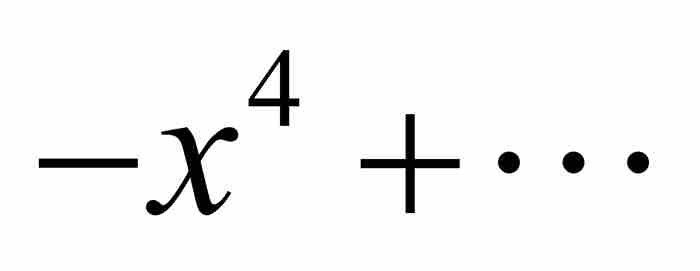 是公比为
是公比为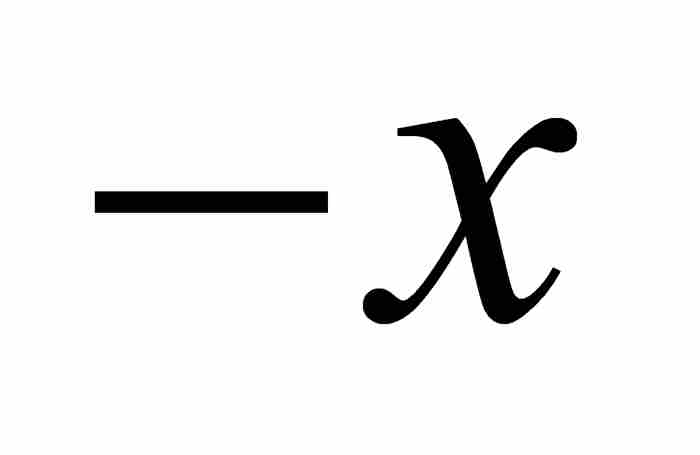 的等比级数,所以它的终极形式为
的等比级数,所以它的终极形式为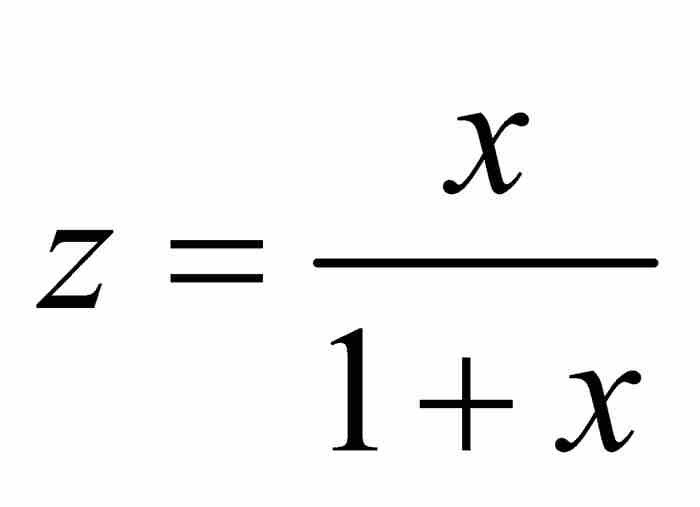 。因此,我们看出
。因此,我们看出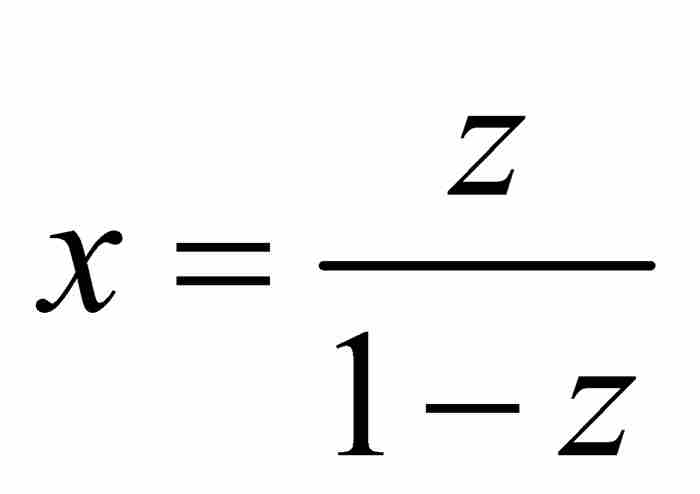 是等比级数
是等比级数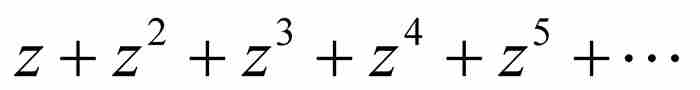 的和。这恰好是牛顿的推导过程给出的结果。一切推导看起来是有条不紊的。
的和。这恰好是牛顿的推导过程给出的结果。一切推导看起来是有条不紊的。
到目前为止,所讨论的方法(广义二项展开式和逆级数)将成为牛顿手中强有力的工具。然而,在我们真正评价这位大师的成果之前,还有最后一项必备知识。
《分析学》中求面积的法则
牛顿在1669年所写的《分析学》一书中,承诺要论述求面积的方法,“我在很早以前已经发明了通过无穷项级数来计算曲线之下面积的方法”。1 这不是牛顿第一次提到他的流数发明,他在1666年10月撰写的一本小册子《流数简论》中就说过同样的话。《分析学》对那本小书做了修订,展示了这位正在走向成熟的思想家的超人智慧。当代学者发现了一个奇特的现象:除了几位幸运的同事外,神秘的牛顿没有对公众公开这份手稿。直到1711年,其中的许多结果已经由其他人发表之后,这份手稿才印制成书。虽然如此,更早的写作年代和杰出的作者身份表明有理由把本书描绘为“也许是牛顿所有数学著作中最值得称赞的”。2
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 3。
2 Derek Whiteside (ed.), Mathematical Papers of Isaac Newton, vol. 2,Cambridge University Press, 1968, p. 206。
该书以求“简单曲线的面积”的三条法则的一个命题开始。在17世纪,英语中积分(quadrature)的含义是求面积,所以,这三条法则就是积分法则。
法则 1 简单曲线的面积:如果
是曲线AD的函数,其中a是常数,m和n是正整数,那么,区域ABD的面积为
(见图1-1)。
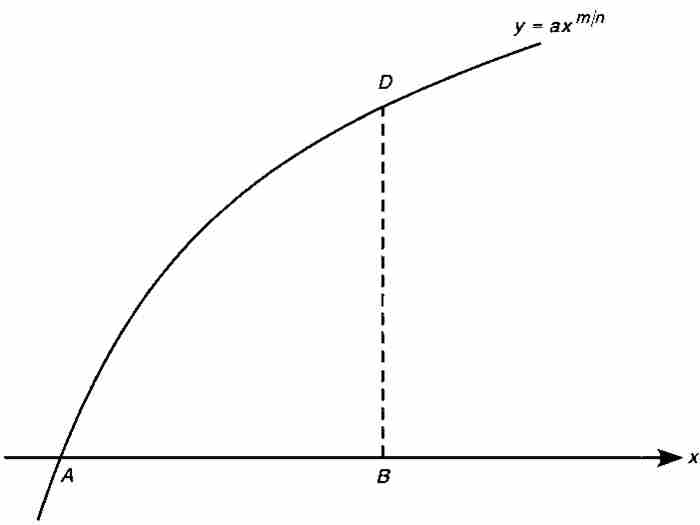
图 1-1
这条法则的一种现代表述形式是,指定A为原点,B为(x, 0),曲线为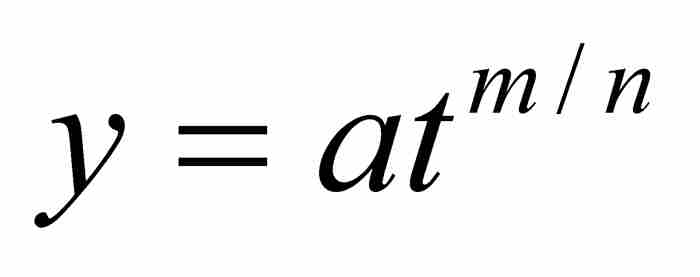 。于是,牛顿的命题变成
。于是,牛顿的命题变成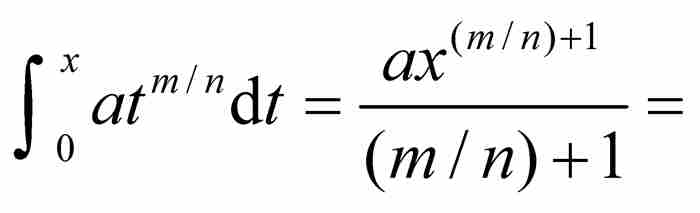
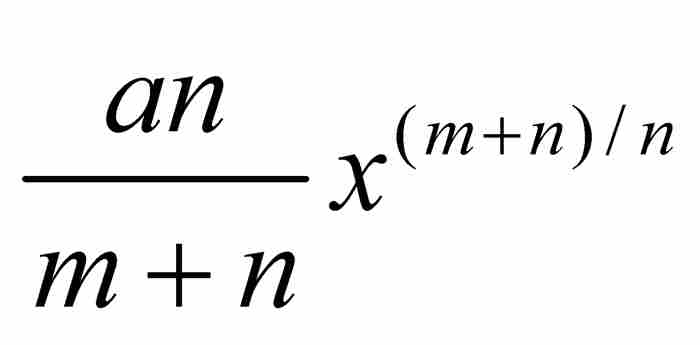 ,这正好是积分学中指数法则的一个特例。
,这正好是积分学中指数法则的一个特例。
仅仅到了《分析学》一书的最后,牛顿几乎像事后反思一样才注意到“留心的读者”会想看到法则1的证明。3留心的读者总是不乏其人的,所以我们在下面给出他的论证。
3 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 22。
如图1-2所示,再次令曲线为AD以及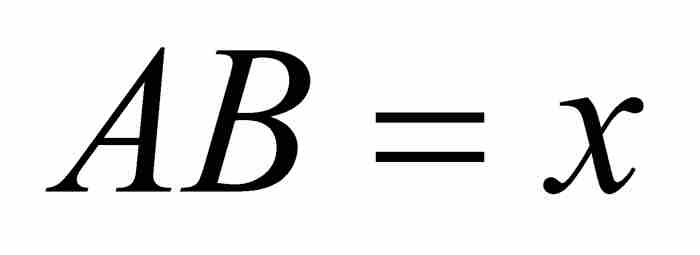 和
和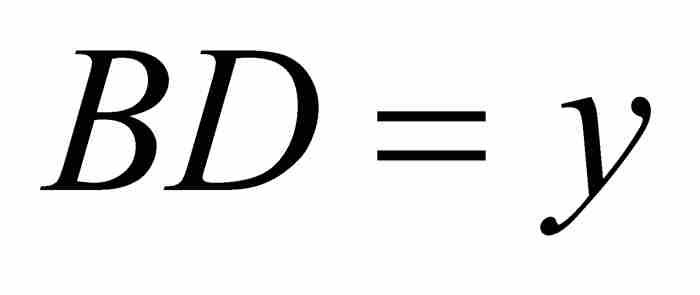 。牛顿假设曲线下的面积 ABD由z通过x的项的表达式给出。目标是求出y通过x表示的对应公式。按照一种现代的居高临下的观点,牛顿是从
。牛顿假设曲线下的面积 ABD由z通过x的项的表达式给出。目标是求出y通过x表示的对应公式。按照一种现代的居高临下的观点,牛顿是从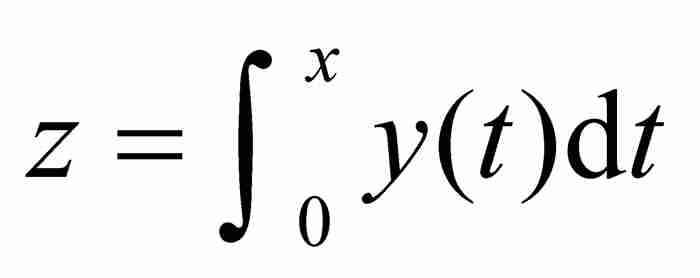 开始求解
开始求解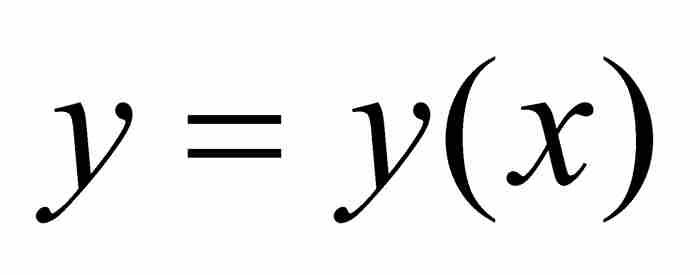 。在以几个戏剧性的步骤结束之前,牛顿的推导过程综合了几何、代数和流数的方法。
。在以几个戏剧性的步骤结束之前,牛顿的推导过程综合了几何、代数和流数的方法。
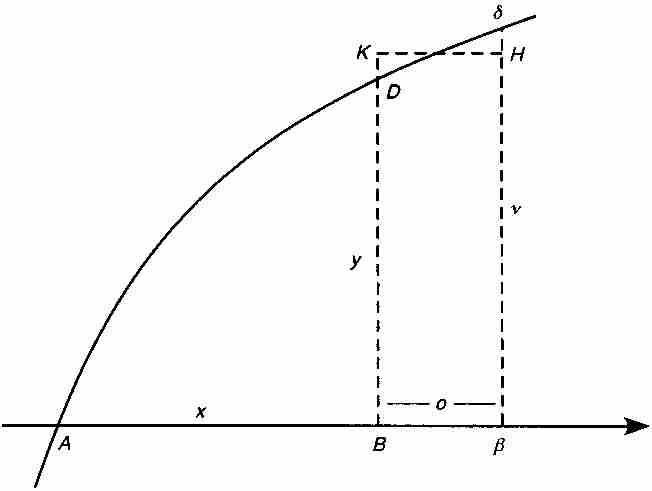
图 1-2
首先,牛顿令β是横坐标轴上同B相隔一小段距离o的点。因此线段Aβ的长度为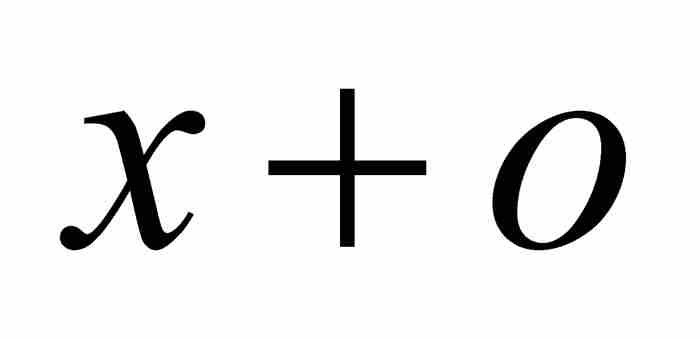 。他令z为面积ABD,不过为强调函数关系,我们有权用
。他令z为面积ABD,不过为强调函数关系,我们有权用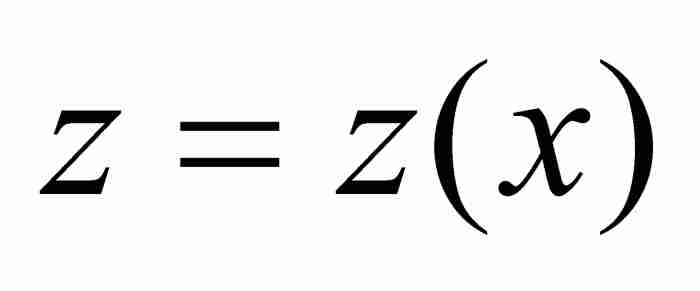 表示。因此,
表示。因此,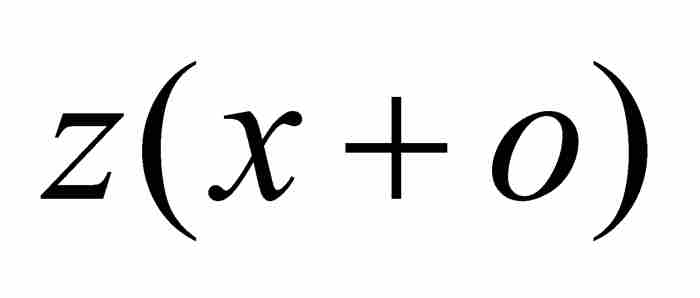 是曲线下的面积Aβδ。下一步,他引进高为v=BK=βH的矩形BβHK,他限定其面积恰好等于曲线下面的区域BβδD的面积。换句话说,BβδD的面积等于ov。
是曲线下的面积Aβδ。下一步,他引进高为v=BK=βH的矩形BβHK,他限定其面积恰好等于曲线下面的区域BβδD的面积。换句话说,BβδD的面积等于ov。
此时,牛顿指定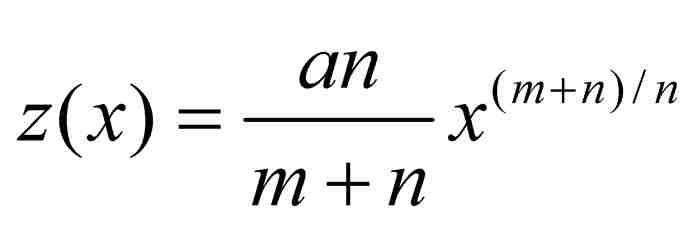 并继续求z的瞬时变化率。为此,他考察了当x变小时x的变化对z的变化的影响。为书写方便,他暂时令
并继续求z的瞬时变化率。为此,他考察了当x变小时x的变化对z的变化的影响。为书写方便,他暂时令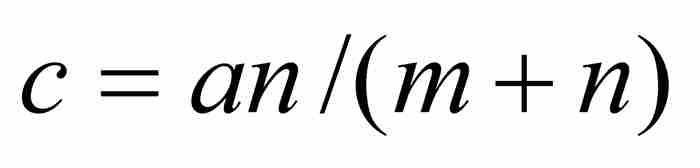 和
和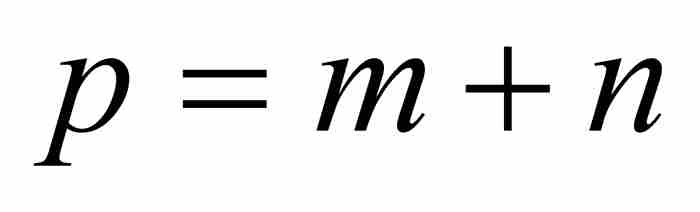 ,于是
,于是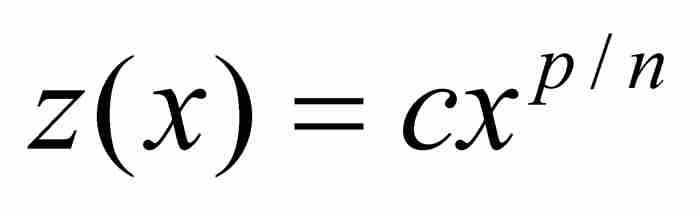 ,且
,且
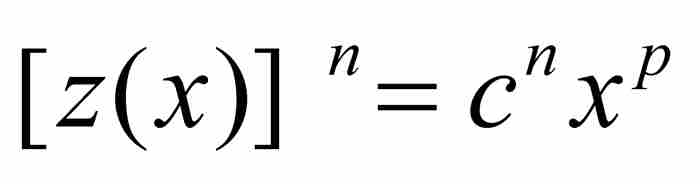 (7)
(7)
现在,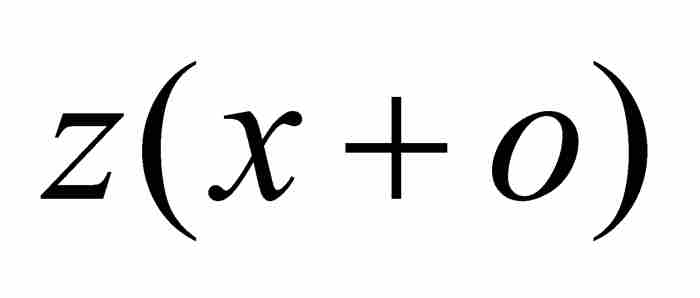 就是面积Aβδ。这个面积可以分解成面积ABD和BβδD。请注意,后者是矩形ov的面积,所以,牛顿断定
就是面积Aβδ。这个面积可以分解成面积ABD和BβδD。请注意,后者是矩形ov的面积,所以,牛顿断定 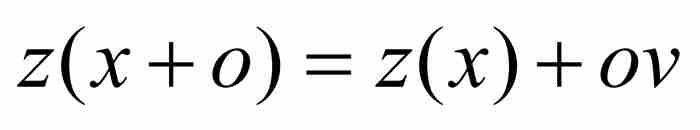 。代入式(7),得到
。代入式(7),得到
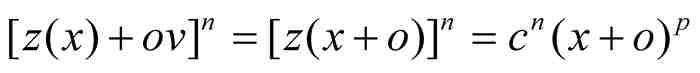
将等式左边的二项式和右边的二项式展开,得到
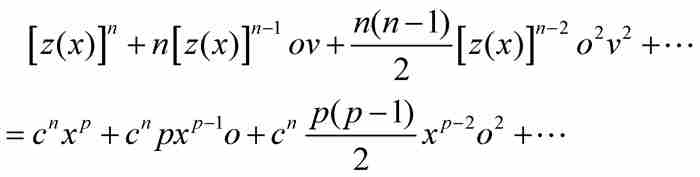
利用式(7)消去等式两边最左边的项,并除以o,牛顿得到
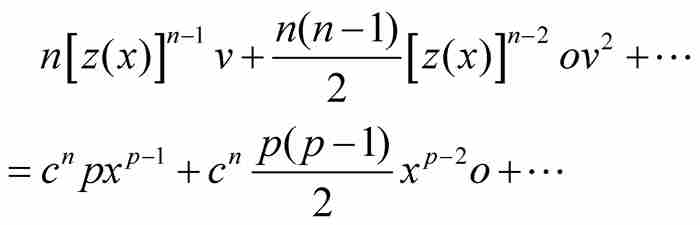 (8)
(8)
到这一步,他写道:“如果我们假定Bβ为无限减小并消失的量,或者o为零,那么,v和y在这种情况下相等,并且那些乘以o的项将消失”。4 他断言,当o变成零时,式(8)中所有包含o的项也变成零。与此同时,v同 y相等,这就是说,图1-2中矩形的高BK将等于原曲线的纵坐标BD。通过这种方式,式(8)变换成
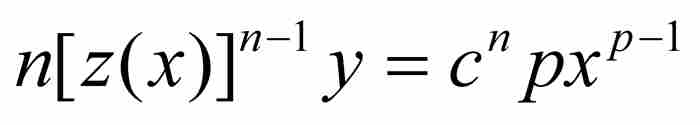 (9)
(9)
4 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 23。
现代读者的反应很可能是,“别那么快,艾萨克!”当牛顿用o作除数的时候,o无疑不等于零。但是过了一会,o就变成零了。一言以蔽之,这里埋伏了隐患。这种零与非零的对应在随后的一个多世纪一直困扰着分析学家们。本书后面将更多地讨论这个问题。
不过,牛顿的推导仍然继续进行。在式(9)中,他代换了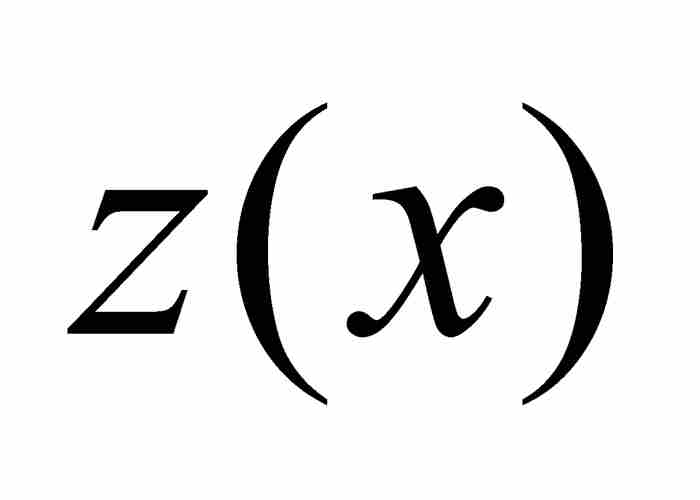 ,c和p并且解出
,c和p并且解出
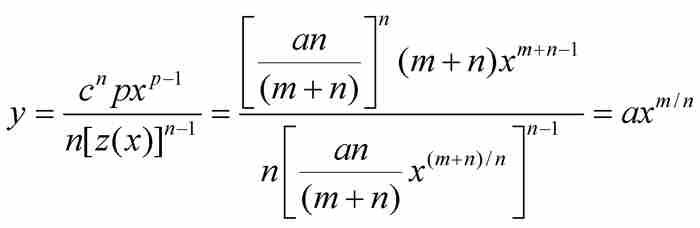
于是,牛顿从他的假设“ABD的面积为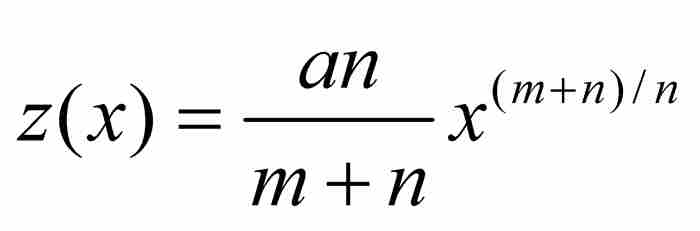 ”出发,推出曲线AD必定满足方程
”出发,推出曲线AD必定满足方程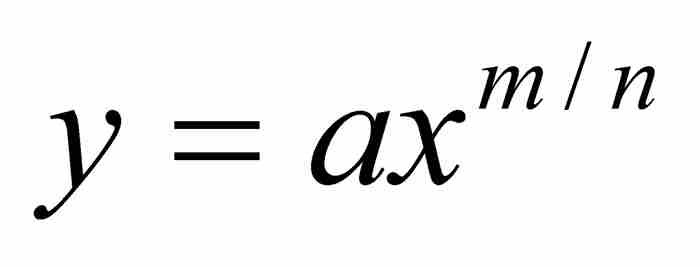 。从本质上说,他微分了积分。然后,在没有进一步证明的情况下,他指出:“与此相反,如果
。从本质上说,他微分了积分。然后,在没有进一步证明的情况下,他指出:“与此相反,如果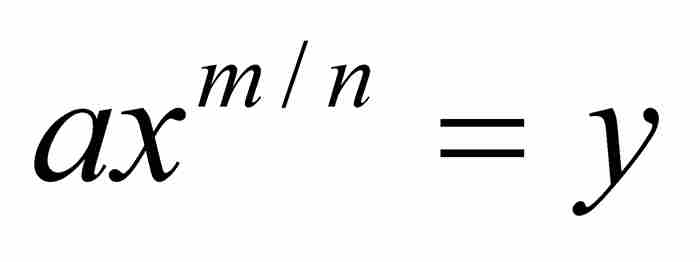 ,那么就有
,那么就有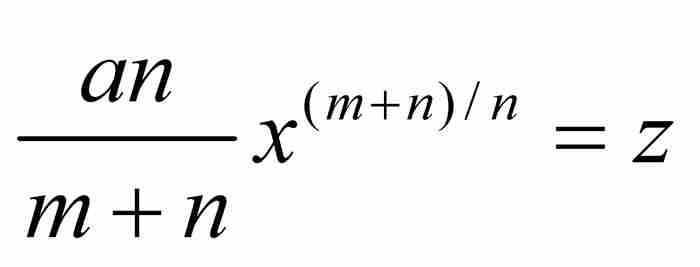 。”这就完成了他对法则1的证明。5
。”这就完成了他对法则1的证明。5
5 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 23。
这是一种特别扭曲的逻辑。从曲线之下的面积积分z导出y的方程之后,牛顿断言这种关系在相反的方向也存在,并且曲线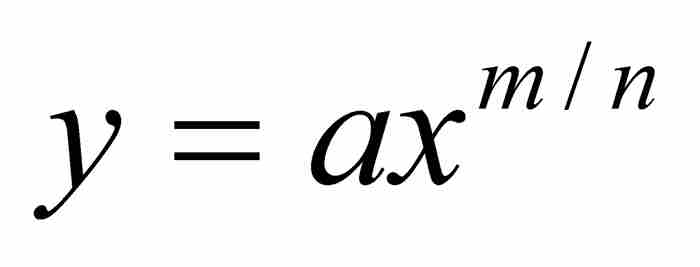 之下的面积就是
之下的面积就是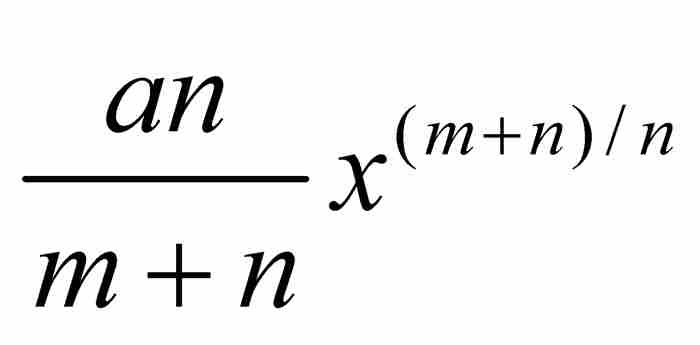 。这样的论证给我们留下杂乱无章的感觉,因为其中包含很大的逻辑漏洞。牛顿数学论文集的编辑Derek Whiteside把这个求面积的证明恰当地描写成“流数术的一种简洁的难以理解的形式”。6 另一方面,记住这个起源是很重要的。牛顿在微积分漫长的创建过程的开头就给出了法则1的证明。在他那个时代,这个证明是开山之作,并且他的结论是正确的。Richard Westfall在其评论中说,“然而概括地说,《分析学》确实展示了流数方法的整体范围和威力”,看起来这是真实的。7
。这样的论证给我们留下杂乱无章的感觉,因为其中包含很大的逻辑漏洞。牛顿数学论文集的编辑Derek Whiteside把这个求面积的证明恰当地描写成“流数术的一种简洁的难以理解的形式”。6 另一方面,记住这个起源是很重要的。牛顿在微积分漫长的创建过程的开头就给出了法则1的证明。在他那个时代,这个证明是开山之作,并且他的结论是正确的。Richard Westfall在其评论中说,“然而概括地说,《分析学》确实展示了流数方法的整体范围和威力”,看起来这是真实的。7
6 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. xiii。
7 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, p. 205。
无论如今的评判如何,牛顿当初是感到满意的。牛顿在《分析学》中没有给出证明的另外两条法则如下:
法则 2 由简单曲线构成的复杂曲线的面积:若y的值由若干项构成,那么它的面积等于其中每一项的面积之和。8
8 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 4。
法则 3 所有其他曲线的面积:如果y的值或者它的任何项比上述曲线更复杂,那么必须把它分解成更简单的项……,然后应用前面两条法则,就可以获得欲求曲线的面积。9
9 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 6。
牛顿的第二条法则断定有限项和的积分等于各项积分的和。他用了两个例子来说明这条法则。第三条法则断言,当遇到更复杂的表达式时,首先需要将其“化简”成无穷级数,再通过第一条法则对级数的每一项求积分,然后再对结果求和。
最后这条法则是一个富有吸引力的主张。更恰当地说,这是最后一个前提条件,牛顿需要用它导出数学上的一个重大结果:一个角的正弦的无穷级数。出自《分析学》的这个重要定理是这一章最有意义的主题。
牛顿的正弦级数推导
考虑图1-3中以原点为圆心和半径等于1的圆的四分之一。同以前一样,令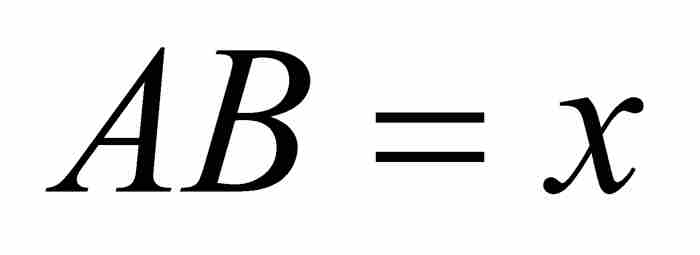 ,
,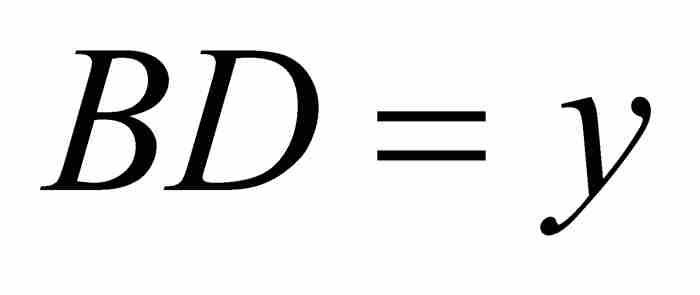 。牛顿的第一个目标是求圆弧αD的长度的表达式。1
。牛顿的第一个目标是求圆弧αD的长度的表达式。1
1 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, pp. 18-21。
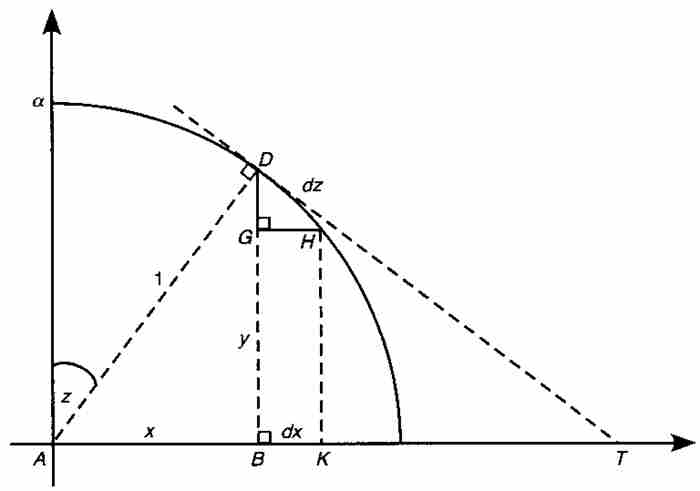
图 1-3
从D引出圆弧的切线DT,并且令BK为“基底AB的增量”。在一种表示法中,我们令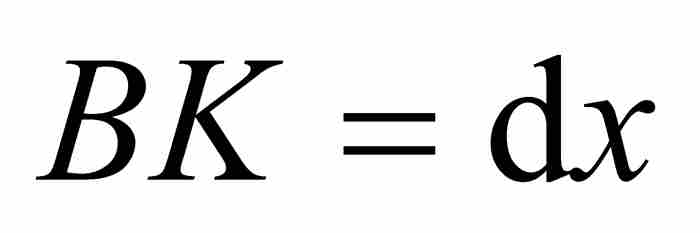 ,这成为牛顿之后的一种标准记号。这样就建立了一个“无限小的”直角三角形DGH,牛顿把它的斜边DH视为圆弧αD的增量。我们用
,这成为牛顿之后的一种标准记号。这样就建立了一个“无限小的”直角三角形DGH,牛顿把它的斜边DH视为圆弧αD的增量。我们用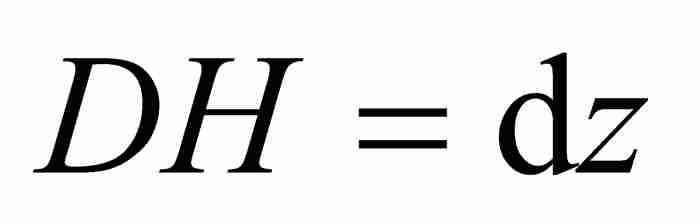 表示,其中
表示,其中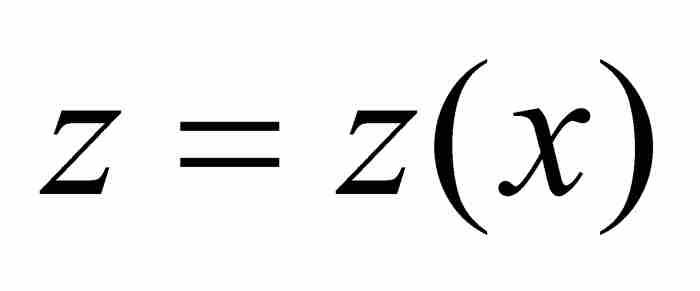 代表圆弧αD的长度。由于这一切都是发生在单位圆内,所以
代表圆弧αD的长度。由于这一切都是发生在单位圆内,所以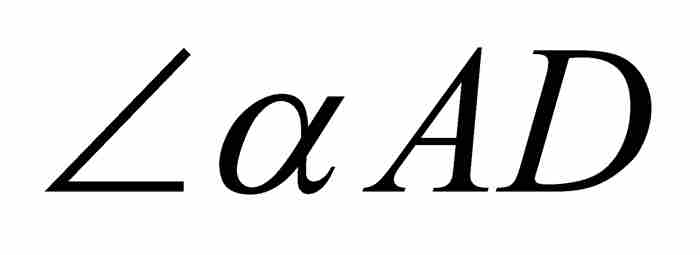 的弧度也是z。
的弧度也是z。
在这种情况下,无限小的三角形DGH与三角形DBT相似,所以有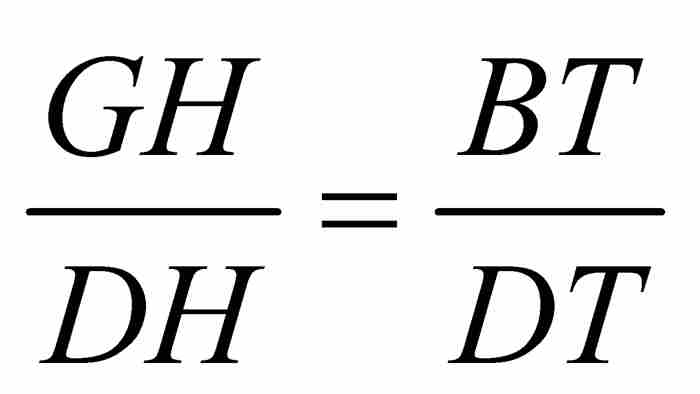 。此外,半径AD与切线DT垂直,所以高线BD将直角三角形ADT分成两个相似三角形DBT和ABD。由此推出,
。此外,半径AD与切线DT垂直,所以高线BD将直角三角形ADT分成两个相似三角形DBT和ABD。由此推出,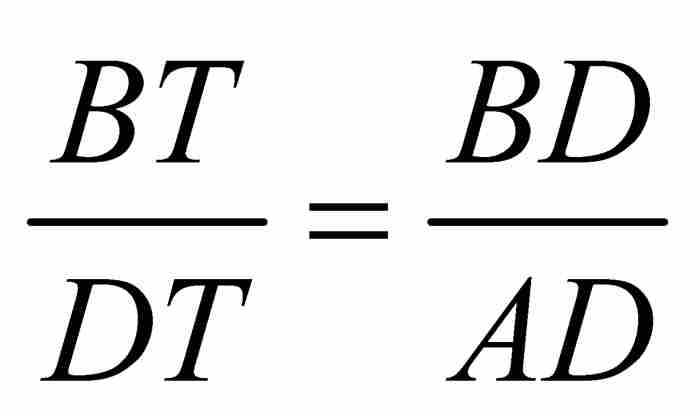 。从这两个比例关系,我们可以推出
。从这两个比例关系,我们可以推出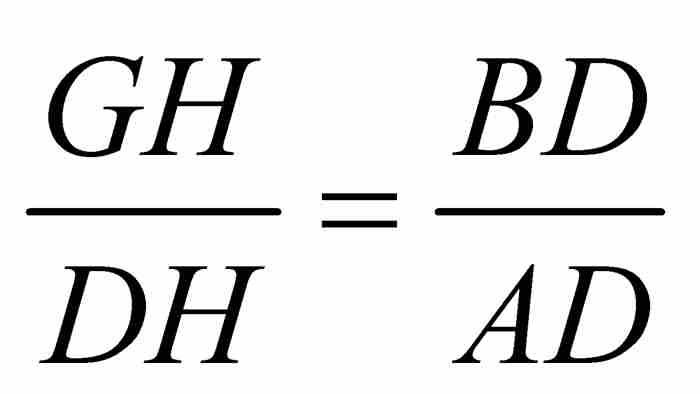 。采用上面的微分记号,可得
。采用上面的微分记号,可得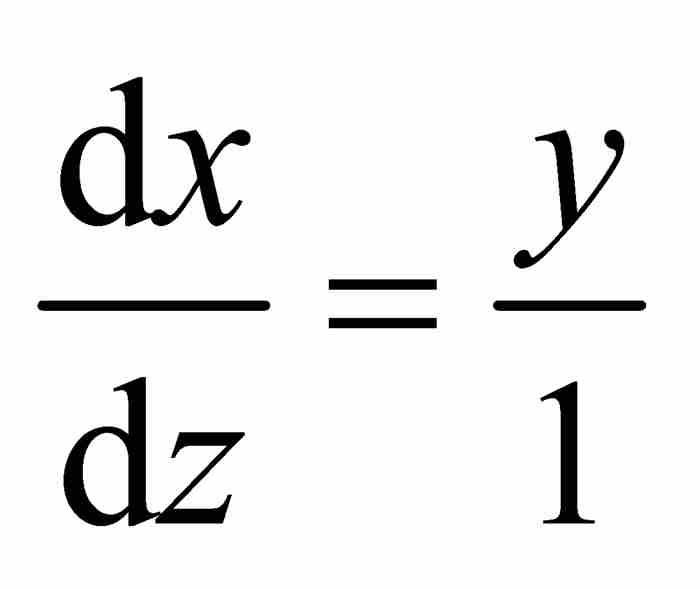 。因此,
。因此,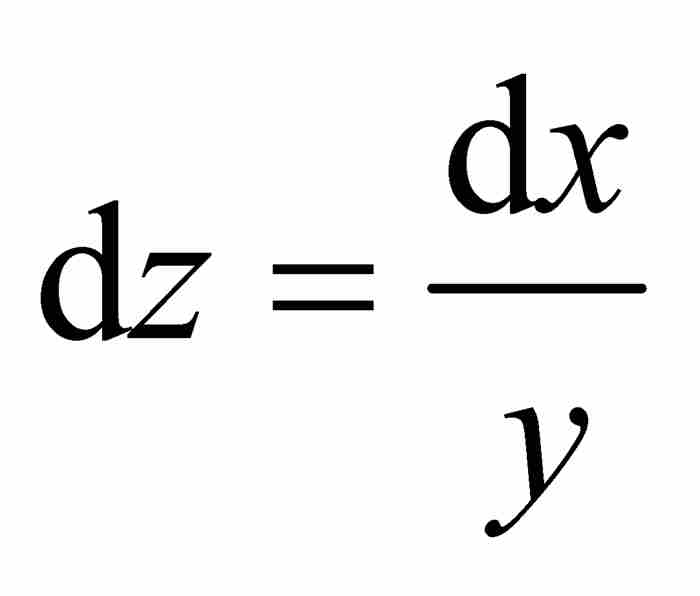 。
。
在下一步推导中牛顿利用圆的关系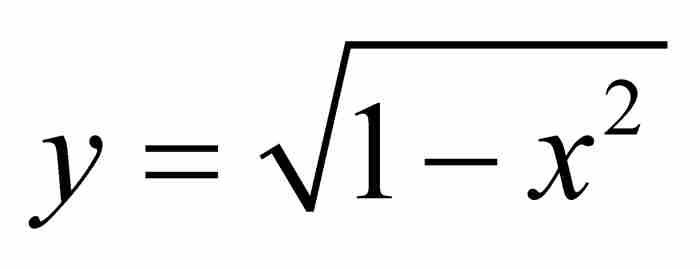 ,得到
,得到 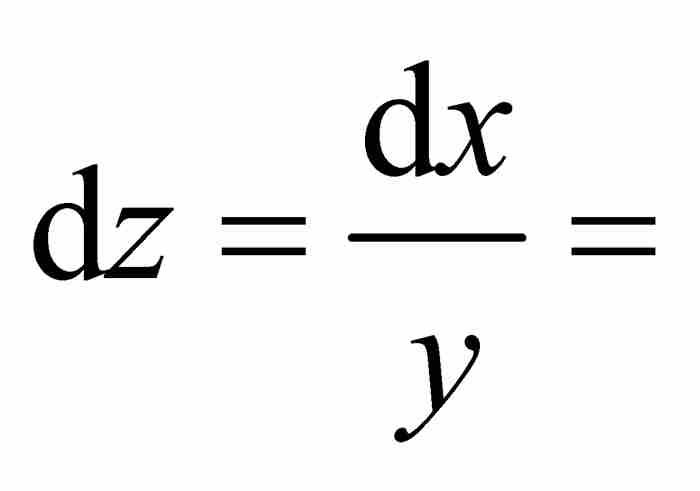
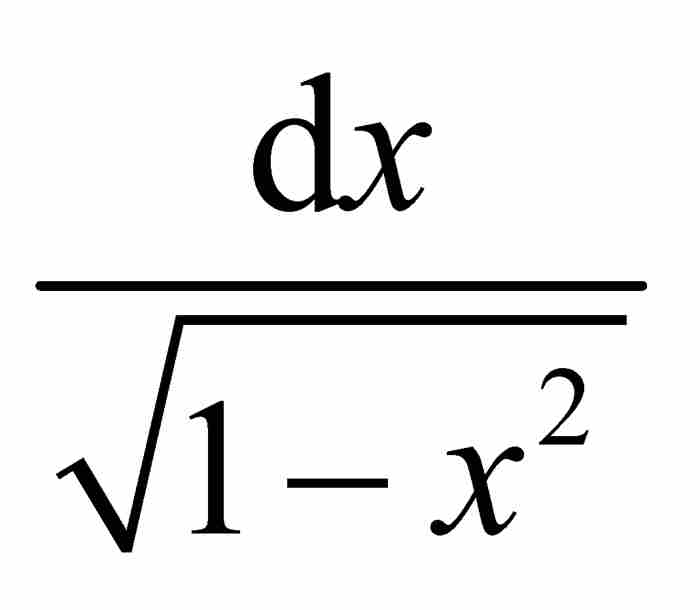 。像式(3)那样展开
。像式(3)那样展开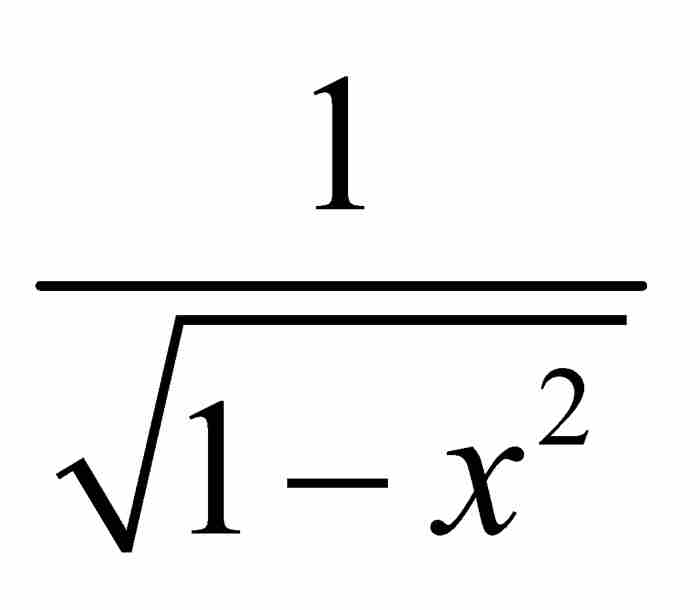 ,导出
,导出
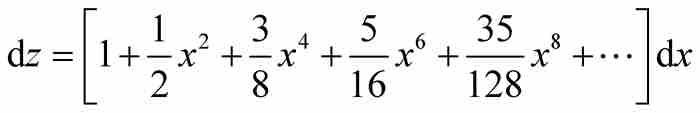
所以
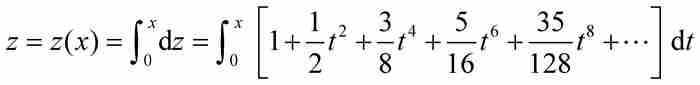
对这些单独的乘方项求面积,并用法则3对结果求和,牛顿得到圆弧αD的弧长为
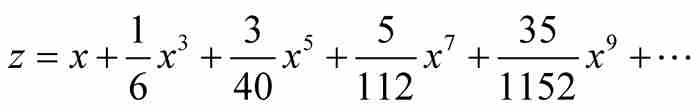 (10)
(10)
再度审视图1-3,我们看到z不仅仅是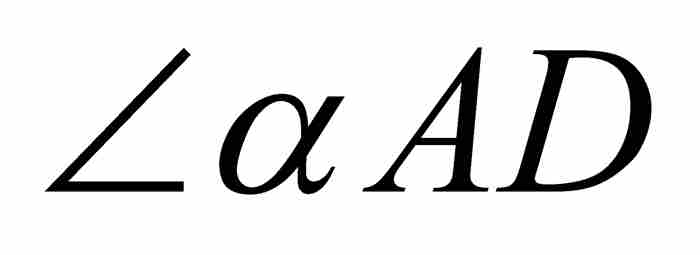 的弧度,也是
的弧度,也是 的弧度。由三角形ABD可知,
的弧度。由三角形ABD可知,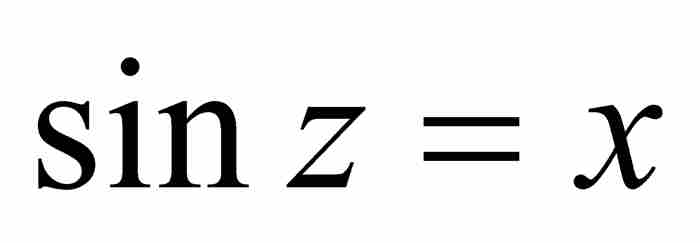 ,所以
,所以

因此,从代数表达式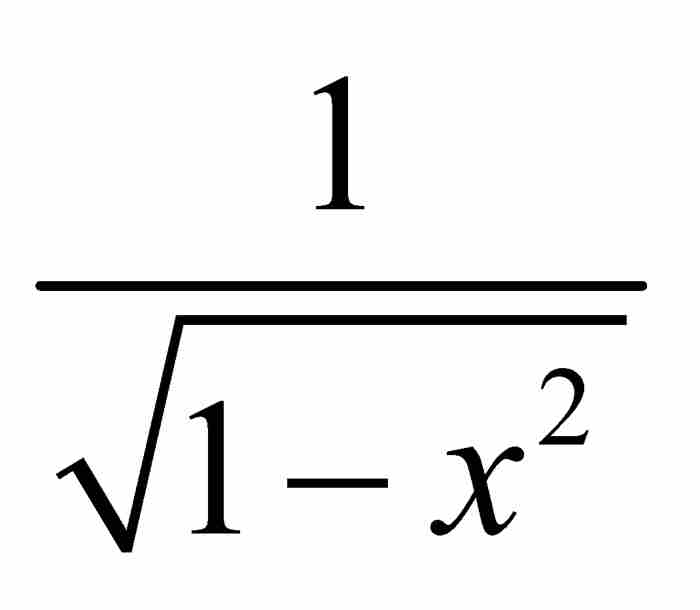 开始,牛顿利用他的广义二项展开式和基本的积分推导出反正弦的级数,这是本质上更为复杂的一个关系式。
开始,牛顿利用他的广义二项展开式和基本的积分推导出反正弦的级数,这是本质上更为复杂的一个关系式。
然而,牛顿还有一个锦囊妙计。他不去求用横坐标(x)表示的弧长(z)的级数,而是寻找相反的过程。他写道:“如果需要从已知弧长αD求AB的正弦,那么我对上面导出的表达式求根。” 2 就是说,牛顿利用他的逆过程,将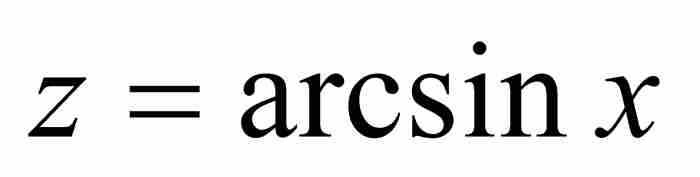 的级数转换成
的级数转换成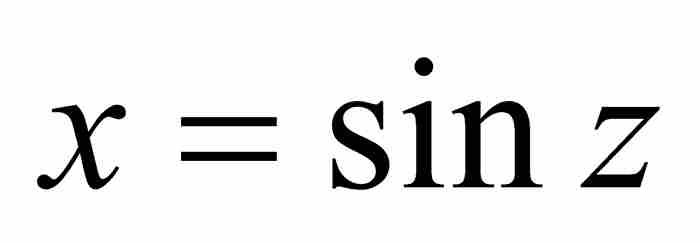 的级数。
的级数。
2 Derek Whiteside(ed.), The Mathematical Works of Isaac Newton, vol.1, Johnson Reprint Corp, 1964, p. 20。
按照前面描述的方法,我们从把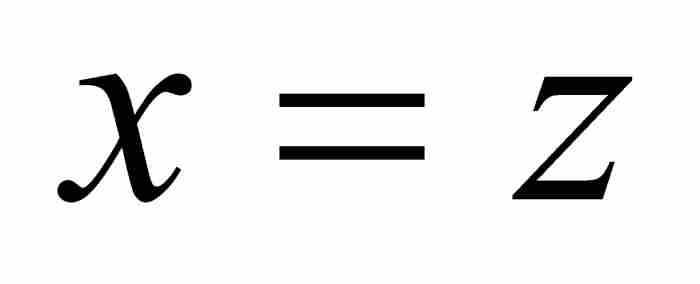 作为第一项开始。为把级数展开推进到下一步,将
作为第一项开始。为把级数展开推进到下一步,将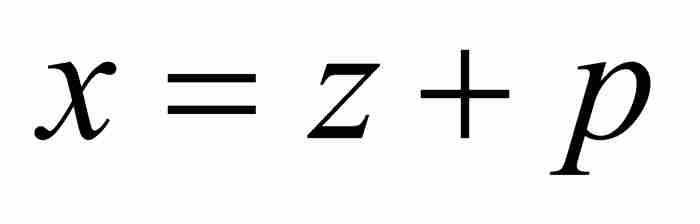 代入式(10),并且解出
代入式(10),并且解出
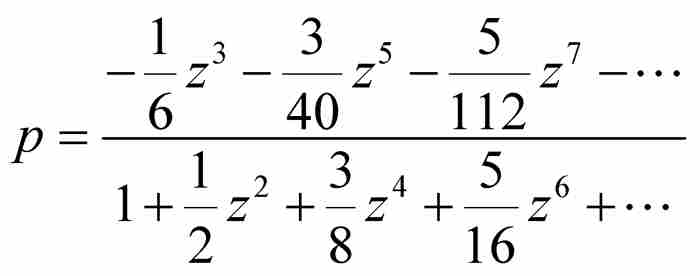
我们仅从这个解中保留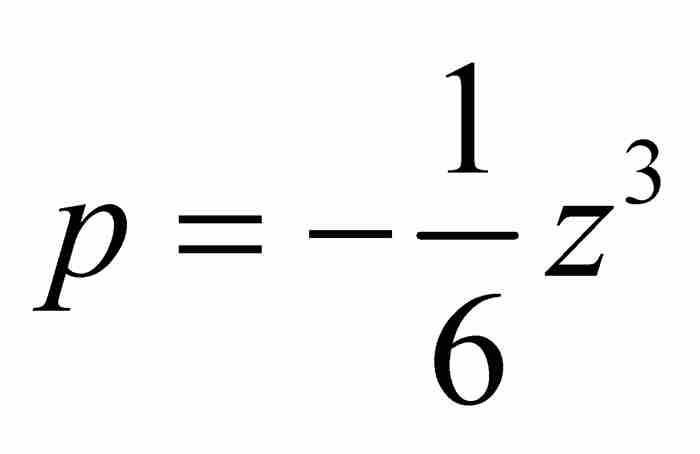 。这样就将级数扩展成
。这样就将级数扩展成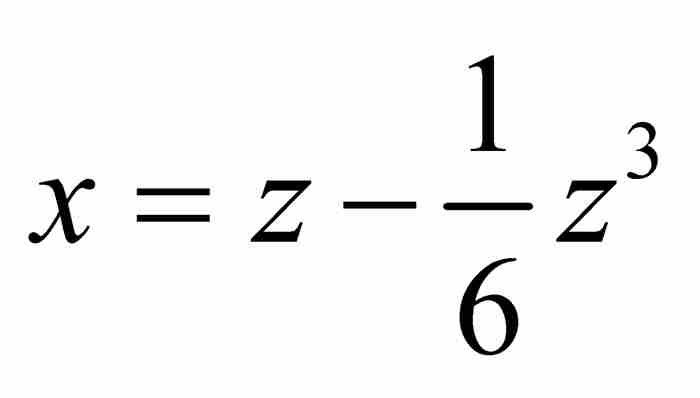 。下一步引进
。下一步引进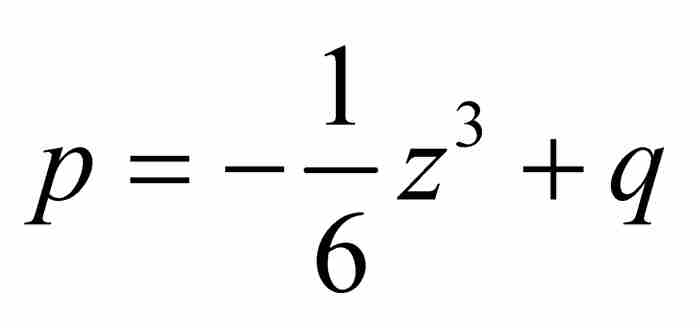 ,继续这个逆过程,解出
,继续这个逆过程,解出
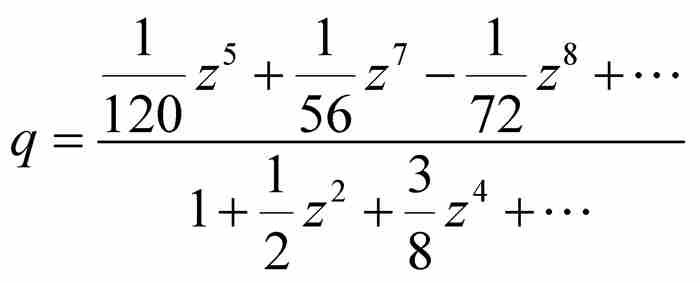
或者化简为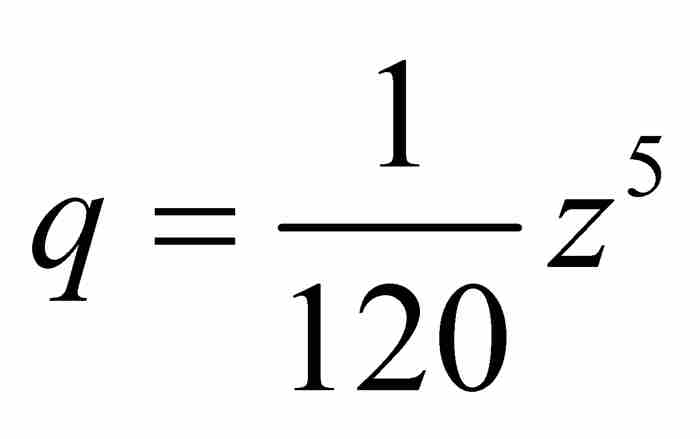 。到这一步,级数变成
。到这一步,级数变成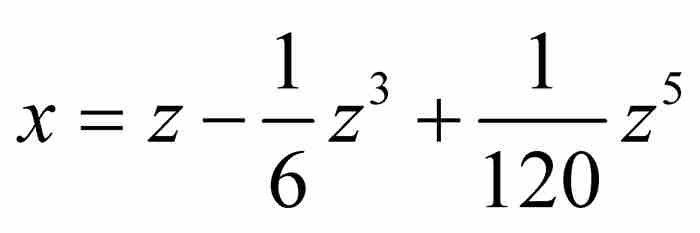 ,并且,也许像牛顿所说的那样,我们“继续随意地”推导下去,直至发现级数项的通用模式,然后书写下分析学中最重要的一个级数:
,并且,也许像牛顿所说的那样,我们“继续随意地”推导下去,直至发现级数项的通用模式,然后书写下分析学中最重要的一个级数:
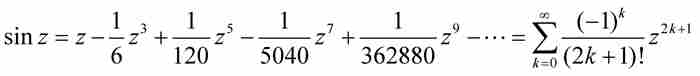
为了获得更准确的曲线弧长,牛顿又推导了余弦级数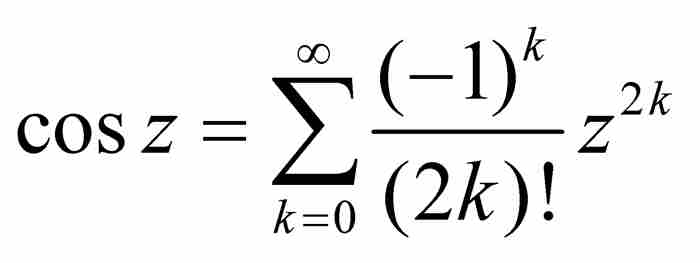 。按照Derek Whiteside的说法,“关于正弦和余弦的这些级数第一次出现在欧洲人的手稿中”。3
。按照Derek Whiteside的说法,“关于正弦和余弦的这些级数第一次出现在欧洲人的手稿中”。3
3 Derek Whiteside (ed.), Mathematical Papers of Isaac Newton, vol. 2,Cambridge University Press, 1968, p. 237。

牛顿的正弦级数和余弦级数(1669)
对我们来说,这种推导所兜的圈子看起来是不可思议的。我们现在把正弦级数视为不过是泰勒公式和微分学的一个微不足道的推论而已。所以我们自然而然地以为它一直就是这样简单的。但是,正如我们所见,牛顿克服了重重困难才得到这个结果。他运用了积分法则而不是微分法则;他从(我们认为)偶然的反正弦级数产生正弦级数;同时,他需要运用他所提出的复杂的逆过程方案来完成全部推导。
这个历史片段提醒我们,数学并不是按照现在教科书中的方式发展的。相反,它是通过断断续续地在出乎意料的惊喜中发展起来的。事实上,那是相当有趣的,因为历史在一下子变得有意义、美好和出乎意料的时候,它是极具吸引力的。
谈到出乎意料这个话题,我们就Derek Whiteside在上面那段话中的评判补充一句。看起来牛顿并不是第一个发现正弦级数的人。印度数学家尼拉坎塔(1445—1545)在公元1545年描述过这个级数,并且把它归功于更久远的前辈马达维(生活在公元1400年前后)。关于这些发现和印度数学中的优良传统的叙述可以从文献4和5中查到。但是,这些成果在牛顿活跃的时代的欧洲自然不为人们所知。
4 David Bressoud, “Was Calculus Invented in India?” The College Mathematics Journal, vol. 33 (2002), pp. 2-13。
5 Victor Katz, A History of Mathematics:An Infroduction, Harper-Collins, 1993, pp. 451-453。
我们以两点评论作为本章的结束语。第一,牛顿的《分析学》是一本真正的数学经典,是任何一位对微积分的历程感兴趣的人都应拥有的读物。从中可以瞥见这位历史上最具创造力的思想家在其才智发展的早期阶段的情况。
第二,用现在的眼光看来,一场轰轰烈烈的革命开始了。年轻的牛顿以其超越时代的专业才能和洞察力把无穷级数和流数法结合起来,将数学的前沿推向若干新的发展方向。与他同时代的詹姆斯·格雷戈里(1638—1675)评论过去的初等方法对于产生同样关联的这些新方法,就如同“黎明的晨曦对于正午的阳光”。6 正如我们在后面几章将要多次看到的,格雷戈里这种令人陶醉的描述是恰如其分的。同时,第一个走向这条激动人心的道路的人是牛顿,他确实不愧为“一位具有非凡天赋和卓越才能的人物”。
6 C. Gerhardt (ed.), Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern, vol. 1, Mayer & Müller Berlin, 1899, p. 170。