第9章 魏尔斯特拉斯
04-13Ctrl+D 收藏本站

卡尔·魏尔斯特拉斯(1815—1897)
正如我们所知,在19世纪,数学家们将微积分的严格性提高到一个新的水平。然而,按照我们今天的标准,这些成就并不是无可挑剔的。当你拜读那个时期的数学文献时,犹如聆听音乐大师肖邦在一架三两琴键失调的钢琴上演奏乐章,固然能够怡然自得地鉴赏音乐的神韵,不过间或也会听到些许畸变之音。只有在微积分中消除不精确性的最后痕迹,分析论证变成对于一切实用目的都是无可置疑的时候,数学的新纪元才能到来。魏尔斯特拉斯是实现这个最后转变的最大功臣。
魏尔斯特拉斯沿着一条非传统的道路崭露头角。他在学生时代,成绩并不优异,却热衷于狂饮啤酒和击剑。到30岁时,魏尔斯特拉斯成为德国一所偏僻的大学预科学校(高级中学)的教师,这所学校远离欧洲的学术中心。在白天,他对学生讲授算术和书法,只有在课余且批改完学生的作业之后,年轻的魏尔斯特拉斯方能致力于他的数学研究。1
1 这段传略摘自Dictionary of Scientific Biography, vol. XIV, C. C. Gillispie, editor-in-chief, Scribner, 1976, pp. 219-224。
这位名不见经传的来自德国一个不知名小镇的中学教师,在1854年发表了一篇关于阿贝尔积分的论文。凡是读过这篇文章的数学家,无不惊讶万分。很明显,这篇论文的作者,必定是具有非凡天赋的奇才。不出两年,魏尔斯特拉斯在柏林大学谋求到一个职位,受聘为这所大学的教授,并跻身于世界杰出数学家的行列。他的事迹,算得上是一个真实灰姑娘的故事。
魏尔斯特拉斯对分析学作出的贡献是极为显著的,正如他的教学方法是举世闻名的一样。随着他的赫赫名声在德国和欧洲的传播,这位数学大师吸引着渴望师从他的年轻数学家们。在他的门下云集了一大批追随者。那时人们可以见到这样一种真实的场景,患有严重眩晕症的魏尔斯特拉斯坐在一把安乐椅上授课,而由一名指派的学生把他的话写在黑板上。(这样一种讲课方式令后来的教授们羡慕不已,然而是几乎无法重现的。)
如果说魏尔斯特拉斯的执教风格是异乎寻常的话,那么他对待发表研究成果的态度也是与众不同的。尽管他的讲课充满了新颖的观点和重要概念,但是他疏于发表文章,而是经常让别人从他们自己的著述中去传播这样的知识。因此人们发现,他的成果是笼统地属于魏尔斯特拉斯学派的。那些信仰“不发表就是毁灭”的现代学者们,很难理解这种非占有式的学术观念。魏尔斯特拉斯以创立具有重大意义的数学为己任,宁愿去冒毁灭的风险。
魏尔斯特拉斯学派通过魏尔斯特拉斯本人或者他的门生们发表的研究成果,对分析学赋予逻辑上的一种无与伦比的精确性。他矫正了许多难以捉摸的错误概念,证明了大量重要的定理,并且构造出一个令数学家们惊叹不已的处处连续而又不可微的函数的反例。在这一章,我们会了解到卡尔·魏尔斯特拉斯为什么被誉为“现代分析学之父”。2
2 Eric Temple Bell, Men of Mathematics, Simon & Schuster, 1937, p. 406。
回到基本问题
不妨回忆一下,柯西是怎样在极限的基础上建立他的微积分的。在他给出的定义中有这样一句话:
当属于一个变量的相继值无限地趋近某个固定值时,如果以这样一种方式告终,变量值同固定值之差小到我们希望的任意小,那么这个固定值就称为其他所有值的极限。
对于我们而言,这句话的某些方面,例如 “趋近”这个行动,似乎不是一种令人满意的表达方式。趋近是指某种实际的动作吗?如果是这样,那么在谈论极限之前我们必须考虑时间和空间的概念吗?此外,这个过程“告终”的含义是什么?总之,所有这一切尚需作最后修订。
魏尔斯特拉斯重新给出极限的定义:
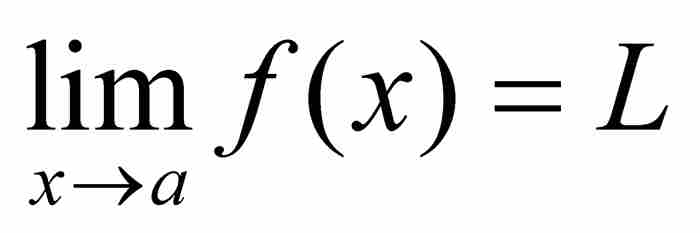 ,当且仅当对于任意ε > 0,存在一个δ > 0,
,当且仅当对于任意ε > 0,存在一个δ > 0,
使得只要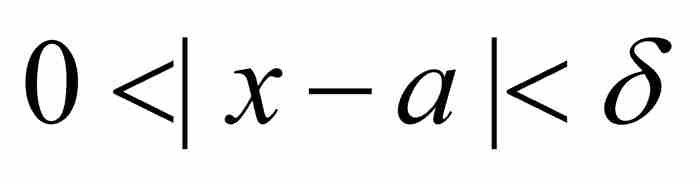 ,就有
,就有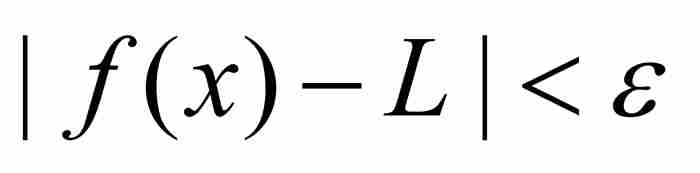 (1)
(1)
这个完美的定义同柯西对极限所说的话形成鲜明对比。在这里,没有任何动作,而且不涉及时间。这是一个静态的而非动态的定义,同时又是一个代数的而非几何的定义。定义的核心是一个关于不等式的断言。并且,可以把这个定义作为证明各种极限定理的基础,例如,用它给出“和的极限等于极限的和”的确切证明。至此,对于这样的定理可以进行像欧几里得命题那样完全严格的证明。
有人可能提出这样的观点:需要为精确性付出某种代价,因为魏尔斯特拉斯提出的严格定义缺乏直觉的魅力和几何上的直观性。毫无疑问,还需要慢慢适应像式(1)这样的陈述。除此之外,几何直观是值得怀疑的,而魏尔斯特拉斯给出的这个纯粹的分析定义丝毫不牵涉空间与时间。
魏尔斯特拉斯除了重新阐明各种关键性概念外,还领会到了这些概念的含义,这是他的前辈们未能做到的。一个例子就是一致连续性,柯西同这种函数性质失之交臂。我们回忆一下,柯西在逐点的基础上定义了连续性,他指出,如果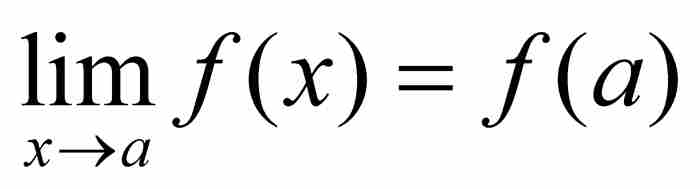 ,那么f在a是连续的。采用魏尔斯特拉斯的语言,这意味着对于每个ε > 0,存在一个对应的δ > 0,使得只要
,那么f在a是连续的。采用魏尔斯特拉斯的语言,这意味着对于每个ε > 0,存在一个对应的δ > 0,使得只要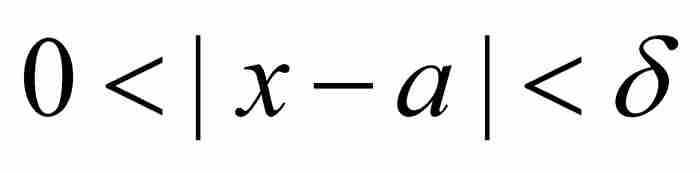 ,就有
,就有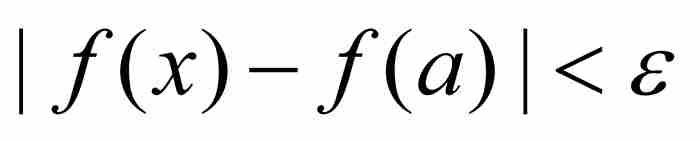 。因此,对于一个固定的“靶子”ε 和一个已知的a,我们能够求出所需的δ。但是此处的δ 同时依赖ε 和a。当考虑一个不同的a值时,我们如果保持同一个ε,一般而言,必须调整对δ 的选择。
。因此,对于一个固定的“靶子”ε 和一个已知的a,我们能够求出所需的δ。但是此处的δ 同时依赖ε 和a。当考虑一个不同的a值时,我们如果保持同一个ε,一般而言,必须调整对δ 的选择。
爱德华·海涅(1821—1881)在出版物中首次作出这种区分,不过他暗示“这个普遍概念”是他的良师益友魏尔斯特拉斯传授给他的。1海涅给出了一致连续的定义:如果对于每个ε > 0,存在一个δ > 0,使得函数f的定义域内的任意两点x和y,只要它们的距离小于δ,就有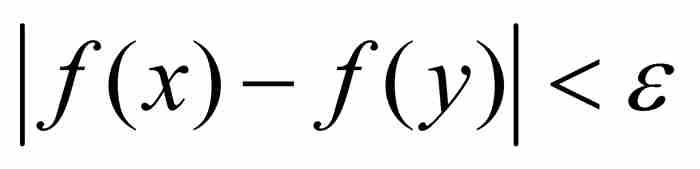 ,那么 f 在其定义域上是一致连续的。在本质上,这意味着“一个δ适用于所有ε”,所以在这个一致距离之内的点,它们之间的函数值之差将在ε的范围内。
,那么 f 在其定义域上是一致连续的。在本质上,这意味着“一个δ适用于所有ε”,所以在这个一致距离之内的点,它们之间的函数值之差将在ε的范围内。
1 E. Hairer and G. Wanner, Analysis by Its History, Springer- Verlag, 1996, p. 215。
显然,一个一致连续的函数,在每个单独的点是连续的。但是,相反的结论并不成立,典型的反例是定义在开区间(0, 1)上的函数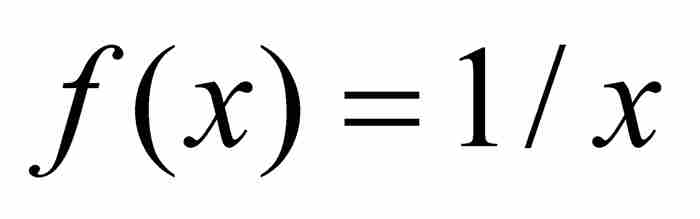 ,如图9-1所示。这个函数在(0, 1)内的每个点无疑是连续的,但是它不符合海涅的一致连续判别准则。我们考察一下何以如此。令ε = 1,我们断定不会存在一个δ > 0,使得当从(0, 1)选择满足
,如图9-1所示。这个函数在(0, 1)内的每个点无疑是连续的,但是它不符合海涅的一致连续判别准则。我们考察一下何以如此。令ε = 1,我们断定不会存在一个δ > 0,使得当从(0, 1)选择满足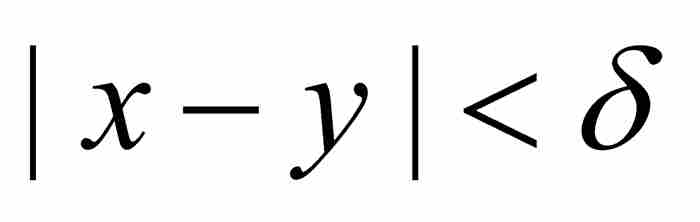 的x和y时,有
的x和y时,有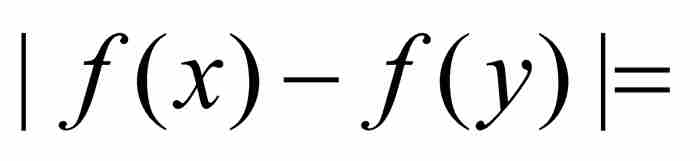
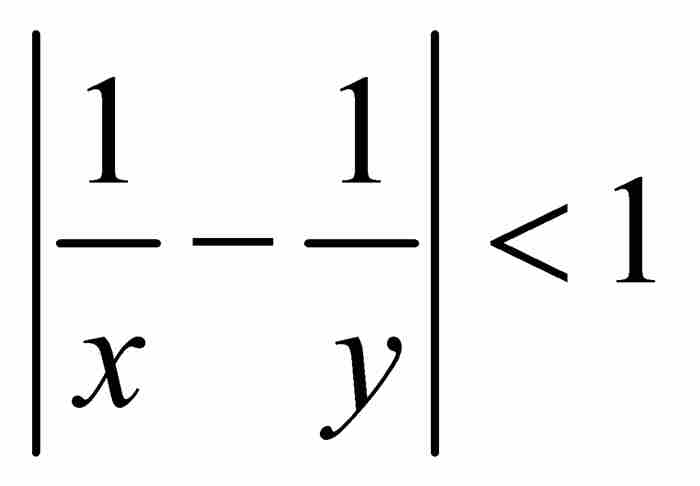 。这是因为,对于给定的δ,我们可以选择一个整数
。这是因为,对于给定的δ,我们可以选择一个整数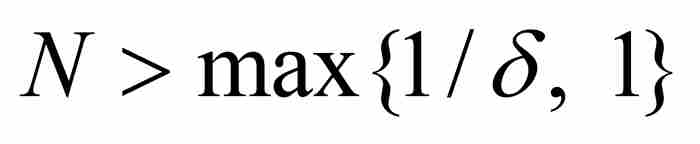 ,并且令
,并且令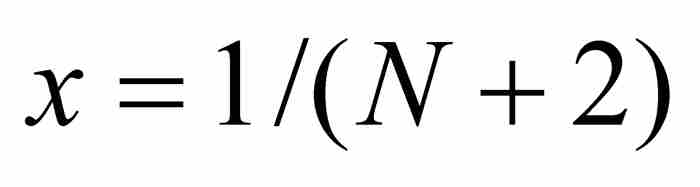 和
和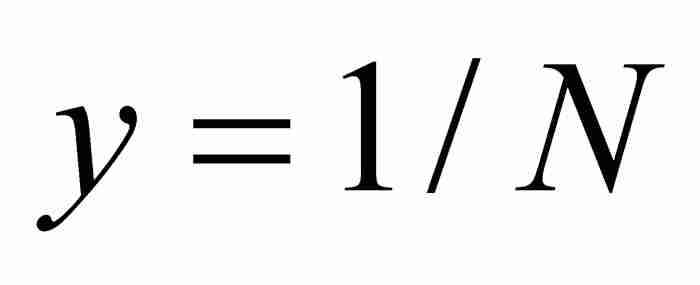 。在这种情形下,x和y同属于区间(0, 1),并且有
。在这种情形下,x和y同属于区间(0, 1),并且有
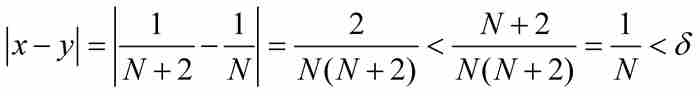
然而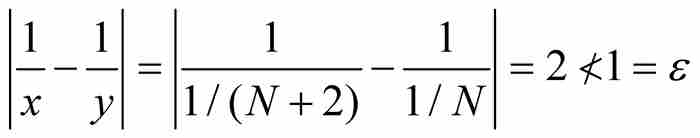 。一致连续的条件不满足。
。一致连续的条件不满足。
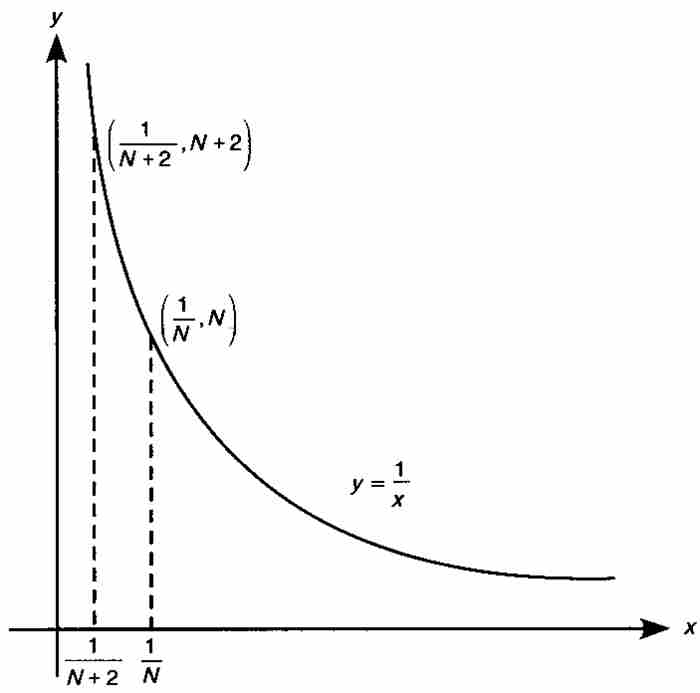
图 9-1
回顾第6章,不禁使我们想起柯西曾经论述过连续函数,同时,在他的某些证明中实际上使用了一致连续性。值得庆幸的是,当海涅在1872年证明了一个有界闭区间[a, b]上的连续函数必定是一致连续函数时,一场逻辑推理上的灾难得以避免。就是说,如果我们把函数限制在闭区间[a, b]上,那么连续性同一致连续性之间的差异将随之消失。(请注意,在上面举出的反例中,函数是定义在一个开区间上的。)所以,对于有界闭区间上的函数,当在证明中出现柯西的错误概念时,多亏海涅的结果,这使他的证明是“可补救的”。
魏尔斯特拉斯认识到一种更为重要的区分,那就是点态收敛同一致收敛之间的差异。为了考察这两种收敛概念,我们有必要暂且离开一下正题。
假定我们有一个函数序列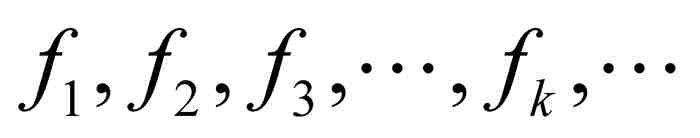 ,它们具有相同的定义域。如果在这个定义域中固定一点x,并且把它代入每个函数,遂产生一个数列
,它们具有相同的定义域。如果在这个定义域中固定一点x,并且把它代入每个函数,遂产生一个数列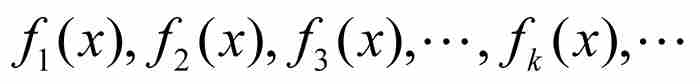 。假定对于每个单独的x,这个数列收敛。在这种情况下,在每个点x建立了由
。假定对于每个单独的x,这个数列收敛。在这种情况下,在每个点x建立了由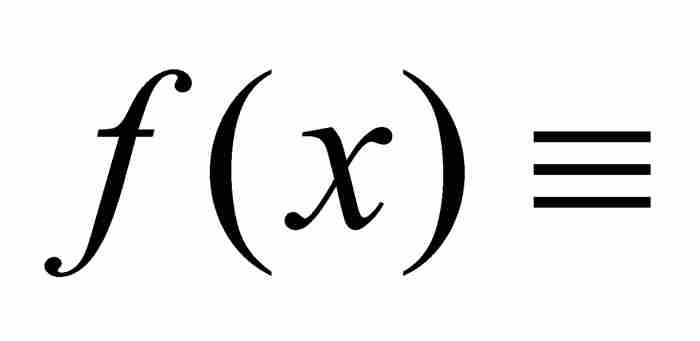
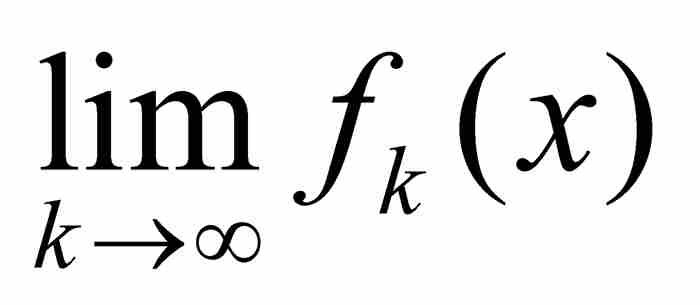 定义的新函数。我们把
定义的新函数。我们把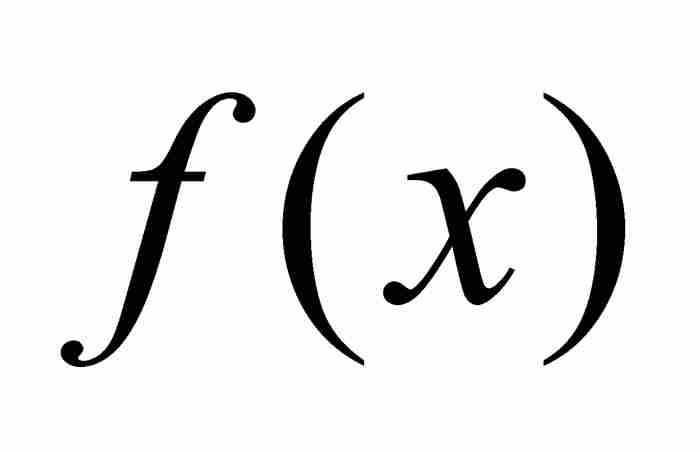 称为
称为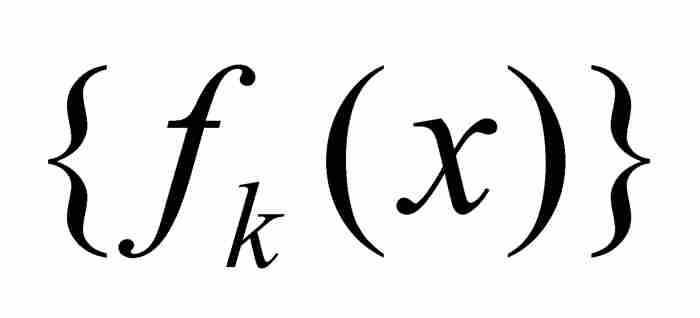 的“点态极限”。
的“点态极限”。
例如,考虑在区间[0, π]上定义的函数序列:
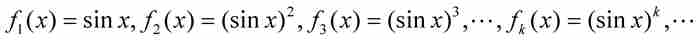
这个序列的前三个函数的图形在图9-2中画出。
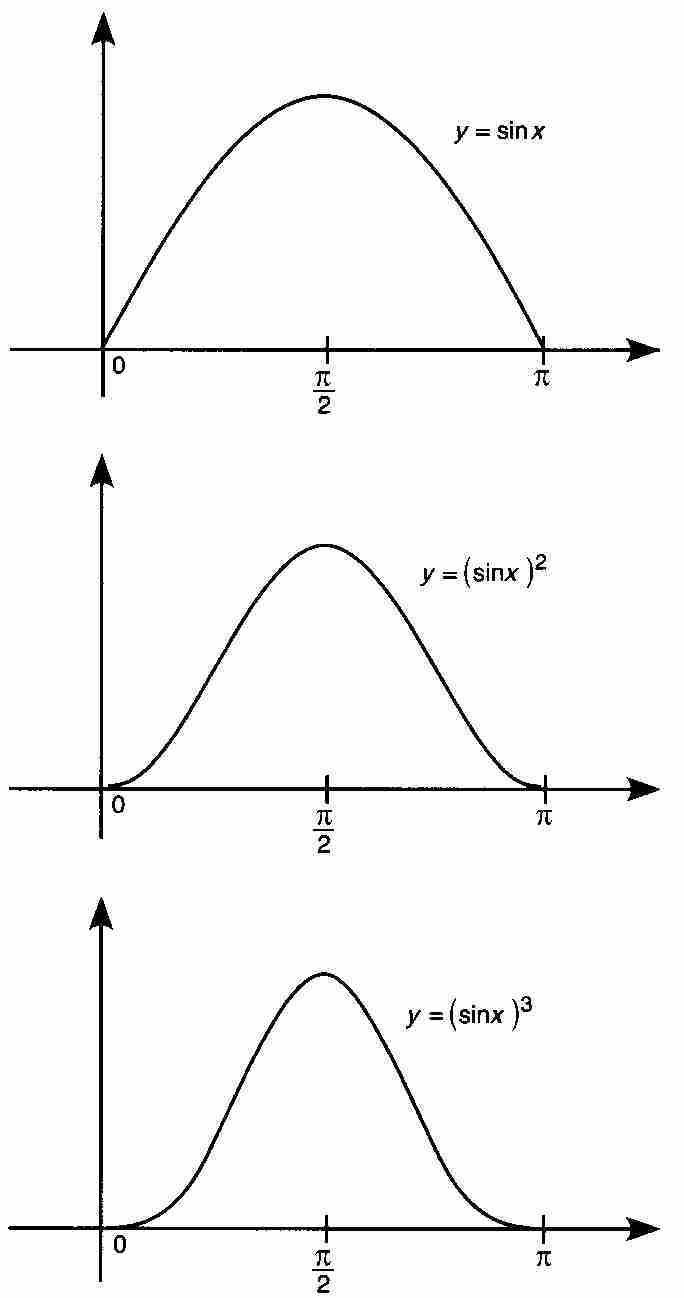
图 9-2
我们看出,对于所有k≥1,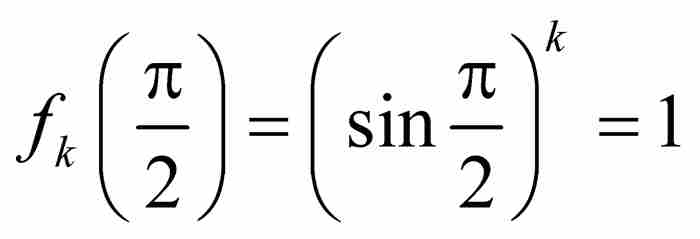 ,所以
,所以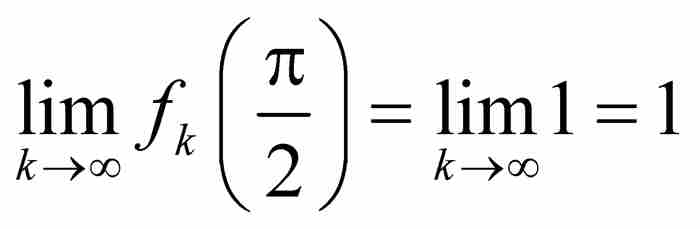 。另一方面,如果x在区间[0, π]内,但是
。另一方面,如果x在区间[0, π]内,但是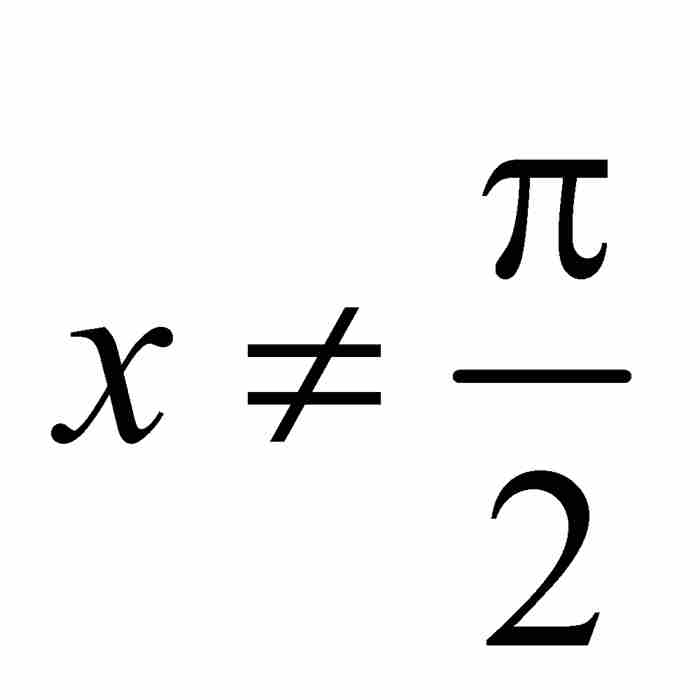 ,那么
,那么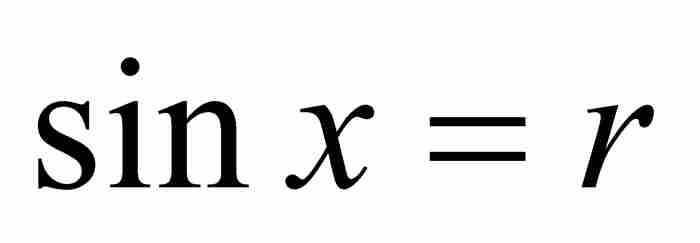 ,其中
,其中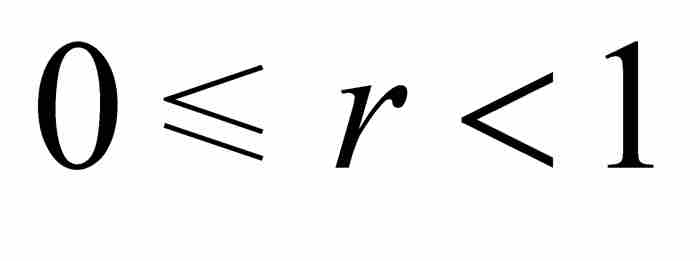 ,所以
,所以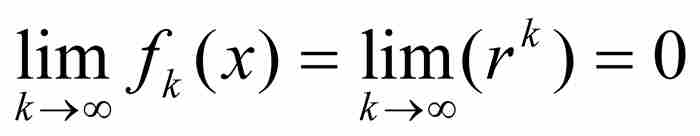 。因此,这个点态极限为
。因此,这个点态极限为
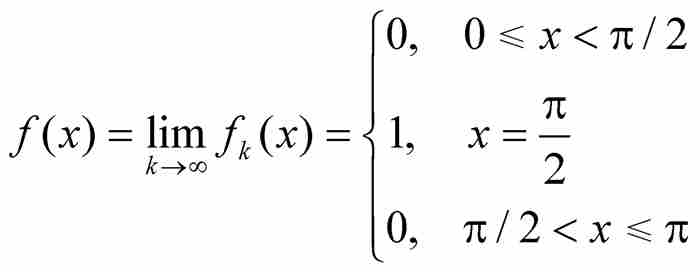
它的图形显示在图9-3中。
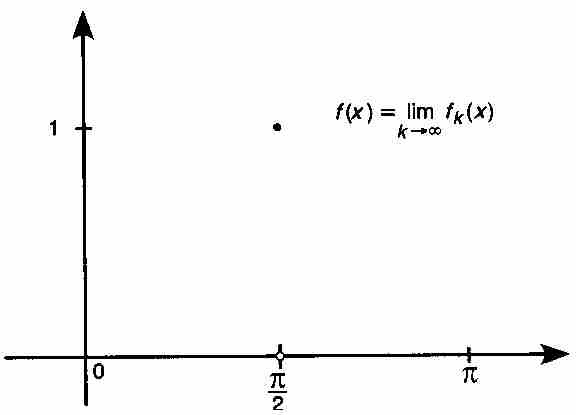
图 9-3
这个例子引出分析学中的一个重大问题:如果函数序列{fk}中的每个函数具有某种确定的性质,而f是这个函数序列的点态极限,那么f本身必须具备这种性质吗?用数学语言表述,就是问函数的一种特性是否由点态极限继承。如果每个fk是连续函数,f必定是连续函数吗?如果每个fk是可积的,f必定是可积的吗?
要是单凭直觉,可能回答“是的,为什么不是呢!”可惜,世间的事物并非如此简单。例如,连续性就不是点态极限函数继承的特性,这正是使过去的柯西和其他数学家迷惑不解的根源。2 我们只需考察一下上面的例子就会明白,函数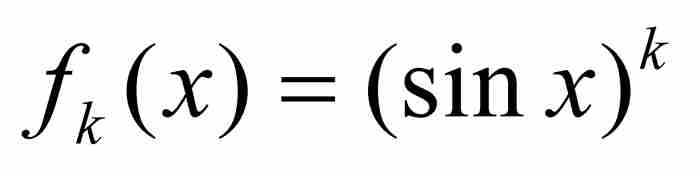 是处处连续的,然而它们在图9-3中的点态极限
是处处连续的,然而它们在图9-3中的点态极限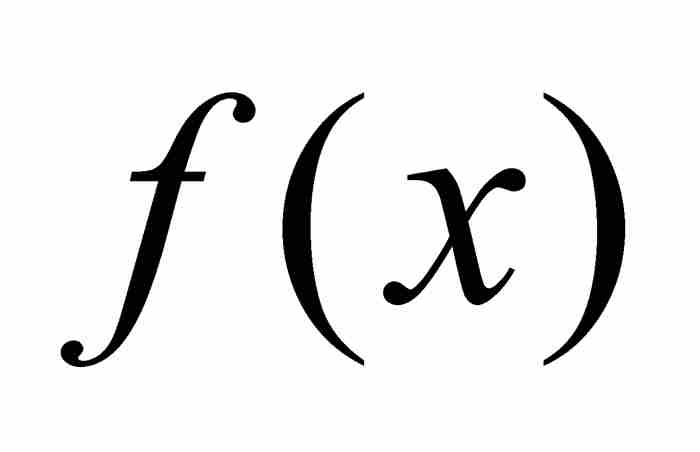 在
在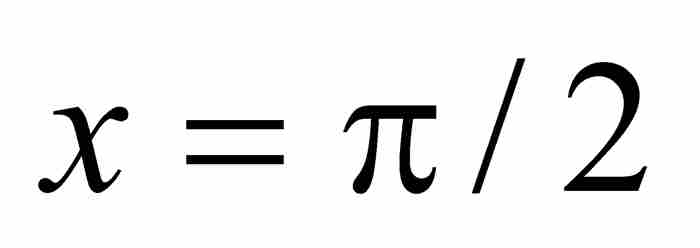 就是不连续的。这个例子同样说明,可微性也不是点态极限继承的特性。
就是不连续的。这个例子同样说明,可微性也不是点态极限继承的特性。
2 Augustin-Louis Cauchy, Oeuvres, ser. 2, vol. 3, p. 120。
关于积分又如何呢?在本书中我们已经多次见过,数学家们一度认为
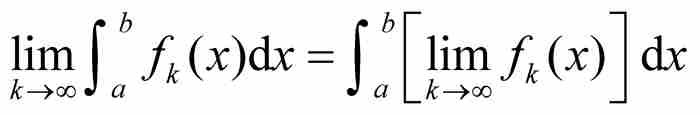
从这个等式断定,我们可以万无一失地交换两种重要的微积分运算:先积分然后取极限,或者先取极限然后积分。
为了看出这同样是错误的,我们在区间[0, 1]上定义一个由函数
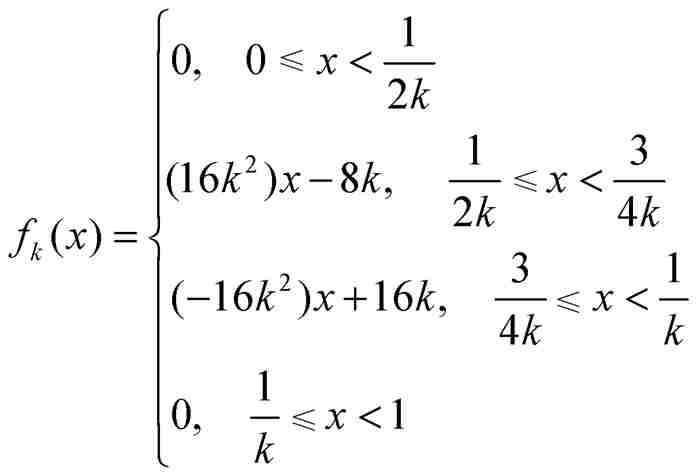
表示的序列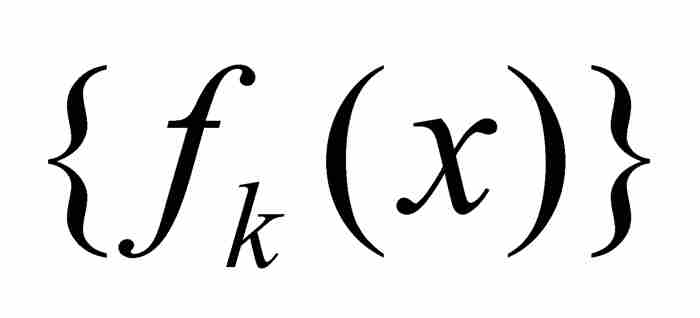 。这个函数表达式尽管看起来也许令人生畏,不过图9-4中的f1,f2和f3的图形显示,这些函数是非常平常的。每个fk(x) 都是连续函数,它们的“尖峰”在越来越靠近原点的区域上变得越来越高,但宽度越来越小。
。这个函数表达式尽管看起来也许令人生畏,不过图9-4中的f1,f2和f3的图形显示,这些函数是非常平常的。每个fk(x) 都是连续函数,它们的“尖峰”在越来越靠近原点的区域上变得越来越高,但宽度越来越小。
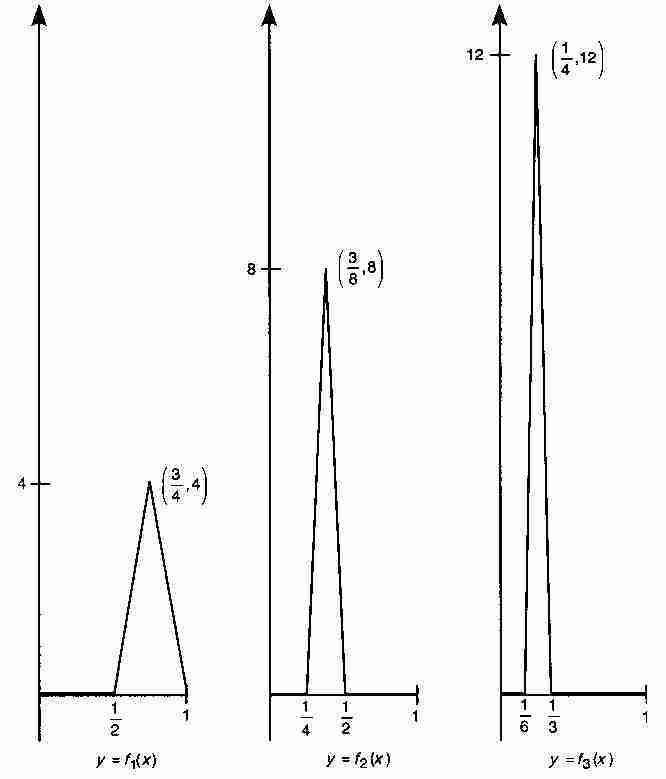
图 9-4
由于fk是连续函数,对它们可以求积分,而它们的积分作为图9-5中的三角形的面积是很容易计算的:
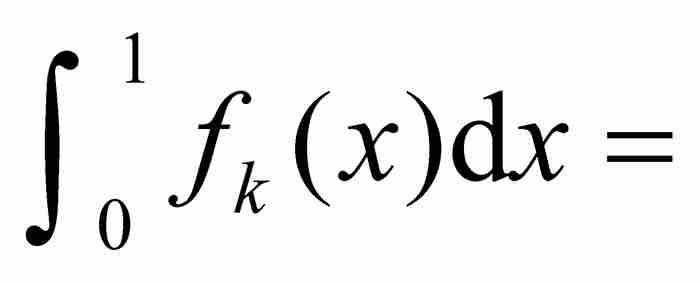 三角形面积
三角形面积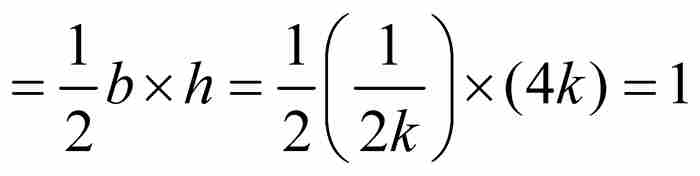
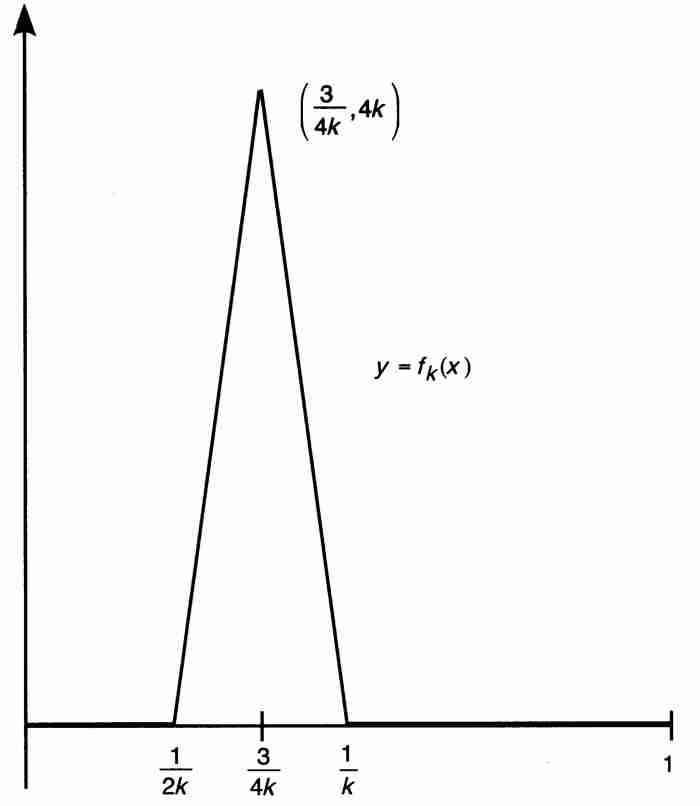
图 9-5
所以,当这些三角形区域的底边变得越来越小时,它们的高以三角形的面积保持不变这样一种方式增加。于是,显然有
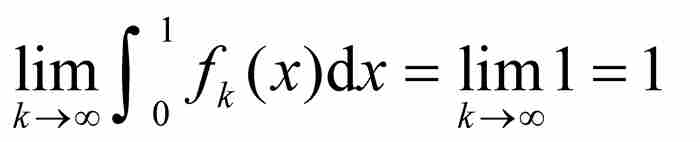 (2)
(2)
另一方面,我们断言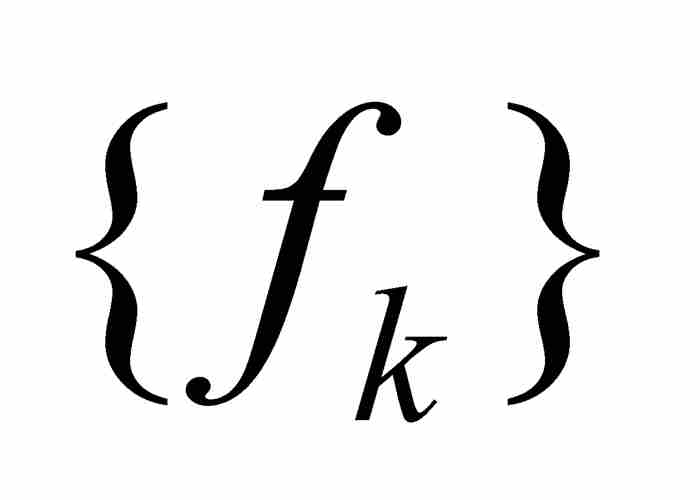 的点态极限在区间[0, 1]上处处为零。毫无疑问,
的点态极限在区间[0, 1]上处处为零。毫无疑问,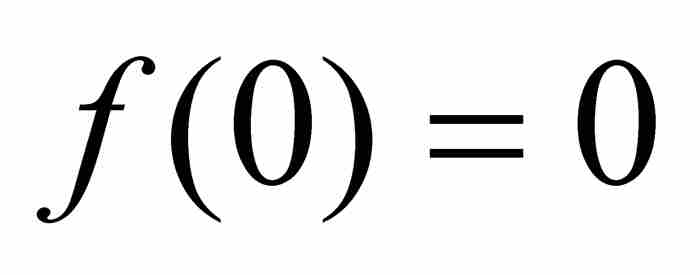 ,因为对于每个k有
,因为对于每个k有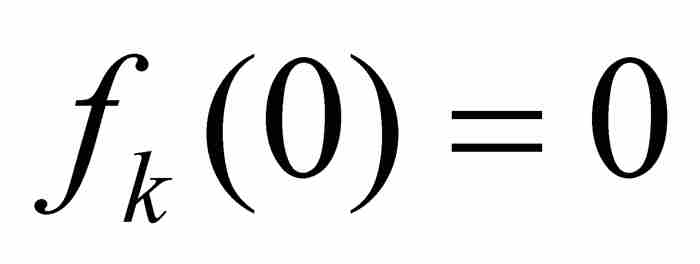 。同时,如果
。同时,如果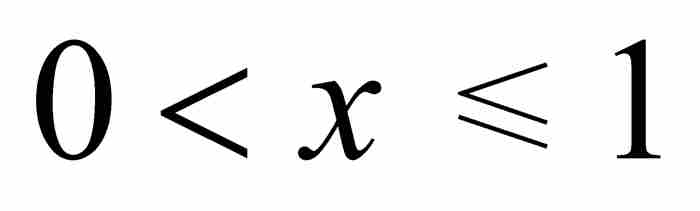 ,我们选择一个满足
,我们选择一个满足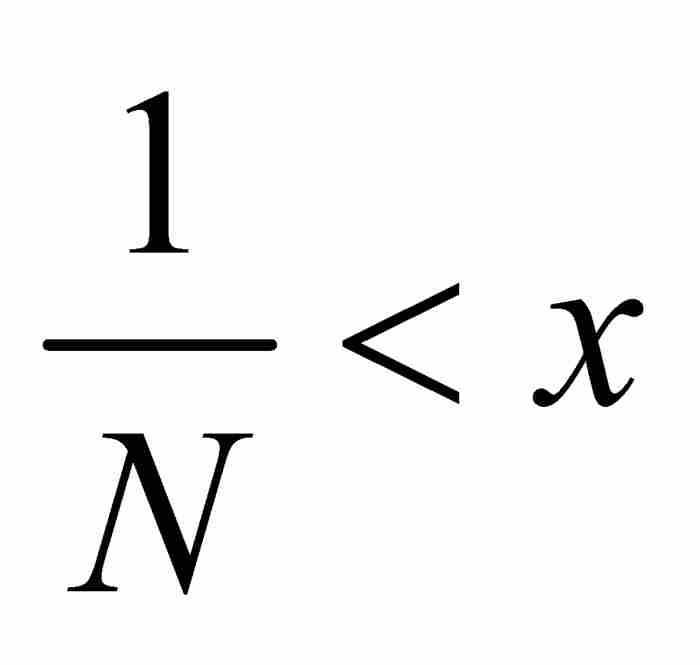 的自然数N,并且考察所有位于其后的函数,即所有满足k≥N的fk,其“尖峰”已经移动到x的左侧,致使
的自然数N,并且考察所有位于其后的函数,即所有满足k≥N的fk,其“尖峰”已经移动到x的左侧,致使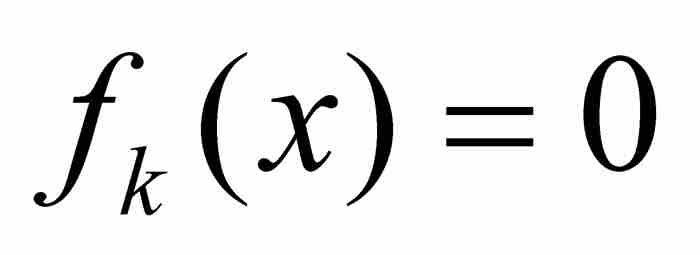 。因此也有
。因此也有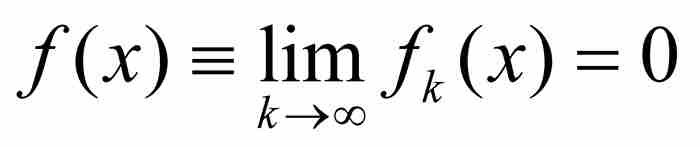 。我们由此看出
。我们由此看出
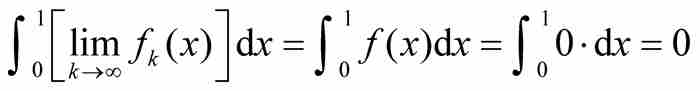
把这个结果同式(2)比较,就显现令人沮丧的事实:函数序列积分的极限不一定等于极限函数的积分。用符号表示,我们得到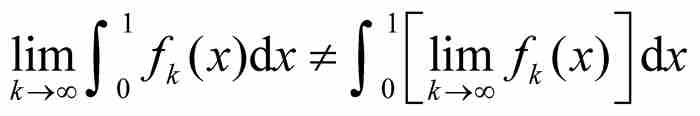 。再次看到,这个函数序列的点态极限不具备一种“优美的”解析特性,这是颇为遗憾的。
。再次看到,这个函数序列的点态极限不具备一种“优美的”解析特性,这是颇为遗憾的。
魏尔斯特拉斯在1841年之前就察觉到这种情况,并且提出一种解决方法。3 但是,以他固有的与众不同的方式,他直到1894年才把自己的思想公诸于世,这已是在半个世纪之后的事情——好在他的学生们很早以前就把这种思想传播出去了。他的想法是引进一种更强的收敛形式,称为一致收敛,在这种收敛概念下,函数序列中个体函数的主要性质将会传递给它的极限函数。
3 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, p. 22。
仿效他的做法,我们给出一致收敛的下述定义:倘若对于每个ε > 0,存在一个自然数N,如果k≥N而x为定义域中的任意点,那么有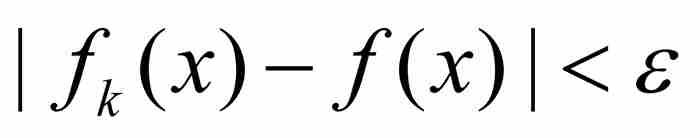 ,这时就说函数序列
,这时就说函数序列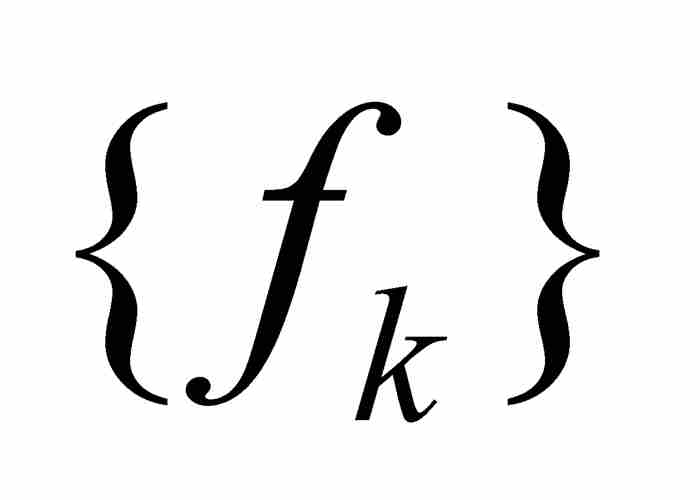 在共同定义域上一致收敛于函数f。联想到一致连续性,这表明在函数
在共同定义域上一致收敛于函数f。联想到一致连续性,这表明在函数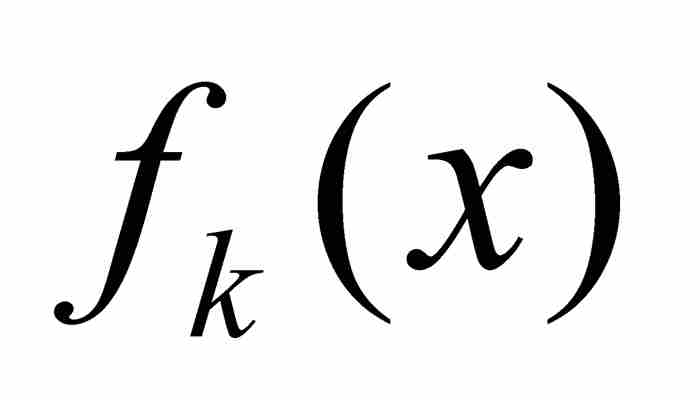 的定义域内“一个N适合于一切x”。
的定义域内“一个N适合于一切x”。
对于这种收敛方式,可以作出几何解释。给定ε > 0,我们画一条包围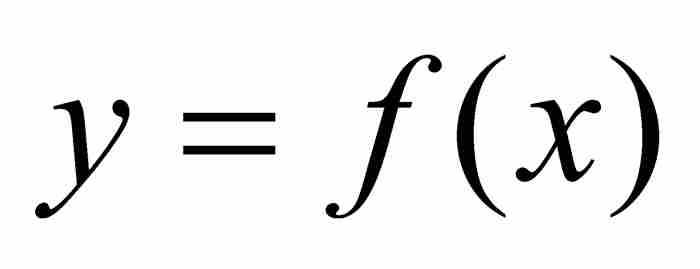 图形的宽度为ε的带状区域,如图9-6所示。依据一致收敛,我们必定达到这样一个下标N,致使序列
图形的宽度为ε的带状区域,如图9-6所示。依据一致收敛,我们必定达到这样一个下标N,致使序列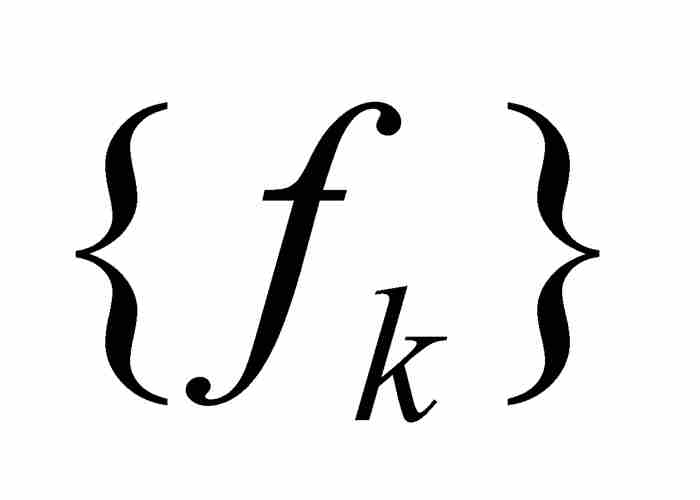 中的fN以及其后的所有函数全部落入这个带状区域。正如一致收敛这个名称所显示的,这样一些函数在区间[a, b]上一致逼近f。
中的fN以及其后的所有函数全部落入这个带状区域。正如一致收敛这个名称所显示的,这样一些函数在区间[a, b]上一致逼近f。
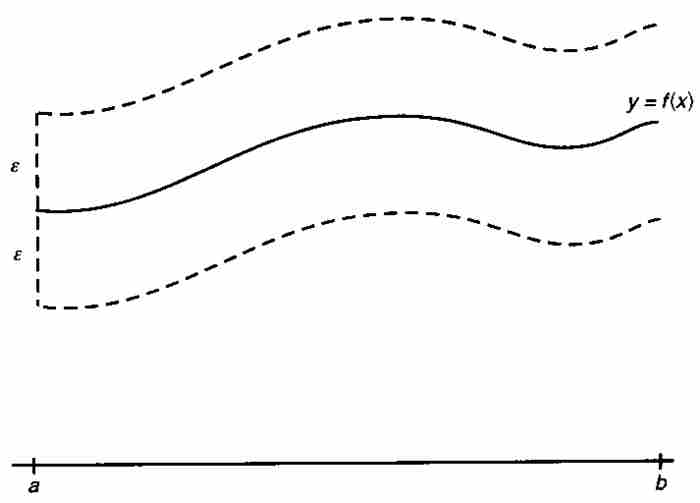
图 9-6
不难看出,如果一个函数序列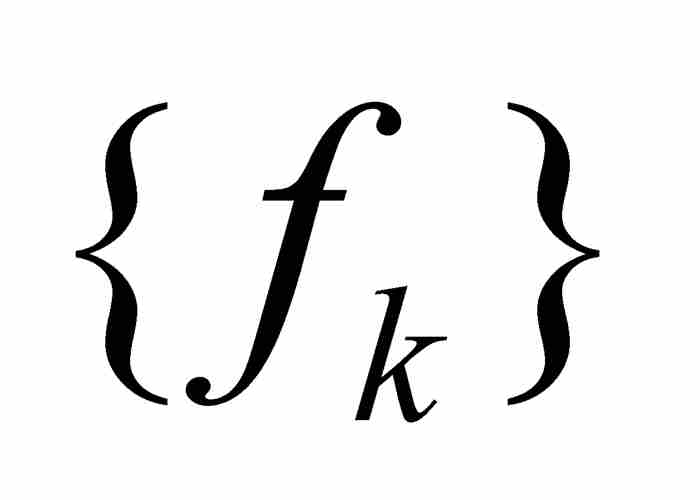 一致收敛于函数f,那么
一致收敛于函数f,那么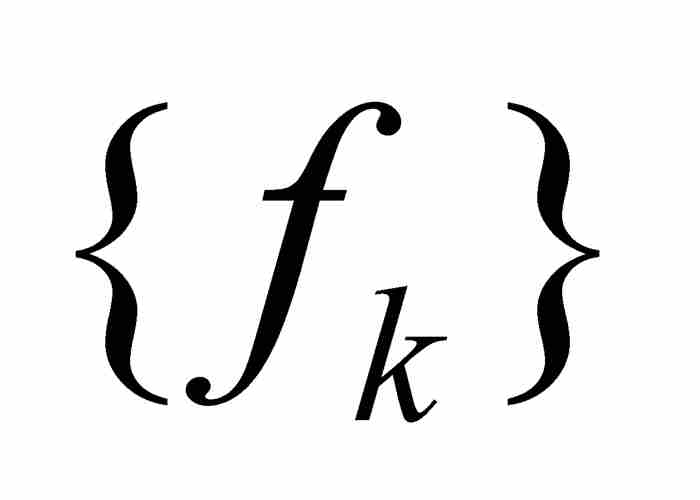 点态收敛于f,但是相反的命题不成立。例如,前面描述的“尖峰”函数序列在区间[0, 1]上点态收敛于零值函数,但是不一致收敛于零值函数。同仅仅是点态收敛相比,一致收敛算是一种更强的和限制更大的收敛形态。
点态收敛于f,但是相反的命题不成立。例如,前面描述的“尖峰”函数序列在区间[0, 1]上点态收敛于零值函数,但是不一致收敛于零值函数。同仅仅是点态收敛相比,一致收敛算是一种更强的和限制更大的收敛形态。
出于几点原因,我们在这里脱离了主题。首先,在本章的主要结果中需要用到一致收敛的概念。其次,这些思想在本书其余部分反复出现。最后,这样一些成熟的见解足以说明,在微积分的历史上魏尔斯特拉斯何以占有如此重要的地位。Victor Katz对于他的工作作出这样的评价:
在魏尔斯特拉斯给出的定义中,他不仅绝对清楚某些量是如何依赖于其他量的,而且完成了不用像“无穷小”这样一些术语的转变。从此以后,凡是涉及这类概念的定义,全部都是用算术方式给出的。4
4 Victor Katz, A History of Mathematics: An Introduction, Harper-Collins, 1993, p. 657。
四个重要定理
魏尔斯特拉斯不仅重新审视分析学中的各种定义,同时他还是应用它们证明重要定理的大师。下面我们给出他获得的四个涉及一致收敛的结果,不过不予证明。
前面两个定理解决上面提及的一个题目:在一致收敛条件下,函数的重要的解析性质从函数序列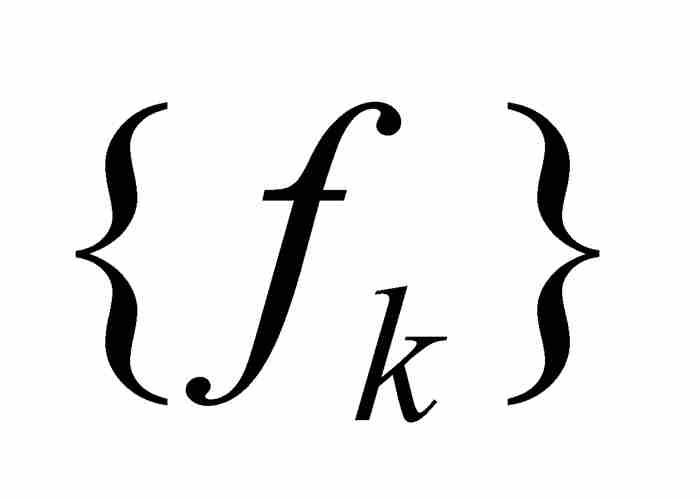 的个体项传递给它们的极限函数f。
的个体项传递给它们的极限函数f。
定理 1 如果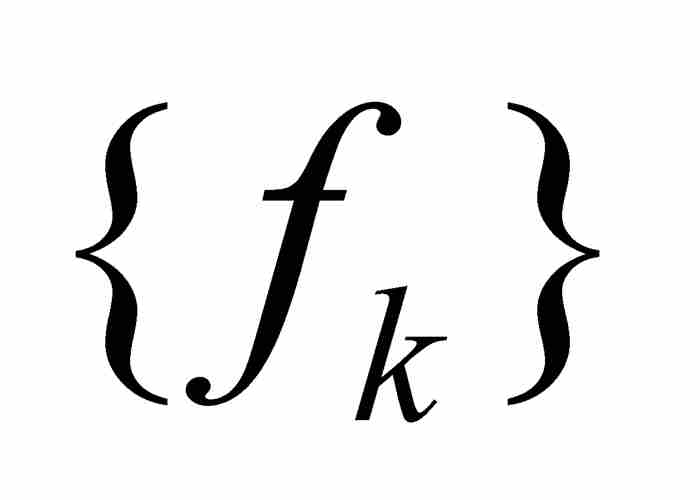 是在区间[a, b]上一致收敛于f的连续函数的序列,那么f本身也是连续函数。
是在区间[a, b]上一致收敛于f的连续函数的序列,那么f本身也是连续函数。
定理 2 如果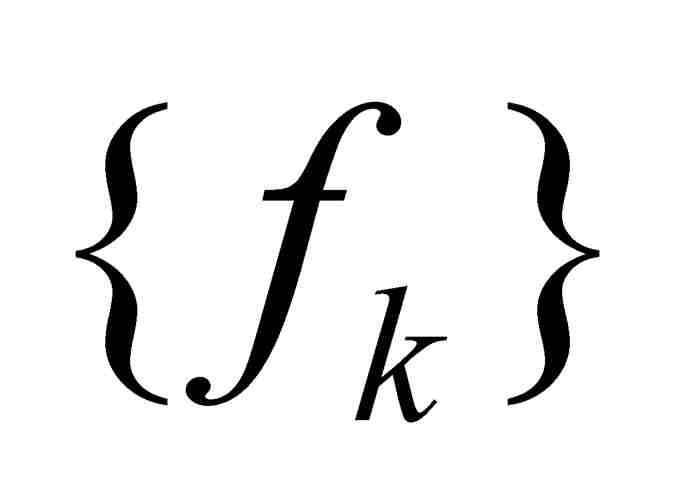 是在区间[a , b]上一致收敛于f的有界黎曼可积函数的序列,那么f在[a, b]上是黎曼可积的,并且
是在区间[a , b]上一致收敛于f的有界黎曼可积函数的序列,那么f在[a, b]上是黎曼可积的,并且
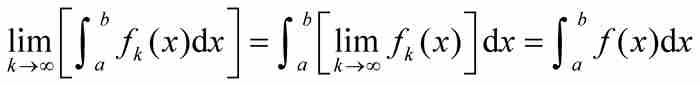
根据定理2,对于一致收敛的函数序列,允许进行取极限与求积分的交换。
第三个定理如今称为魏尔斯特拉斯逼近定理。这个定理在连续函数同多项式之间提供一种始料未及的联系。
定理 3(魏尔斯特拉斯逼近定理) 如果f是定义在有界闭区间[a, b]上的连续函数,那么存在一个在[a, b]上一致收敛于f的多项式的序列{Pk}。
这个定理如此令人着迷,原因在于有的连续函数可能是特性极差的(事实上,这正是我们马上要考察的魏尔斯特拉斯反例的特点)。相比之下,多项式却是非常平和的函数。后者竟然可能一致逼近前者,这仿佛是一桩奇妙的天赐良缘。
这三个定理都与一致收敛有关。它们使连续性和可积性从函数序列的个体函数传递给它们的极限函数,并且提供一种用多项式逼近连续函数的手段。但是首先要问,存在确定一致收敛的简单方法吗?
判别一致收敛的一种途径是用所谓的魏尔斯特拉斯M检验法,这是我们初步结果中的最后一个定理。像前面那样,我们从在一个共同定义域上定义的函数序列{ fk}开始,不过M检验法引进一种新奇的方法:我们把序列的前n项相加,建立部分和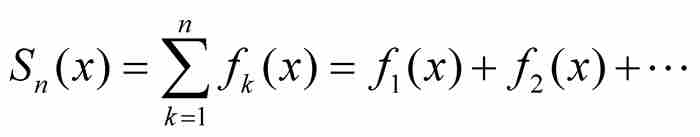
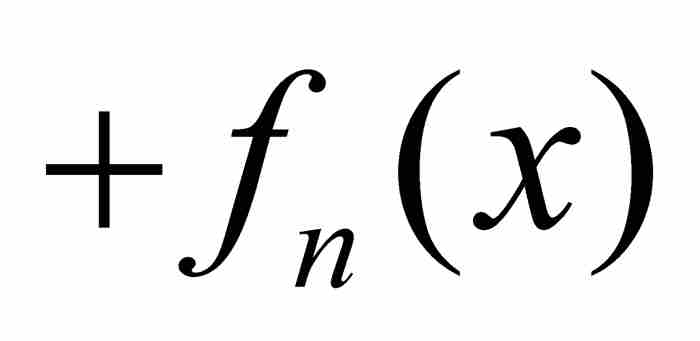 。如果部分和的序列{Sn}一致收敛于一个函数f,我们就说函数项的无穷级数
。如果部分和的序列{Sn}一致收敛于一个函数f,我们就说函数项的无穷级数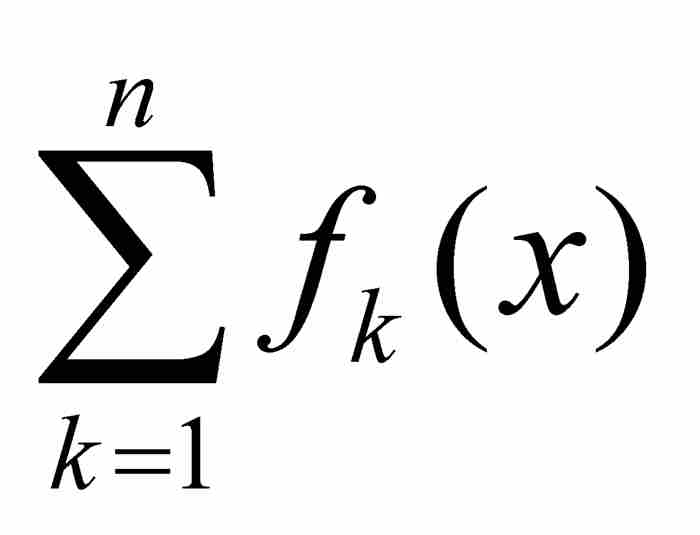 一致收敛于f (x)。在这个基础上,现在我们来陈述下述结果。
一致收敛于f (x)。在这个基础上,现在我们来陈述下述结果。
定理 4(魏尔斯特拉斯M检验法) 设{fk (x)}是定义在一个共同定义域上的函数序列。如果对于每个k,存在一个正数Mk,使得对于定义域内的所有x,有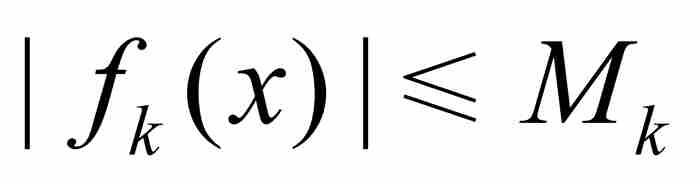 ,并且如果无穷级数
,并且如果无穷级数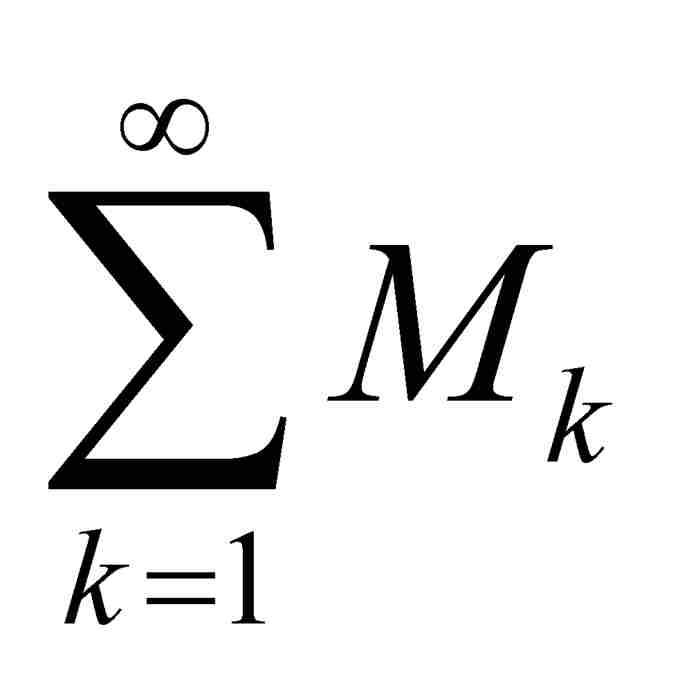 收敛,那么函数项级数
收敛,那么函数项级数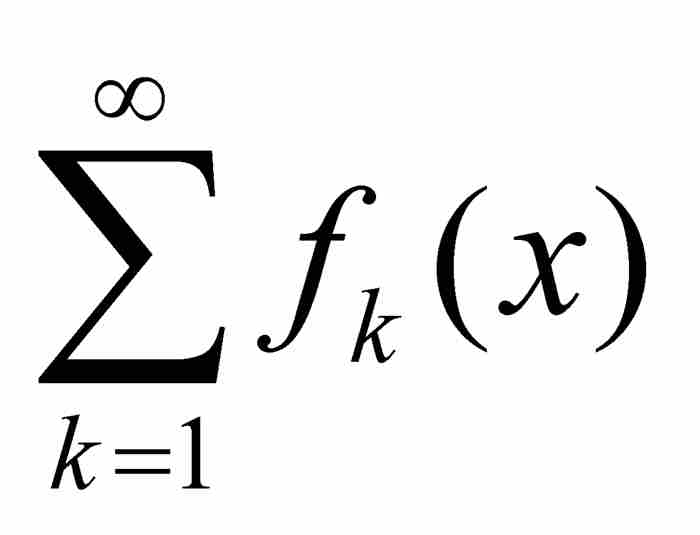 一致收敛。
一致收敛。
这个检验法相当于函数级数与数值级数之间的一个比较检验法,其中数值级数的收敛蕴含函数级数的一致收敛。例如,考虑区间[0,1]上由
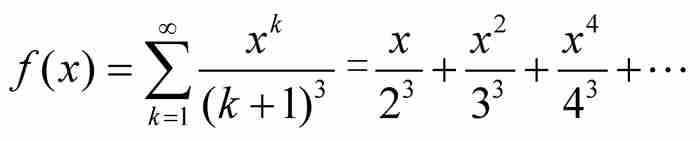
定义的函数。这里,对于[0, 1]内的所有x,我们有| fk(x)|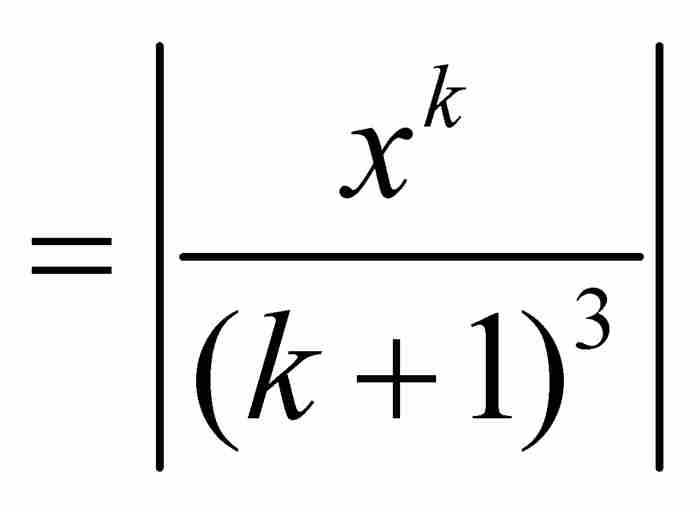
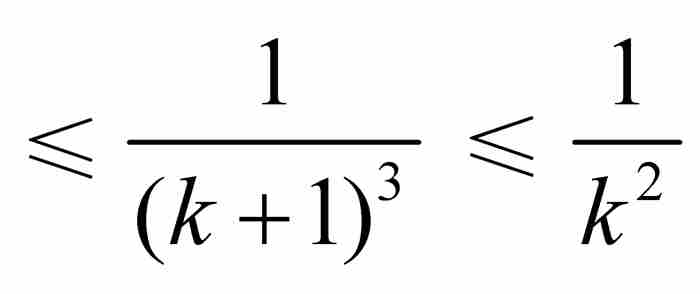 ,而根据第4章欧拉关于雅各布·伯努利难题的结果,可知
,而根据第4章欧拉关于雅各布·伯努利难题的结果,可知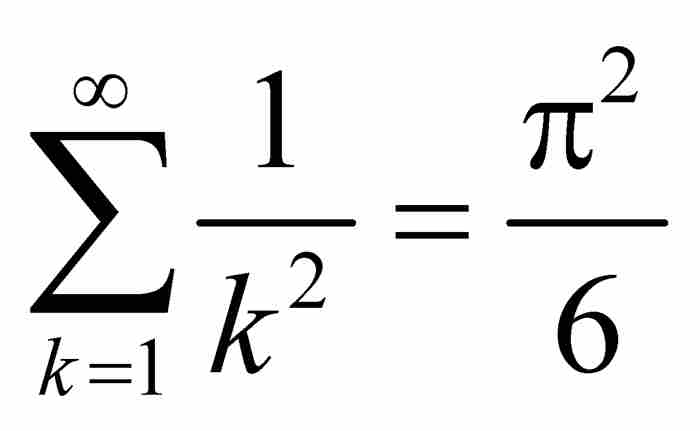 。由M检验法立即推出函数f (x) 一致收敛。此外,如果对部分和Sn(x)应用定理1和定理2,可知f本身也是连续函数,因为每个部分和函数是连续的,并且
。由M检验法立即推出函数f (x) 一致收敛。此外,如果对部分和Sn(x)应用定理1和定理2,可知f本身也是连续函数,因为每个部分和函数是连续的,并且
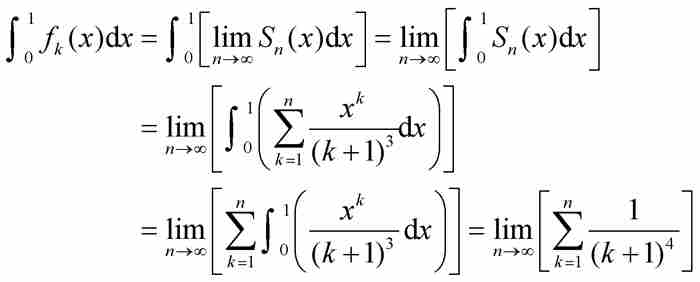
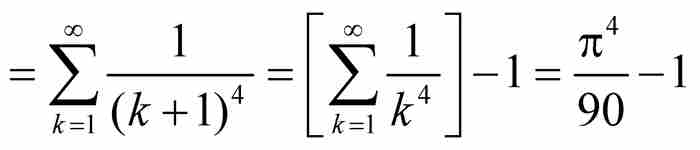
其中再次得益于欧拉关于级数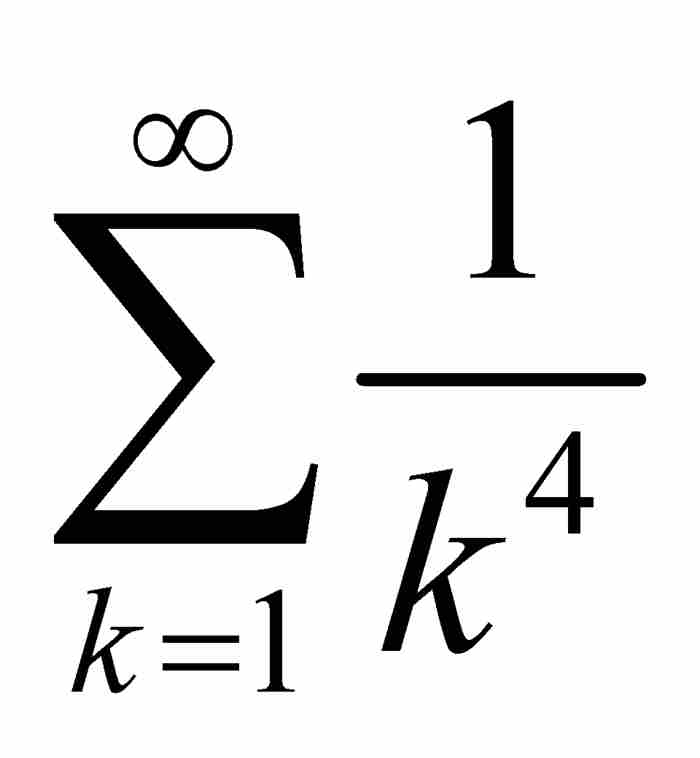 的结果。至此,对于交换取极限与求积分的无限过程,无论情况多么复杂,我们已经提示所有的干预步骤。魏尔斯特拉斯M检验法使我们能够断定f (x)是连续函数,并且准确地求出它的积分值,这是一个具有重大意义的成就。
的结果。至此,对于交换取极限与求积分的无限过程,无论情况多么复杂,我们已经提示所有的干预步骤。魏尔斯特拉斯M检验法使我们能够断定f (x)是连续函数,并且准确地求出它的积分值,这是一个具有重大意义的成就。
我们终于完成了一切准备工作,搭建起数学史上行将演绎的一个轰动事件的舞台。
魏尔斯特拉斯病态函数
数学家们早就知道,一个可微的(“光滑的”)函数必定是连续的(“不间断的”)函数,但是,反之不然。例如,一个像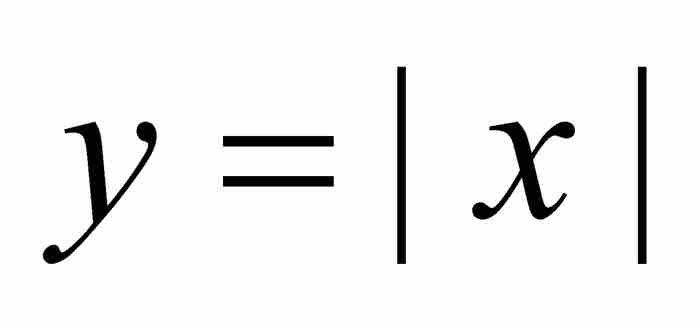 这样的V字型函数是处处连续的函数,但是它在x = 0处是不可微的,它的图形在那里突然改变方向,形成一个拐角。
这样的V字型函数是处处连续的函数,但是它在x = 0处是不可微的,它的图形在那里突然改变方向,形成一个拐角。
然而,人们曾经认为连续函数必定“多半”是光滑的。赫赫有名的安德烈·马里·安培(1775—1836)对连续函数通常是可微的命题曾经提出过一个证明,而且在19世纪整个前半期,微积分学教科书都支持这种见解。1
1 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 43-44。
这无疑是有吸引力的。任何人可以想象这样一幅连续的“锯齿”状图形,平滑地上升到一个齿角,然后下降到下一个齿角,接着再上升到另一个齿角,如此延续下去。当我们压缩“锯齿”时,得到越来越多不可微的点。尽管如此,似乎必定继续存在使函数图形从一个齿角平滑地上升或者下降到另一个齿角的区间。由此可见,几何图形表明,任何连续函数必定存在大量可微的点。
因此,当魏尔斯特拉斯构造出处处连续但是无处可微的函数时,引起巨大震惊,这是一个稀奇古怪的函数实体,它看起来是连续的,却是处处参差不齐的。这个函数被大多数人视为难以想象的,它不仅推翻了安培的“定理”,而且把几何直观作为微积分的可靠基础的主张逐出了历史舞台。
人们普遍认为,魏尔斯特拉斯是在19世纪60年代构造出他的例子的,并且在1872年7月18日把这个例子提交给柏林科学院。按照以往的习惯,魏尔斯特拉斯没有匆忙公布他的发现;直到1875年,这个病态函数才由保罗·杜布瓦·雷蒙(1831—1889)首次发表。
毋庸置疑,一个如此特殊的函数自然远非初等函数。就其学术上的复杂程序而言,它或许是本书中要求最苛刻的结果。但是,由于这个函数独具的违反直觉的特性,努力构造它是非常值得的,更不用说它具有的历史意义了。下面我们仿效魏尔斯特拉斯的论证,但是改变了他的记号,同时为了清晰起见,间或添加了某些细节。
我们从一个引理开始,这个引理是魏尔斯特拉斯在证明中需要使用的。他用一个三角恒等式证明这个引理,但是我们给出利用微积分的一个证明。
引理 如果B > 0,那么
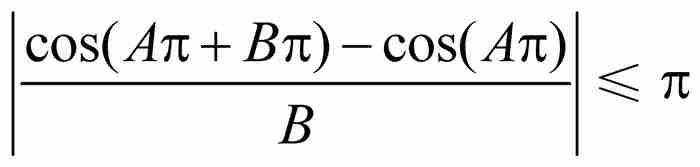
证明 令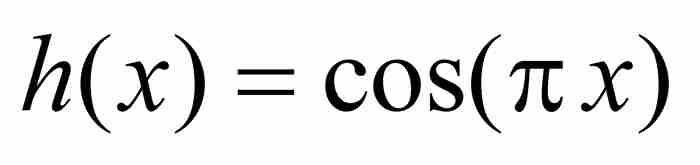 是区间[A, A + B]上的函数。根据中值定理,在A和A + B之间存在一点c,使得
是区间[A, A + B]上的函数。根据中值定理,在A和A + B之间存在一点c,使得
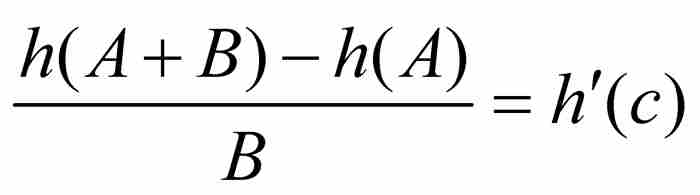
这个结果等价于
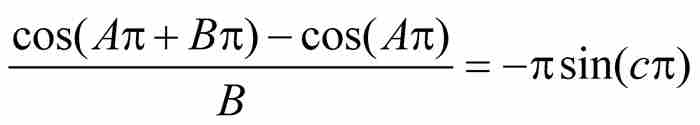
由此推出
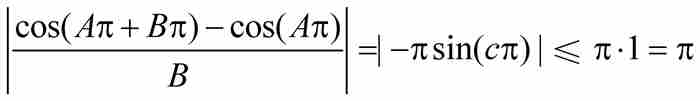
现在我们用魏尔斯特拉斯本人当初的表达方式介绍他的著名反例。
定理 如果 a ≥ 3 是一个奇数,b是严格介于0与1之间的一个常数且满足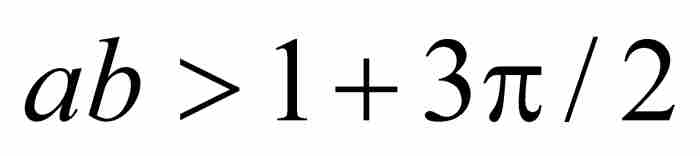 ,那么函数
,那么函数
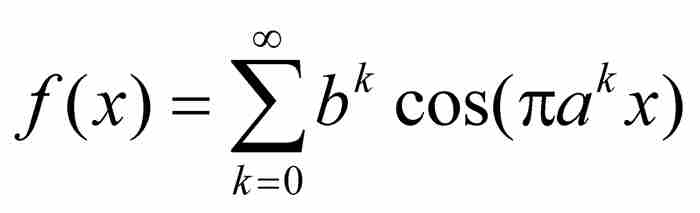
是处处连续的和无处可微的。2
2 Karl Weierstrass, Mathematische Werke, vol. 2, Berlin, 1895, pp. 71-74。

魏尔斯特拉斯病态函数(1872)
证明 显然,魏尔斯特拉斯在对a和b设置这些离奇的约束条件之前,已经进行了大量收集材料的准备工作。为了简化讨论,我们将取a = 21和b = 1/3。这种选择满足定理中设定的条件,因为 a ≥ 3 是一个奇数,b位于区间(0, 1)内,并且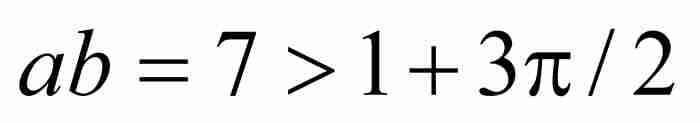 。所以,我们的特定函数将是
。所以,我们的特定函数将是
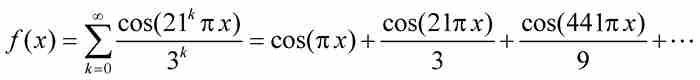 (3)
(3)
为了证明f的连续性,只需应用M检验法。显而易见,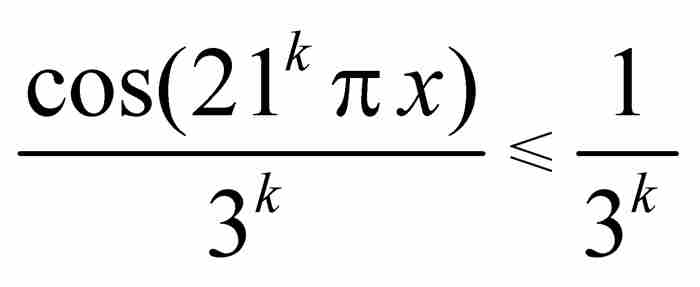 ,而
,而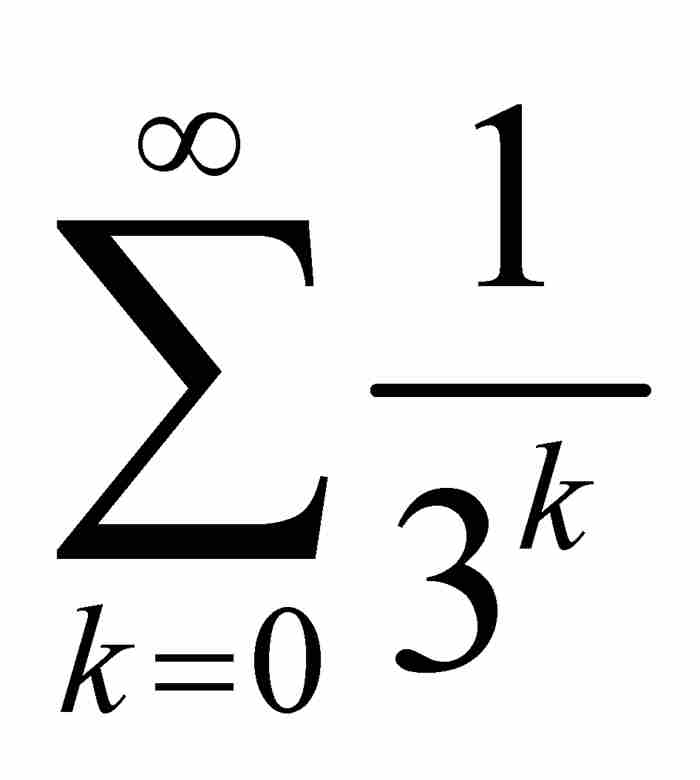 收敛于3/2。因此,这个级数一致收敛于f。由于每个直和项
收敛于3/2。因此,这个级数一致收敛于f。由于每个直和项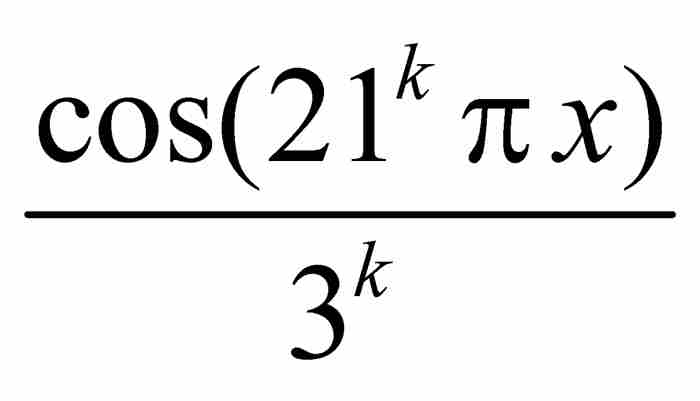 是处处连续的,所以根据前面的定理1,f也是处处连续的。
是处处连续的,所以根据前面的定理1,f也是处处连续的。
对于证明函数f是处处连续的和无处可微的,看起来我们已做了一半工作,然而,证明它是“无处可微的”部分却是难上加难的。为此目的,我们从固定一个实数r开始。我们的目标在于证明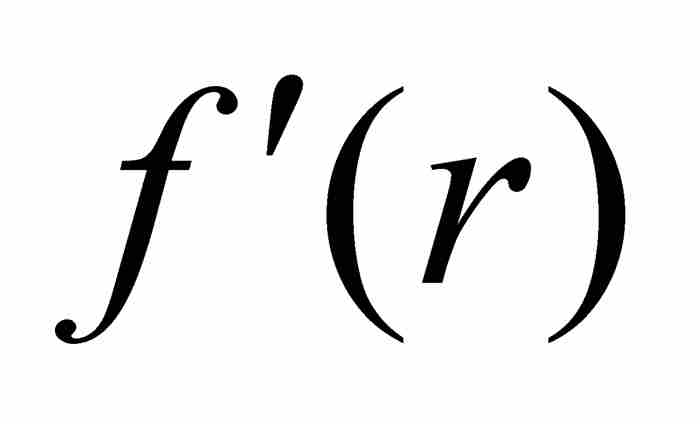 是不存在的。由于r是任意的,这个结果也就证实f无论在什么点都是不可微的。
是不存在的。由于r是任意的,这个结果也就证实f无论在什么点都是不可微的。
在下述魏尔斯特拉斯推理中,汇集一些看上去没有联系的问题的若干结果是有益的。毫无疑问,其中每个结果都会在他的盛大演出的某个场合扮演重要角色。
首先,魏尔斯特拉斯注意到,对于每个m = 1, 2, 3, …,实数21 mr(像任何实数一样)处于同它最接近的整数的半个单位的范围内。因此,对于每个整数m,存在这样一个整数αm,使得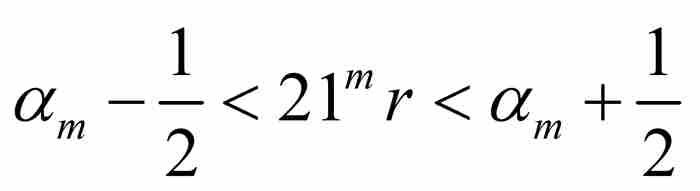 (参见图9-7)。令
(参见图9-7)。令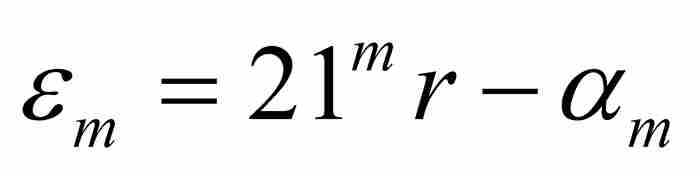 为
为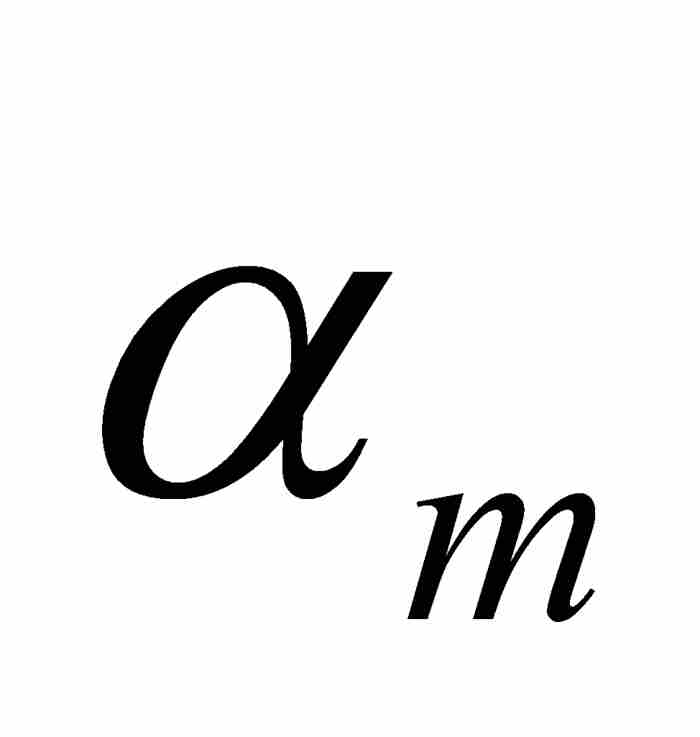 同21 mr之间的间距,我们看出
同21 mr之间的间距,我们看出
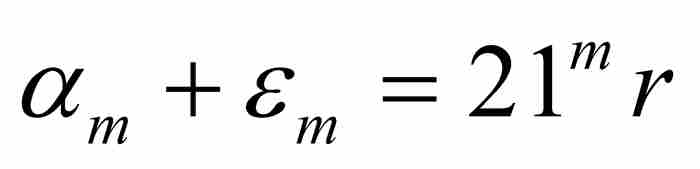 (4)
(4)

图 9-7
由于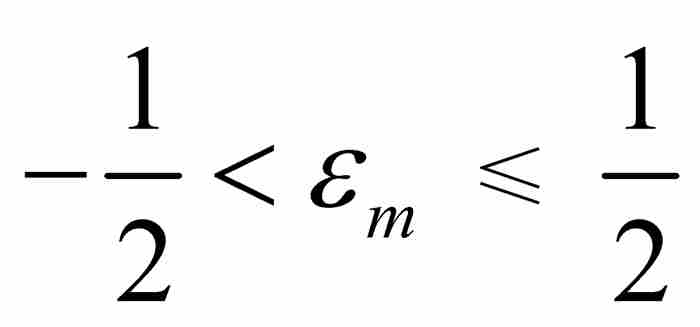 ,所以
,所以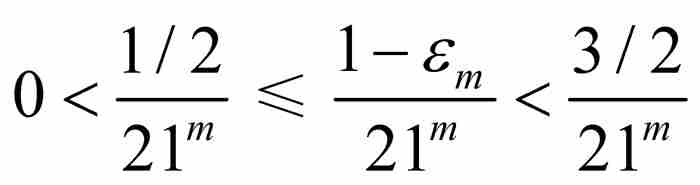 。为了便于表示,我们引入
。为了便于表示,我们引入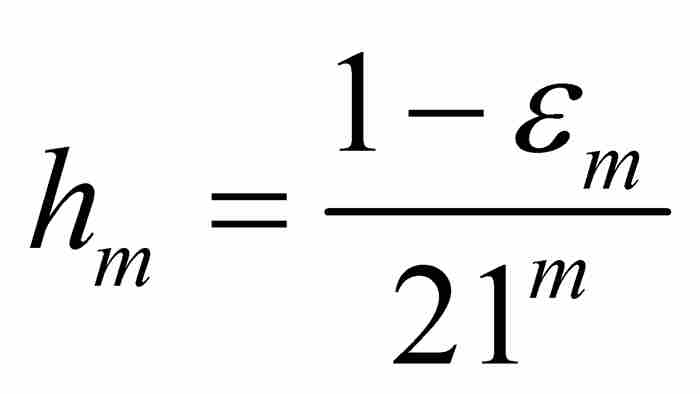 ,并且注意
,并且注意
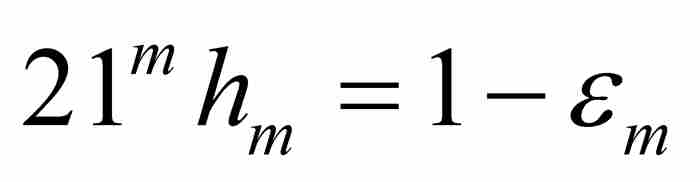 和
和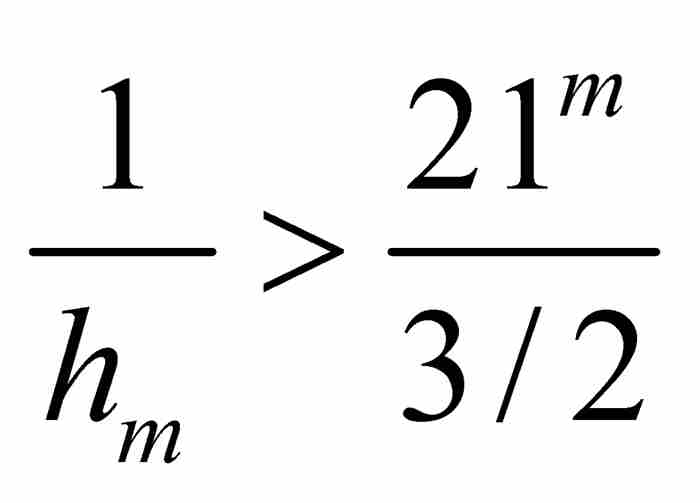 (5)
(5)
现在,根据挤压定理,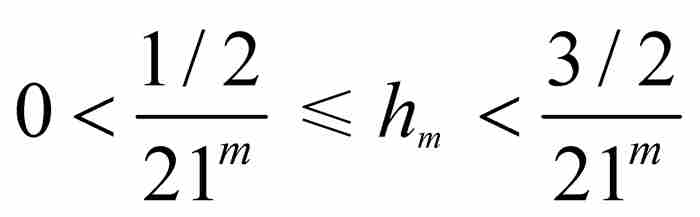 足以保证
足以保证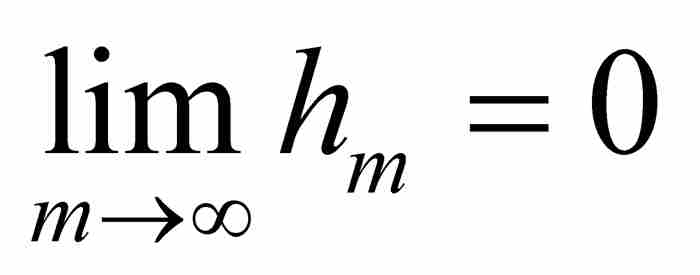 。这个正数项序列将在证实f (x)的不可微性中起决定性作用。
。这个正数项序列将在证实f (x)的不可微性中起决定性作用。
这时,我们(暂且)固定整数m。像魏尔斯特拉斯所做的那样,我们利用式(3),并且考察微商:
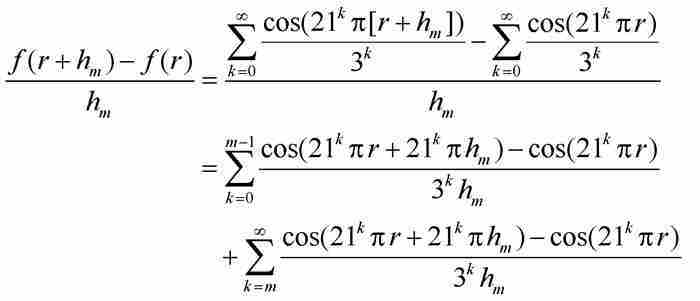
(6)
在此,无穷级数已经被分成两部分。魏尔斯特拉斯将分别考察每一部分的绝对值。
对于第一个级数,我们应用引理,并取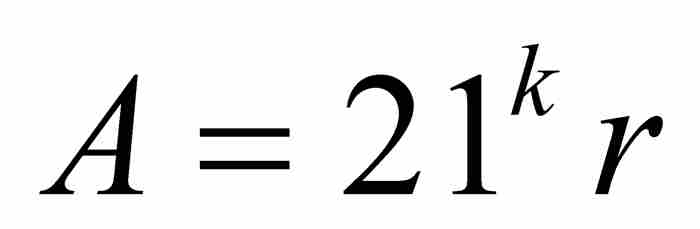 和
和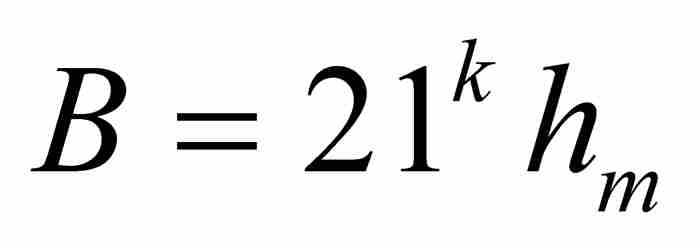 ,确定每个直和项的界如下:
,确定每个直和项的界如下:
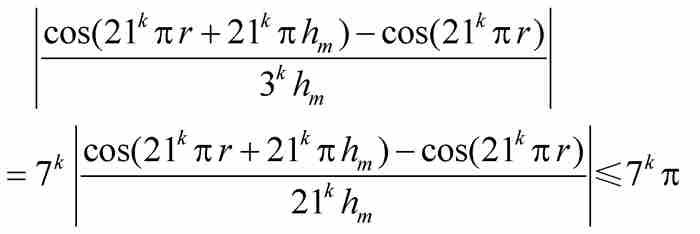
于是,由三角不等式,我们得到第一个级数的一个上界:
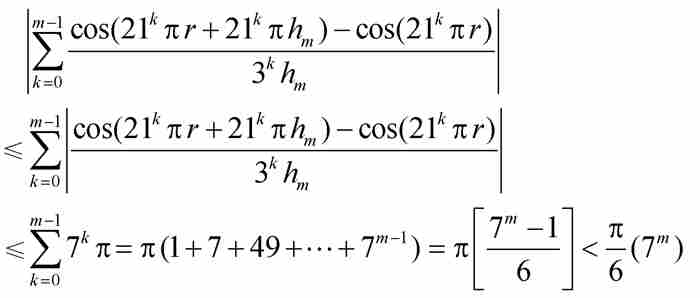
(7)
式(6)中的第二个级数提出一个更大的挑战。为了确定它的绝对值,我们进行四项相关的考察:
(A)如果k≥m,由式(4)和式(5)看出
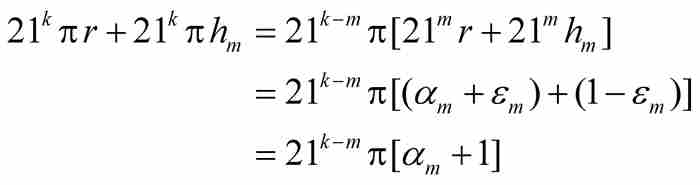
但是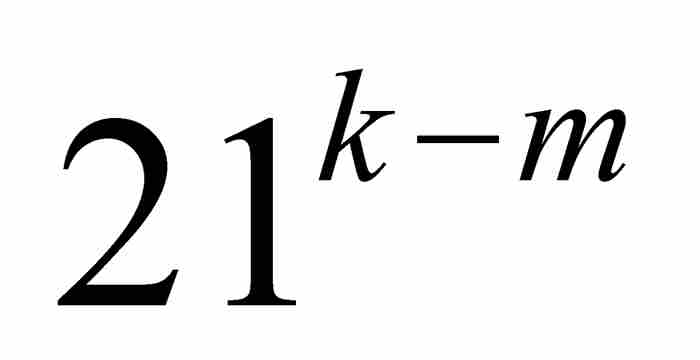 是一个奇数,而αm也是一个整数。因此,
是一个奇数,而αm也是一个整数。因此,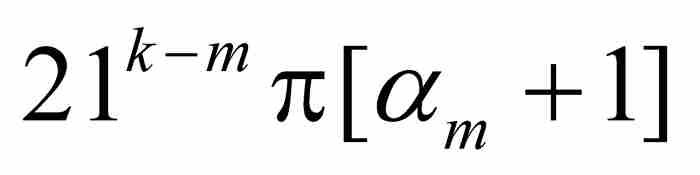 等于 π 的偶数倍或者奇数倍,这取决于
等于 π 的偶数倍或者奇数倍,这取决于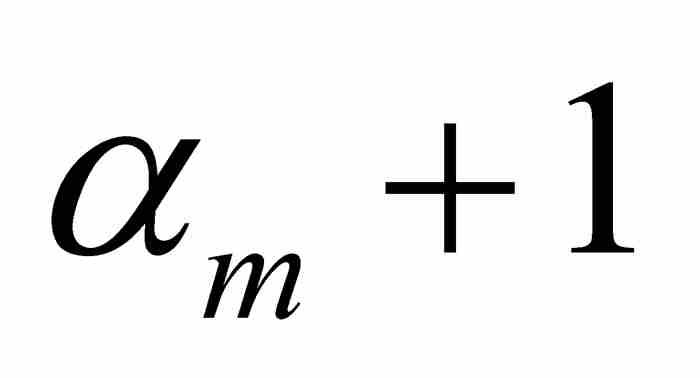 为偶数或者奇数。由此推出
为偶数或者奇数。由此推出
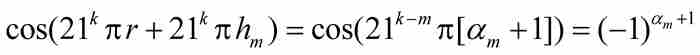
(B)我们再限定k≥m,并且利用式(4),得到
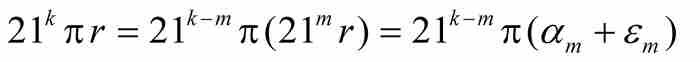
由一个众所周知的三角恒等式,我们得到
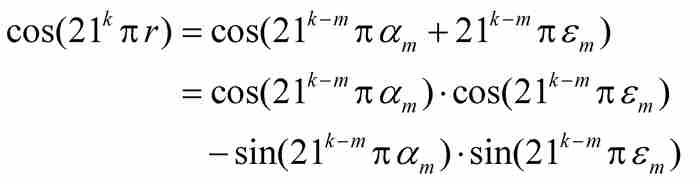
此处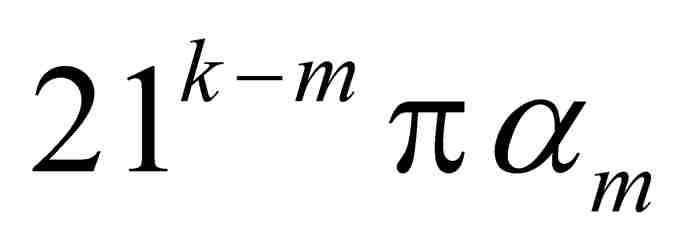 等于π的偶数倍或者奇数倍,这取决于
等于π的偶数倍或者奇数倍,这取决于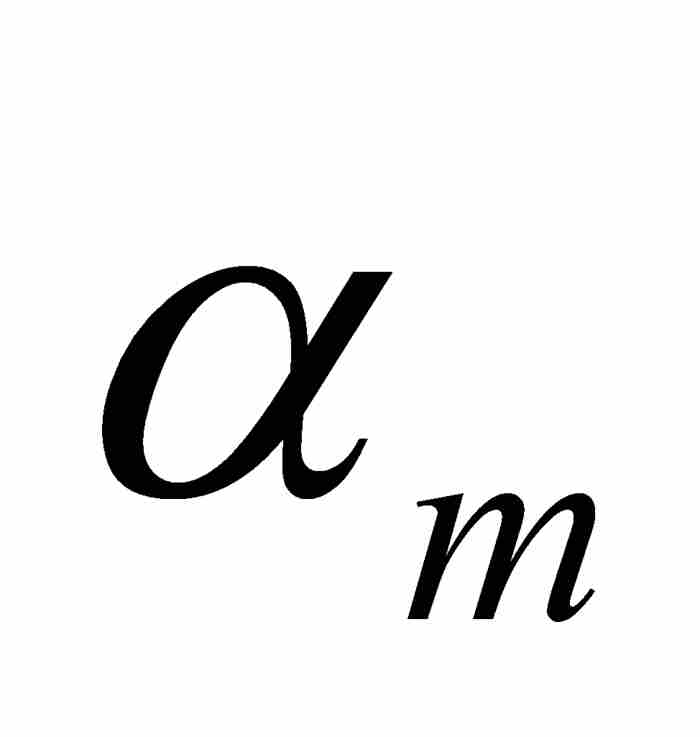 为偶数或者奇数,所以
为偶数或者奇数,所以
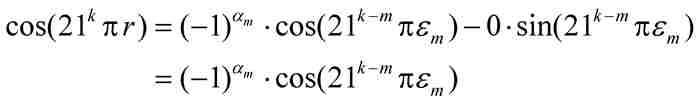
(C)(这是一项容易求得的结果)由于余弦的性质,
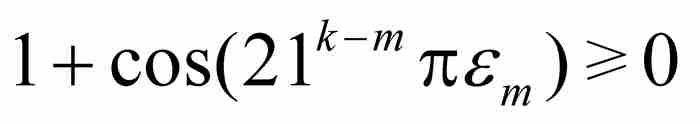
(D)由于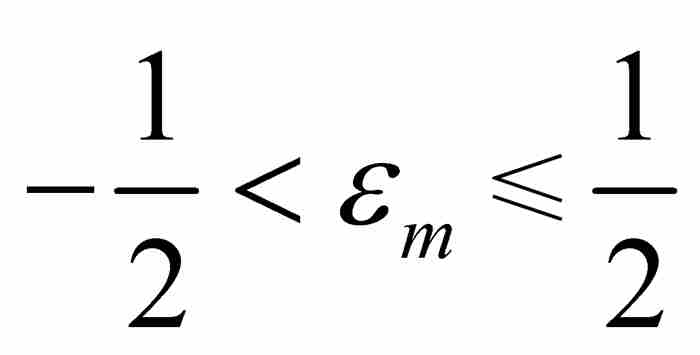 ,可知
,可知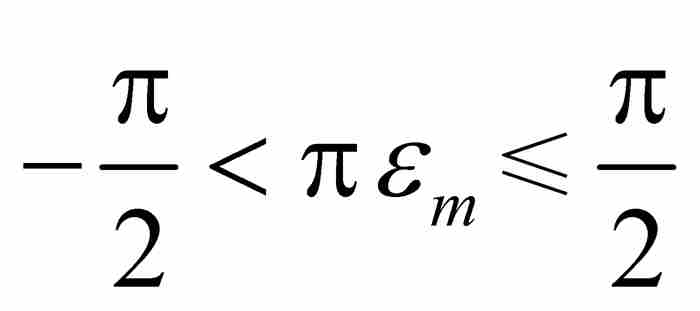 ,所以
,所以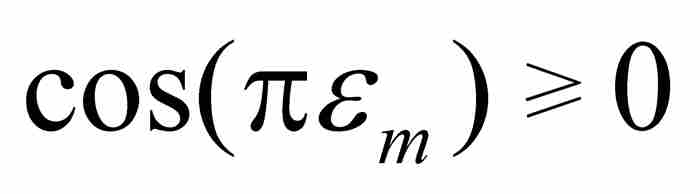 。
。
现在,对于式(6)中第二个级数应用(A)和(B)的结果,得到它的绝对值的一个下界:

最后一个等式成立是因为根据(C),级数中的每一项取非负值。
这个非负项级数的和必定大于它的第一项(其中k = m),所以根据(D)和式(5),我们得到
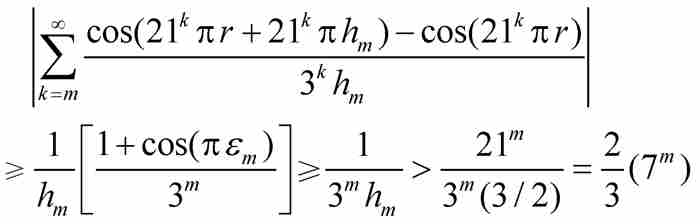
以上全部推导,落下了正剧之前的冗长序幕。魏尔斯特拉斯此时导出了关键性的不等式,他从刚才证明的结果开始,最终确定函数f (x)的微商的界限:
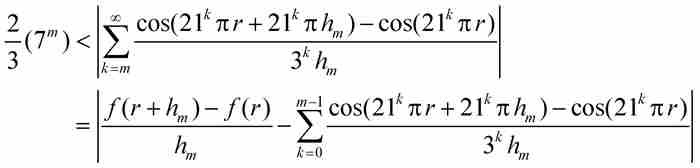
(根据式(6))
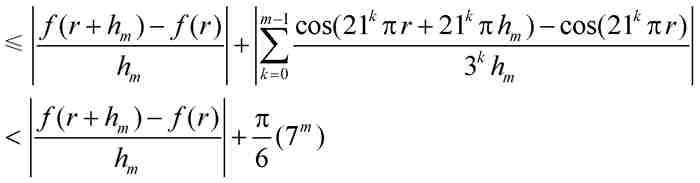
(根据式(7))
从这一串不等式中的第一个和最后一个,我们推出
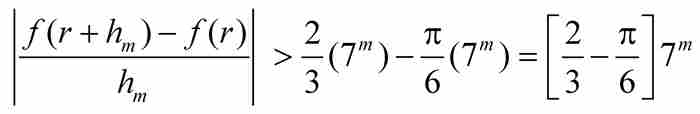 (8)
(8)
表达式(8)具有两个主要特性:第一,数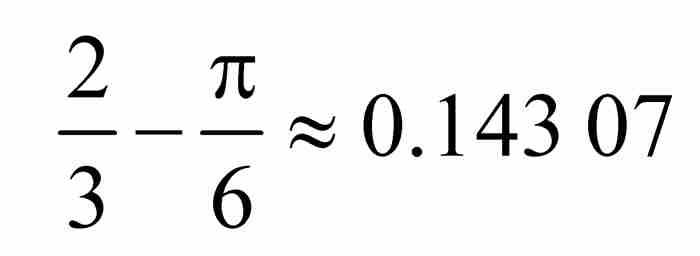 是一个正常数。第二,式(8)中的不等式对于我们所取的固定的自然数m成立,而m是随意取的。考虑到这一点,我们现在“不固定”m,并且取极限:
是一个正常数。第二,式(8)中的不等式对于我们所取的固定的自然数m成立,而m是随意取的。考虑到这一点,我们现在“不固定”m,并且取极限:
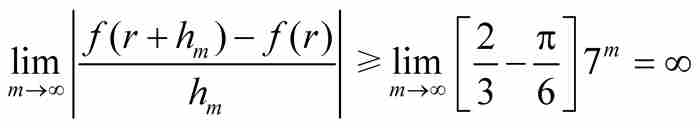
但是我们注意到,当 时
时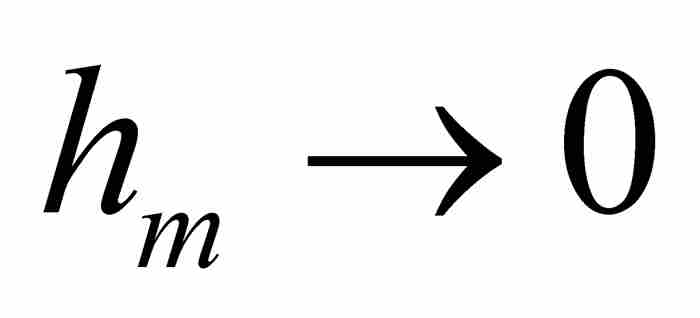 。因此,
。因此,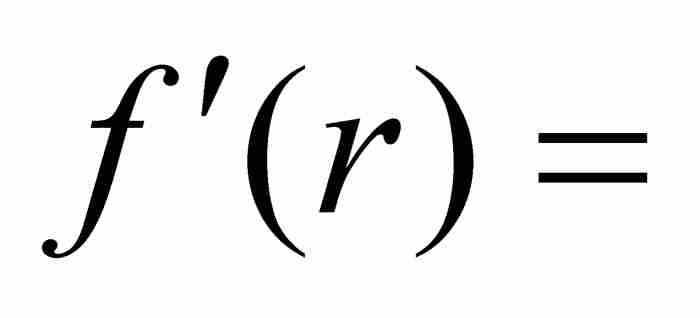
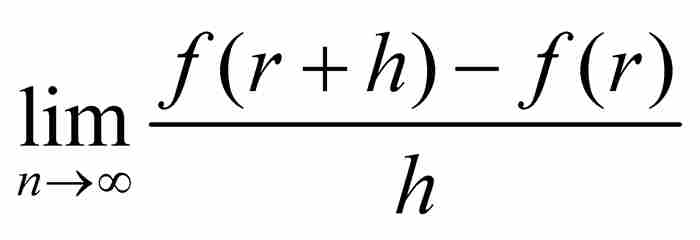 不能作为一个有限量存在。简单地说(简单吗?)
不能作为一个有限量存在。简单地说(简单吗?)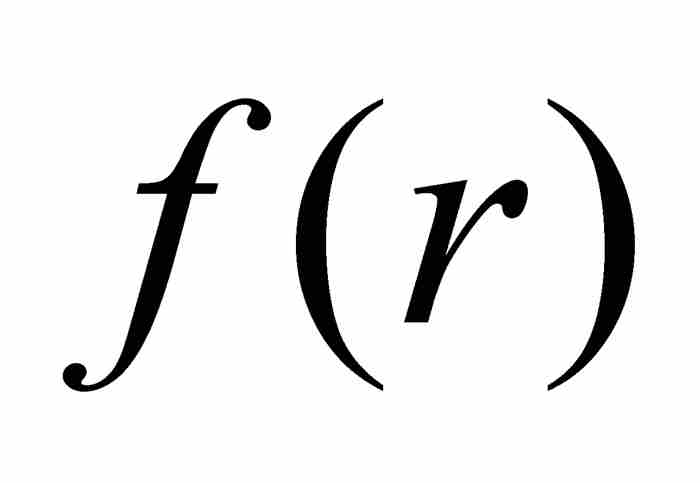 在x = r是不可微的。同时,由于r是一个未指定的实数,这就证实魏尔斯特拉斯定义的函数是无处可微的,尽管它是处处连续的函数。
在x = r是不可微的。同时,由于r是一个未指定的实数,这就证实魏尔斯特拉斯定义的函数是无处可微的,尽管它是处处连续的函数。
当读者从魏尔斯特拉斯论证的震撼下恢复平静时,多半会产生一些反应。反应之一会是对他所表现的才能万分惊讶。他在整合这个证明中显示出的天赋是出类拔萃的。
另一个反应是可能产生某种不安的感觉,因为我们恰好证实了一个连续函数可以不存在可微性点。函数的图形无处是平滑地上升的或者下降的。在它的图形上没有一点存在一条切线。这是一个离奇的函数,它的每个点好似一个尖角,然而它又是处处连续的。
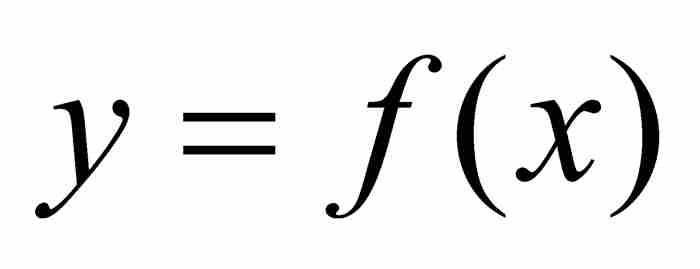 的图形是否会给我们一些启发呢?很遗憾,由于f是函数项的一个无穷级数,我们只能停留于画出部分函数和的图形。例如,我们在图9-8中仅画出第3个部分和
的图形是否会给我们一些启发呢?很遗憾,由于f是函数项的一个无穷级数,我们只能停留于画出部分函数和的图形。例如,我们在图9-8中仅画出第3个部分和
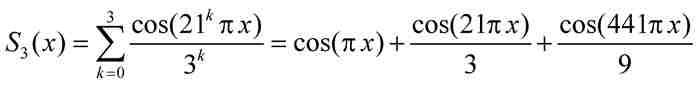
的图形。这个图形显示出大量的方向改变以及某种急剧上升和下降的特性,但是没有尖角。事实上,魏尔斯特拉斯函数的任何部分和只包含有限的余弦项,因而是处处可微的。无论画出哪个部分和的图形,我们都不能从中找到一个角点。然而,当我转向求极限产生f本身时,必定处处出现角点。魏尔斯特拉斯函数超出我们直觉所能理解的范围,是远非可以用几何图形画在黑板上的。但是从上面的证明看出,它的存在是毋庸置疑的。
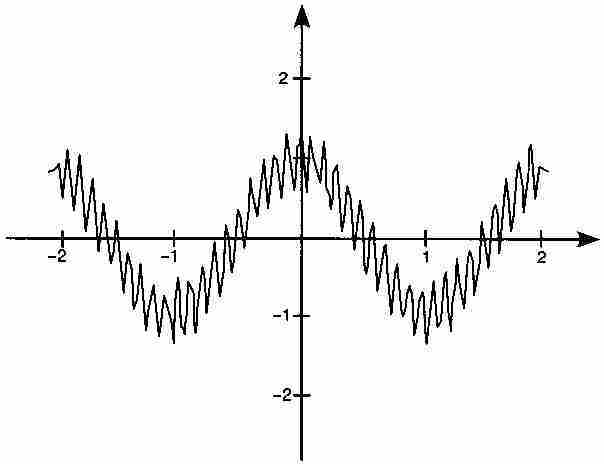
图 9-8
对于魏尔斯特拉斯这个论证的最后一个反应必然是为它的高度严格的标准喝采。犹如一位音乐大师指挥一支著名的管弦乐队,魏尔斯特拉斯把基本定义、绝对值以及大量的不等式融合成一个协调的整体。在他的证明中,看不出任何处理是随心所欲的,不存在丝毫凭直觉的痕迹。所以后代的分析学家们对他的最高赞誉是这个证明展现了“魏尔斯特拉斯的严格性”。
毫无疑问,对于一个如此病态的函数,并非人人都会感到兴奋。某些批评者毅然反对存在一个把不等式作为对付直觉的王牌的数学世界。我们在前面一章介绍过的查尔斯·埃尔米特,对于这个发现黯然神伤,哀叹道:“从这场令人惋惜的没有导数的函数灾难中,我深感震惊和恐怖”。3 亨利·庞加莱(1854—1912)把魏尔斯特拉斯举出的病态函数的例子称为“一种对常识的蹂躏”。4 受到的触怒的埃米尔·皮卡(1856—1941)则这样表达他的愤慨:“要是牛顿和莱布尼茨曾经想到连续函数不一定存在导数,…… 他们就无需发明微分法了。” 5 不过,这些仿佛从伊甸园走出来的数学家信以为真的建立在直觉形式和几何基础上的微积分已经永远消失了。
3 引自Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 973。
4 E. Hairer and G. Wanner, Analysis by Its History, Springer- Verlag, 1996, p. 261。
5 引自Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 1040。
但是,魏尔斯特拉斯的推理是严密的。只要不抛弃极限、连续性和可微性的定义,或者不拒绝赋予分析学家们引进无限过程的权利,那些批评家就注定要失败。倘若遇到像一个连续而又无处可微的函数这种直觉上的困难,那么学者们理应修正他们的直觉,而不是抛弃他们面前的数学。分析学的严格性因为柯西而提高,又因为魏尔斯特拉斯而达一个新的顶峰。无论人们是否喜欢它,逆转终归是不可能的。
在持续不断的起伏中,数学家们建立起雄伟的理论体系,然后寻找足以揭示他们的思想界限的恰当反例。这种理论与反例的对照成为正确推理的引擎,凭借这种工具,数学得以进步。因为我们唯有知道某些特性是如何丧失的,方能了解它们是怎样发挥作用的。同样,我们唯有认清直觉是如何把人引入歧途的,方能如实地评价推理的威力。