维托·沃尔泰拉（1860—1940）

在19世纪后半叶意大利出现的一批并驾齐驱的数学家中，维托·沃尔泰拉是久负盛名的佼佼者。同他的同胞朱佩塞·佩亚诺（1858—1932）、犹金尼奥·贝尔特拉米（1835—1900）和尤里斯·迪尼（1845—1918）一样，由于在像静电学和流体力学这样的应用科学领域以及像数学分析这样的理论研究领域作出了贡献，他在科学史上留下不可磨灭的痕迹。自然，我们在这里要考察的是他的后面一种贡献。

虽然沃尔泰拉出生在亚德里亚海之滨，但是他是在意大利中部的佛罗伦萨长大的，这座城市是意大利文艺复兴运动的发祥地。在佛罗伦萨，沃尔泰拉徜徉于伟大艺术家米开朗琪罗漫步过的街道，就读于以诗人但丁和科学家伽利略命名的学校。15世纪和16世纪佛罗伦萨文艺复兴时代的气息仿佛渗入了他的骨髓，因为沃尔泰拉酷爱艺术、文学和音乐，正如他热爱科学一样。他俨然是一位博学多才的文艺复兴式的人物，虽然那场开始于佛罗伦萨的运动已经过去了三个世纪。

除这些事业外，他的政治勇气也是值得称赞的。沃尔泰拉目睹了法西斯头目墨索里尼在20世纪20年代的发迹和上台，他站在公开反对的立场，并在一份抵抗这个政权的声明上签名。这个举动最终使他丢掉了工作，然而这让他成为意大利那个时代知识界中的一位英雄。直到1940年他去世时，意大利尚未摆脱法西斯统治的灾难，但是沃尔泰拉已经为预期中的美好前景进行了奋勇战斗。

如果说晚年时代的沃尔泰拉展现出了巨大勇气，那么少年时代的他则显示了绝顶的聪慧。年幼的沃尔泰拉早在11岁时就阅读了大学水平的数学教科书，给他青春时期的教师们留下深刻的印象，并且还在高中时已通过某种途径在佛罗伦萨大学谋求得物理学实验助理的职位。他在学术上的发展突飞猛进，并在22岁时所写的物理学博士论文中达到顶峰。1

1 这段传略是根据Dictionary of Scientific Biography（《科学家传记词典》）vol. XIV, pp. 85-87的“沃尔泰拉”条目编写的。

在这一章我们要讨论沃尔泰拉的两项早期发现，两者都是在1881年发表的，这是他在高中毕业三年之后。第一项发现是找到一个病态函数，在不断增加的病态函数反例表中又增添了一个新的实例，并且从这个例子找到黎曼积分中以往从未引起人们注意的一个漏洞。第二项发现看似矛盾而实际是正确的，就是获得对于病态函数具有其自身限度的证明，因为沃尔泰拉证明了这样一个定理：不可能存在在每个有理数点连续而在每个无理数点不连续的函数。这样一种函数由于过度病态而无法存在。我们将要全面考查这个定理，不过先从那个病态函数的反例的简要说明开始。

沃尔泰拉病态函数

我们在第6章曾见过微积分基本定理的第二种形式，由柯西陈述如下：

“如果函数F是可微的，并且它的导数F'是连续的，那么。”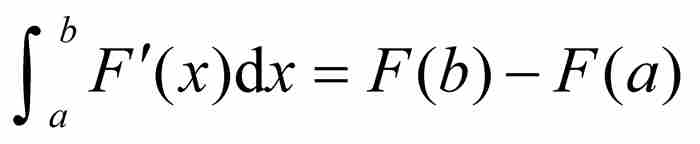

不严格地说，这表明在正确条件下导数的积分恢复其原函数。柯西在定理的证明中利用了两个假设：（a）函数F存在导数，（b）这个导数自身是连续的。但是，这两个假设是必要的吗？

假设（a）似乎是不可或缺的，因为我们不能指望在导数不存在的情形下对一个导数进行积分。然而，假设（b）的必要性就值得怀疑了。为了使基本定理成立，难道我们必须作出像F?的连续性这样严格的限制吗？

这并不是一个无足轻重的问题。我们在第10章曾见过，不能把导数的连续性视为理所当然的事情，因为函数

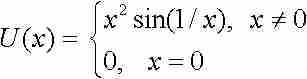
就有一个不连续的导数。另一方面，我们无需用导数的连续性作为一个积分存在的保证，因为很容易找到导数不连续然而却是可积的函数。

于是，问题在于，如果说存在任何条件的话，那么我们应该对导数F'加上什么条件方能保证基本定理成立。过去的种种发现为数学家们提供一种看待这个问题的视角，而这是柯西不曾有过的，所以看来值得重新讨论这个重要的定理。

在1875年，伽斯腾 · 达布成功地削弱了假定（b）。他证明，只要（a）函数F是可微的，以及（b'）它的导数F'是黎曼可积的，就有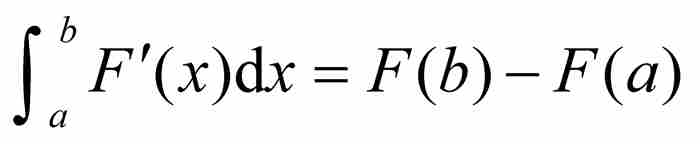。因此，为了保证基本定理成立，我们不再需要假定F'的连续性，只要求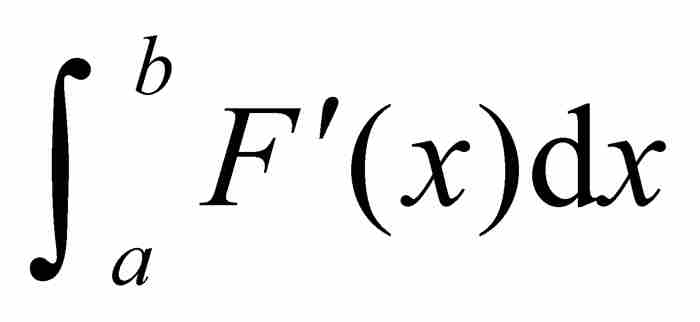存在就足够了。

这已经算是一种进展，但是依然存在一个关于F'的问题，即我们是否需要对它作出不同于存在性的其他任何假设。或许导数是可积的原系它们固有的特定性质。要是如此，我们就可以同时抛弃假定（b）和（b'），并且单独在假定（a）的基础上建立微积分的基本定理。那样将是一种限制更少和更显优雅的情况。

这就特化成这样一个问题：可能允许导数带有何等不良特性？在第10章我们证明了达布定理，那里纵然不要求导数是连续的，但是它必须具备介值特性。在那一点上，导数似乎是完全“顺从的”，而数学家们可能猜测这样的顺从性将包含可积性。

年轻的沃尔泰拉在他1881年发表的论文“论积分学原理”2中驳斥的正是这个错误概念。在那篇论文中他提供了一个函数F的例子，F在所有点具有有界的导数，但是它的导数是极端不连续的，以致是不可积的。换句话说，尽管F是处处可微的，而且它的导数F'也是有界的，然而积分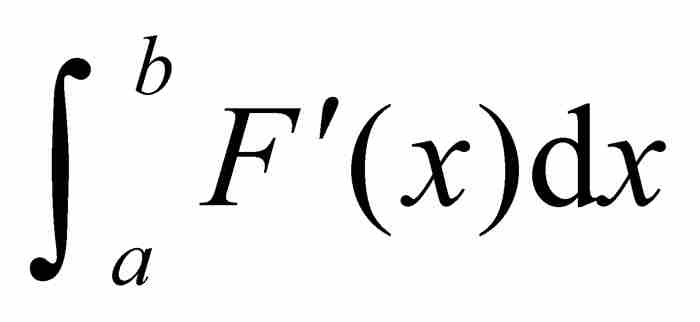并不存在。正是由于这个原因，等式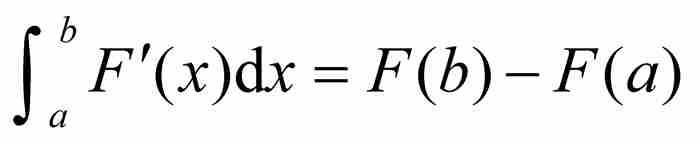不再成立。沃尔泰拉的例子之所以引人注目，不是因为这个式子的左端同右端不等，而是因为左端的积分是没有意义的。

1 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, pp. 16-48。

对于他的病态函数例子我们不作仔细考察，一部分原因在于这个函数很复杂，而另一部分原因是只在一章中讨论一个病态函数（魏尔斯特拉斯病态函数）或许就足够了。有兴趣的读者从文献3中会找到对于沃尔泰拉的工作的讨论。

2 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 56-57。

有一件事是明确的：黎曼积分的另一个不祥特征已经被揭露。数学家们喜欢的无非是一个简洁的定理，大意是如果F是可微的，并且具有有界的导数F'，那么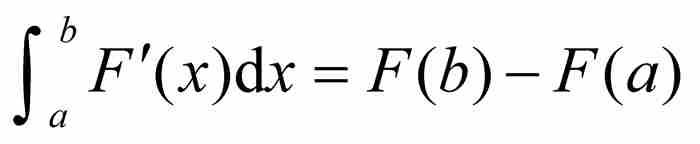。但是，沃尔泰拉证明了，就黎曼积分而论这个定理是不成立的。

对于沃尔泰拉的奇特例子，数学家们可以作出何种反应？一种选择是接受这个结果，然后继续前进。当应用这个定理时，简单地附加一个关于导数F'的额外假设。这将是阻力最小的途径。

不过，还有另外一种选择。正如我们先前所见，黎曼积分不能保证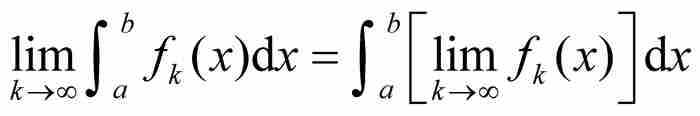。如今，沃尔泰拉已经使建立一个简单的微积分基本定理的任何希望化为泡影。在19世纪临近终结之际，有着比以往更多的理由怀疑，麻烦隐藏在黎曼积分的定义中而不在分析学的固有本性中。少数大胆的人，为了挽救上述基本定理，在沃尔泰拉病态函数的推动下打算放弃黎曼积分。不过我不再继续讨论。

汉克尔的函数分类

截至19世纪80年代，分析学受到病态函数反例的巨大冲击，这些反例看起来一个比一个奇特。我们已经见过的反例包括以下三个。

（a）狄利克雷函数

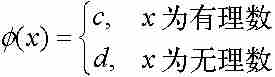
它是处处不连续的但不是黎曼可积的函数。

（b）扩充的直尺函数R(x)，它是在每个无理数点连续而在每个有理数点不连续的函数，但是它是黎曼可积的，其积分。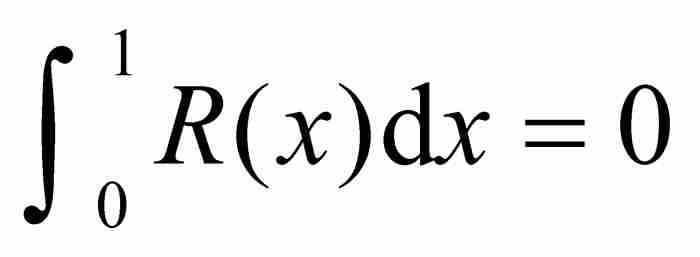

（c）魏尔斯特拉斯病态函数

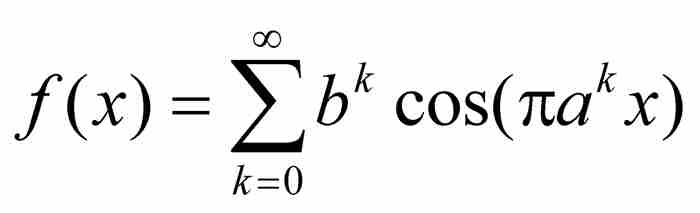
它是处处连续的和无处可微的函数。

这种情景显示分析学中存在的混乱局面，而且唤起对于如此杂乱无章的数学现状确立秩序和条理性。

竭力完成这个重任的人正好是赫尔曼·汉克尔（1839—1873）。他是黎曼的仰慕者，黎曼相信应该像生物学家或者地质学家那样，采用某种类似的方法对函数进行分类。汉克尔于1870年（早逝之前三年）提出了这样一种分类。他希望用这种分类阐明数学分析的性质和限度。

汉克尔考察由定义在一个区间[a, b]上的所有有界函数构成的函数族，并且通过它们的连续性和不连续性的性质对它们加以区分。为了了解他是如何进行分类的，我们回顾格奥尔格·康托尔曾经给出的一个熟悉的定义。

定义　对于一个实数集A，如果在任何开区间中至少包含A的一个元素，就说A是稠密的。

稠密集的两个基本例子是有理数集和无理数集，因为任何一个开区间都含有无限多有理数和无理数。稠密集这个名称带有启示性，表明它的元素如此紧密地聚集在一起，以致它们总是毗连的。

有了这个准备，我们就可以对函数给出汉克尔的分类。他把在区间[a, b]上的所有点连续的函数列为第1类函数。这些函数具备很好的特性，它们在区间上达到极大值和极小值，具有介值特性，并且能够积分。在汉克尔的分类中，第1类函数处于“食物链”的顶端。

他的第2类函数包括那些在[a, b]上除有限个点之外是连续的函数。这类函数带有更多的不确定性，但是它们的奇异性在数量上是有限的，在很大程度上处于控制之中。一个例子是我们在第10章见过的定义在区间[-1, 1]上的函数

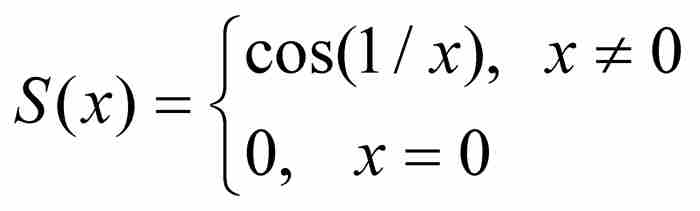
因为它在x = 0有一个不连续点。换一种方法，我们还可以取一个在区间[a, b]上定义的连续函数，然后，例如在50个点上把它重新定义成不连续的，由此引入50个不连续性点。这样一个函数将属于汉克尔第2类函数。

从逻辑上说，只剩下一类函数了，即那些在[a, b]上具有无限个不连续点的函数。自然，这些函数是最差的，但是汉克尔相信可以把它们再分成差的和非常差的两类：

3A类：在[a, b]的无穷个点不连续但是仍然在其中一个稠密集上连续的函数。他把这类函数称为“点态不连续的函数”。

3B类：一切其他的不连续函数。汉克尔称之为“完全不连续的函数”。

我们看出，3A类函数中的一个点态不连续函数，尽管存在无限多个不连续点，但是仍然在任何开区间的某些地方是连续的。另一方面，对于3B类中的一个函数而言，必定存在区间（a, b）内的某个开子区间（c, d），函数在其中完全没有连续的点。因此，一个完全不连续的函数的特征是在一个不间断的子区间上仅存在不连续的点。

试问，前面引入的三个病态函数属于汉克尔分类方案中的哪一类？狄利克雷函数是处处不连续的函数，属于完全不连续的3B类函数。直尺函数在无穷个点（有理数点）是不连续的，然而在一个稠密集（无理数点）上是连续的，因此属于点态不连续的3A类函数。魏尔斯特拉斯函数或许是最为奇特的，把它归入第1类函数看似不当而实则正确的，因为它是处处连续的。

汉克尔发现，他的函数分类在下述意义下是重要的：他知道了第1类函数和第2类函数是黎曼可积的，并且他了如指掌的那些点态不连续函数的例子同样是可积的。相反，完全不连续的狄利克雷函数是不可积的。对于他而言，3A类函数同3B类函数之间的鸿沟似乎是不可跨越的。正如Thomas Hawkins指出的那样，“汉克尔通过确定点态不连续函数同完全不连续函数之间的区别，相信自己已经把数学分析可以处理的函数同那些它无力处理的函数分离开来”。1

1 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, p. 30。

为了显示这样做的全部价值，汉克尔证明了一个惊人的定理：区间[a, b]上的一个有界函数是黎曼可积的，当且仅当它不比点态不连续函数更差。这就是说，一个有界函数只要属于第1类、第2类或者3A类函数，那么它是可以积分的；那些属于3B类的函数是不可以积分的，而且也不能进行解析开拓。

汉克尔定理看起来是在回答我们前面提出的主要问题：一个可积函数可能在多大程度上是不连续的？按照他的说法，答案是“在最坏的情况下是点态不连续的”。他的证明表示，只要一个函数在一个稠密集上是连续的，所有那些不连续的点对于可积性而言都是无足轻重的。这恰好是数学家们梦寐以求的简洁结果。

不幸的是，这也是不正确的。

在这种错综复杂的概念中，即使大学问家也难免犯错误，不过汉克尔所犯的是一个突出的错误。公正地说，他的定理有一半是正确的：一个函数如果是黎曼可积的，那么它确实必定在一个稠密集合上是连续的。一个完全不连续的函数存在一个由不连续点构成的不间断的子区间，它不可能具有黎曼积分。关于这一点，人们再次想到狄利克雷函数。

但是，汉克尔对于相反结论的证明存在漏洞。英国数学家亨利·约翰·斯蒂芬·史密斯（1826—1883）发表了一个点态不连续的函数的例子，而这个函数却是不可积的。他指出：“这个函数是值得注意的，因为它同一种不连续函数的理论对立，而这种理论得到卓越的几何学家赫尔曼 · 汉克尔博士的首肯，他在不久前英年早逝是数学科学的巨大损失。” 2 史密斯的例子是非同寻常的，其中用到一种我们如今称为具有正测度的无处稠密集的结构。需要了解细节的读者，请参阅Thomas Hawkins的著作。3 暂时，我们仅限于指出，函数的连续性同黎曼可积性之间的关系依然是不清楚的，仍旧没有解决一个可积函数可能在多大程度上是不连续的问题。无论点态不连续性的价值怎样，它都不能对于人们长期以来寻找的这种联系提供答案。

2 H. J. S. Smith, “On the Integration of Discontinuous Functions”, Proceedings of the London Mathematical Society, vol. 6 (1875), p. 149。

3 Thomas Hawkins, Lebesque's Theory of Integration, Chelsea, 1975, pp. 37-40。

不过，已经取得了一定进展。黎曼已经把可积性概念扩展到某些高度不连续的函数，而汉克尔定理正确的一半以及史密斯的函数反例，证明了黎曼可积函数完全包容在一个更大的函数集合内，即由在稠密集上的连续函数组成的集合。

我们顺便指出，“点态不连续的”这个术语有时被粗心大意地用来表示“在最坏的情况下是点态不连续的”。就是说，凡是属于汉克尔的第1类、第2类或3A类中的所有函数都被归并在点态不连续函数这个单一的标题下，这就导致把连续函数（第1类函数）置于“点态不连续函数”之列这种离奇的局面。由于前面三类函数的一个共同特性是在稠密集上是连续的，我们可以把稠密地连续的看成是概括第1类、第2类和3A类中所有函数的术语。

无论如何，初看起来汉克尔的函数分类似乎是一个大有可为的工具，能够把分析学可以处理的函数同分析学难以对付的函数分离开来。然而，结果却是许多难以对付的函数在集合论和勒贝格积分的范围内得到非常巧妙的处理。如今，汉克尔的函数分类多半被束之高阁。

但是在19世纪后期，点态不连续性仍然是最出色的数学家们研究的对象。21岁的维托·沃尔泰拉就是这些数学家中的一位。

病态函数的限度

病态函数的盛行显示，函数的任何特性，无论它多么稀奇古怪，通过一位极富创造性的数学家精心构造出的例子，都是可以被认识的。

例如，谁能想象直尺函数竟然会在每个无理数点连续而在每个有理数点不连续呢？此外，为什么不假定在某处存在一个有待发现的同样离奇的函数，这个函数在每个有理数点连续而在每个无理数点不连续？似乎并不是一个例子比另外一个例子更加怪异。

从下面的两个例子中，明显看出函数的连续性点同不连续性点有时是可以交换的。首先定义函数

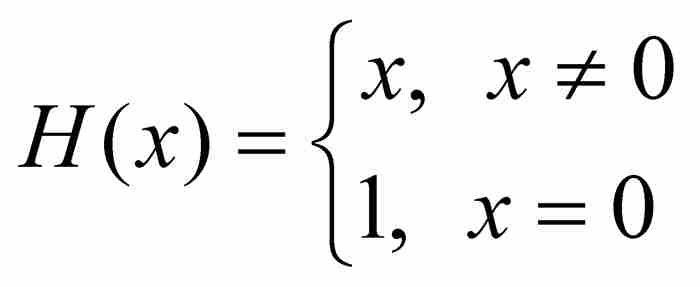
显然这是在除原点以外的所有点连续的函数，原点是其唯一的不连续点。

作为H(x)的相似函数，我们引入

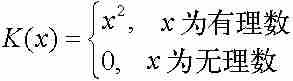
不难看出，K(x)在任何点a = 0是不连续的。因为如果令{x_k}是一个收敛于a的有理数序列，而{y_k}是一个收敛于a的无理数序列，那么

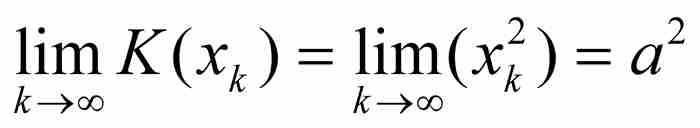
然而

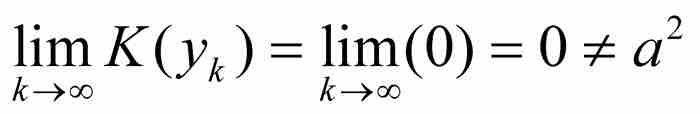
由于这两个序列具有不同的极限，我们知道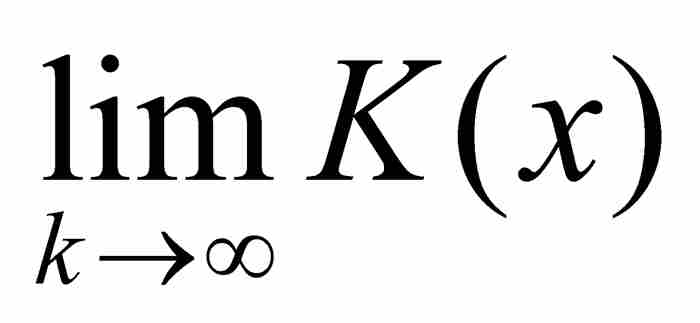不可能存在，所以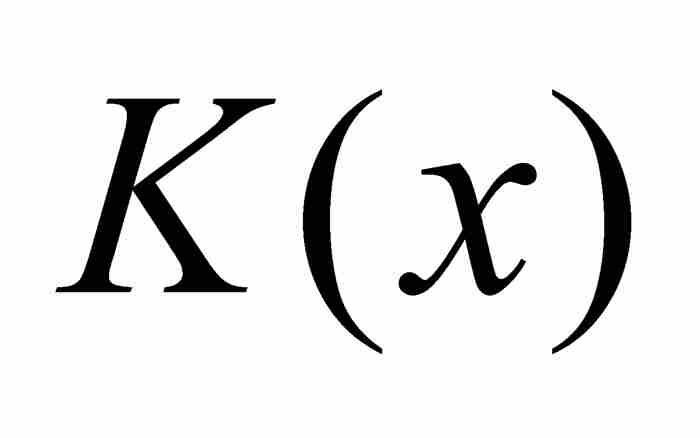在x = a是不连续的。

但是，对于任何x，不管它是有理数还是无理数，我们都有 0≤K(x)≤x2，所以用简单的挤压论证，证明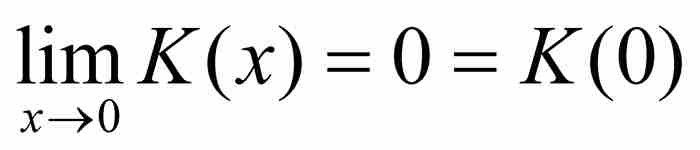。由此推出K有唯一的连续点，即原点。所以，对于上面定义的两个函数H和K，它们连续的点同不连续的点是相互交换的。

关于这一点，我们引进下面的定义。

定义　地对于一个函数f，我们令C_f = {x| f 在x是连续的}，D_f = {x| f 在x是不连续的}。

可以把前面的讨论简单地概括为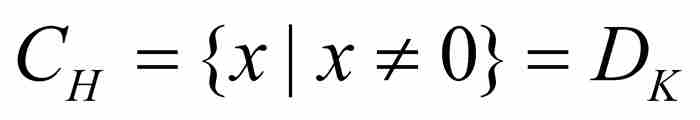和。

函数的连续性点同不连续性点的交换问题是非常有趣的。对于任何一个函数 f，是否存在一个“余函数”g满足C_f = D_g和C_g = D_f ？要是存在，我们如何把它找出来？倘若不存在，原因又在哪里？

沃尔泰拉在他1881年所写的论文“关于点态不连续函数的几点注记”中致力于解决这个问题。结果得到一个强有力的定理和两个重要推论。1

1 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 7-8。

定理　在区间（a, b）上不可能同时存在两个点态不连续函数，其中一个函数的连续性点是另一个函数的不连续性点，反之亦然。

证明　他通过反证法证明，首先假定f和φ是（a, b）上这样两个点态不连续的函数，它们的连续性点集和不连续性点集满足C_f = D_φ 和D_f = C_φ 。换句话说，C_f 和C_φ 把（a, b）划分成两个不相交的非空稠密子集。

他的证明基于一个嵌套的子区间序列。由于f是点态不连续的，它在区间（a, b）内的某处必定有一个连续的点x_{0。对于ε = 1/2，连续性保证存在一个δ > 0，使（x0 - δ , x0 + δ ）成为（a, b）的一个子集，并且只要0 < | x - x0 | < δ，就有| f (x) - f (x0)| < 1/2。现在我们选择a1 < b1，使得[a1, b1]是开集（x0 - δ, x0 + δ ）的一个闭子区间，如像图12-1中画出的那样。}

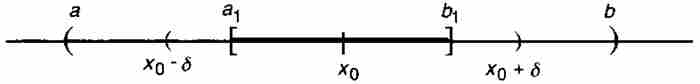
图　12-1

对于[a_{1, b1]中的任意两点x和y，应用三角不等式，得到}

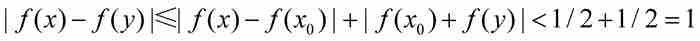（1）

这表明f在闭区间[a_{1, b1]上的振幅不超过1单位。}

但是（a_{1, b1）是（a, b）的一个开子区间，同时 φ 也是点态不连续的。因此，（a1, b1）内有φ 的一个连续点，比如说x1。重复前面对于 φ 的论证，我们找到点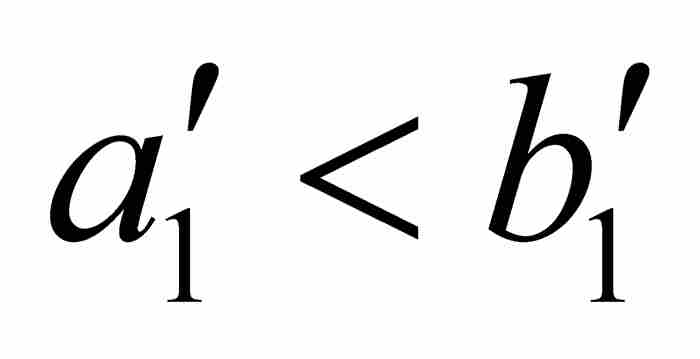，使闭区间[, 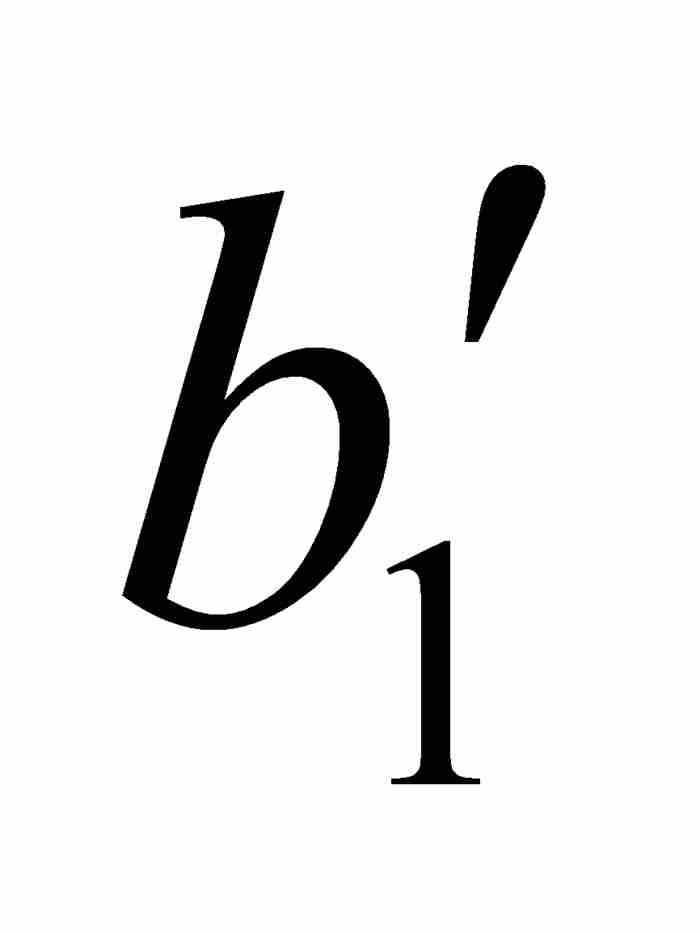]是（a1, b1）的子集，并且对于[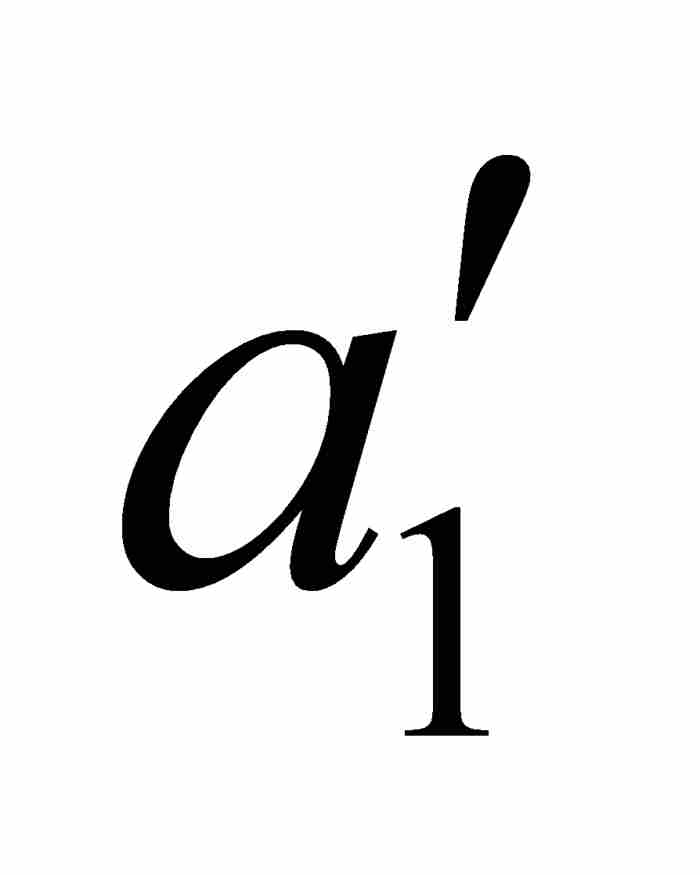, 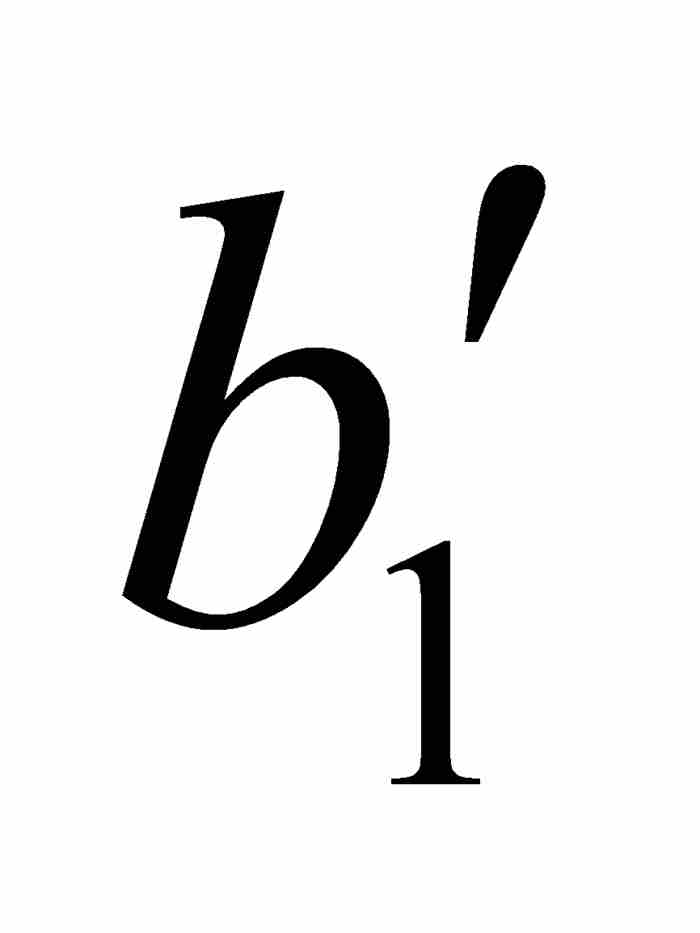]中的任意x和y有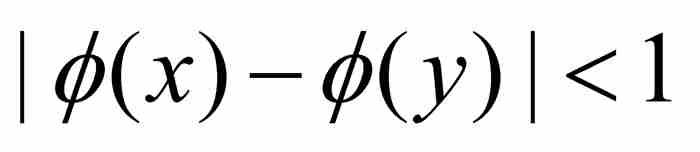。参见图12-2。}

图　12-2

把这个结论同上面的式（1）相结合，我们找到一个闭子区间[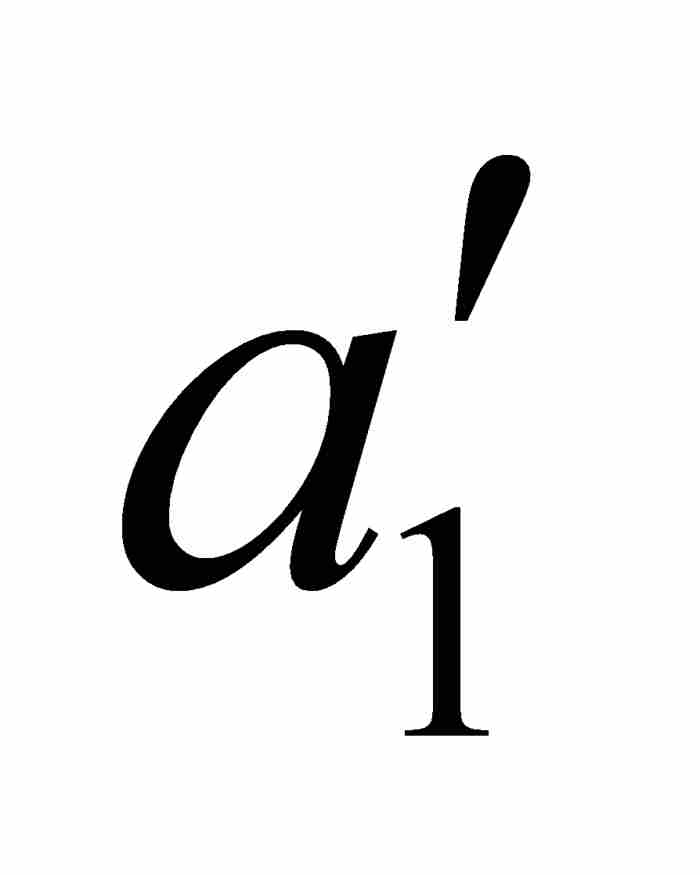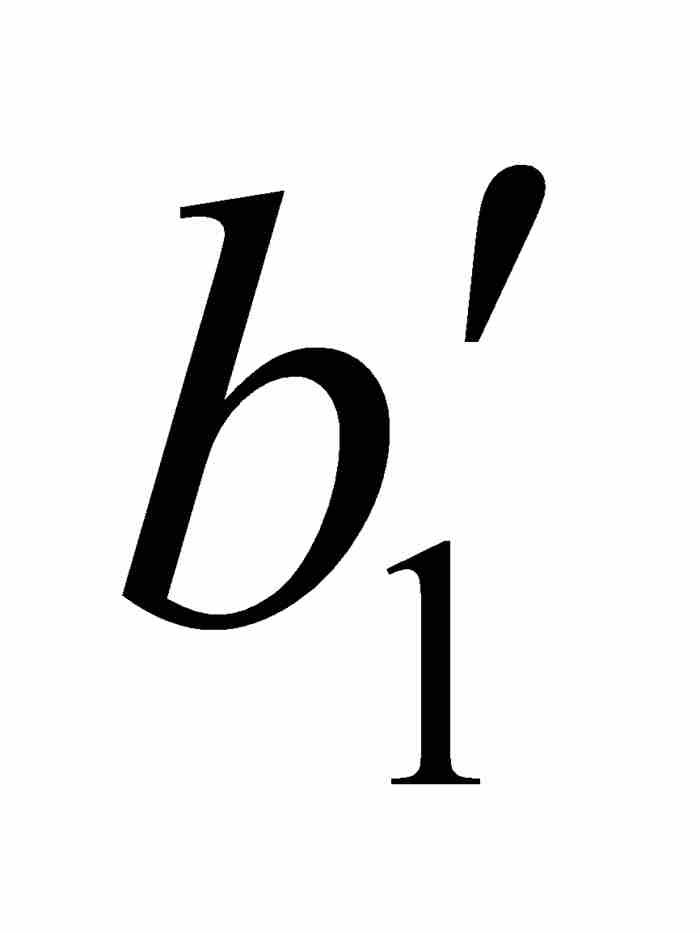，]，对于其中的所有x和y，有

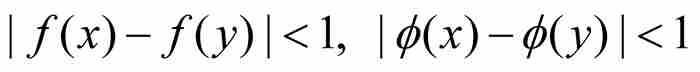
沃尔泰拉接着利用点态不连续性以 ε = 1/4重复这个论证过程。他首先考察f，然后考察 φ，找到一个位于开区间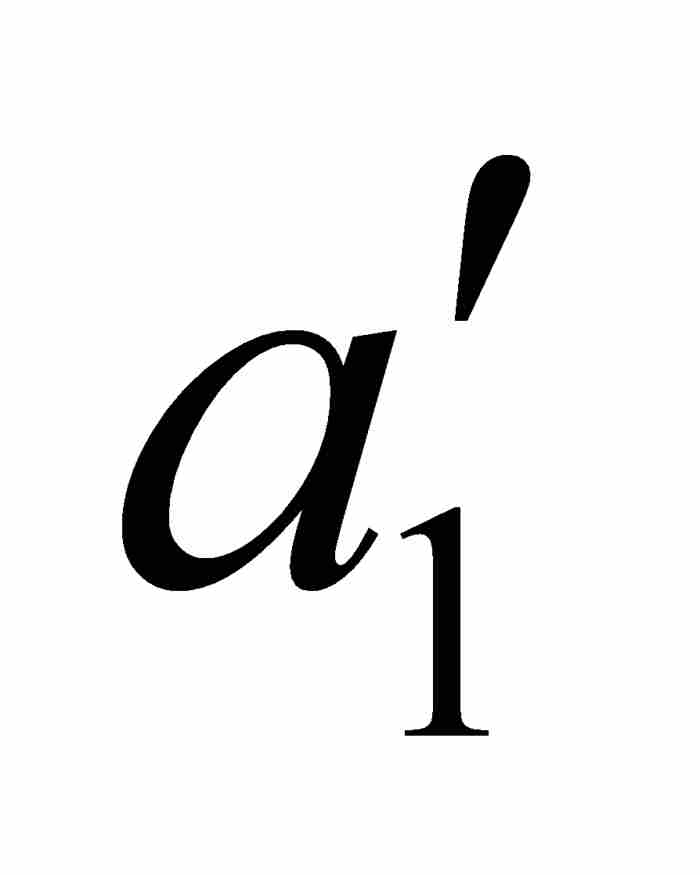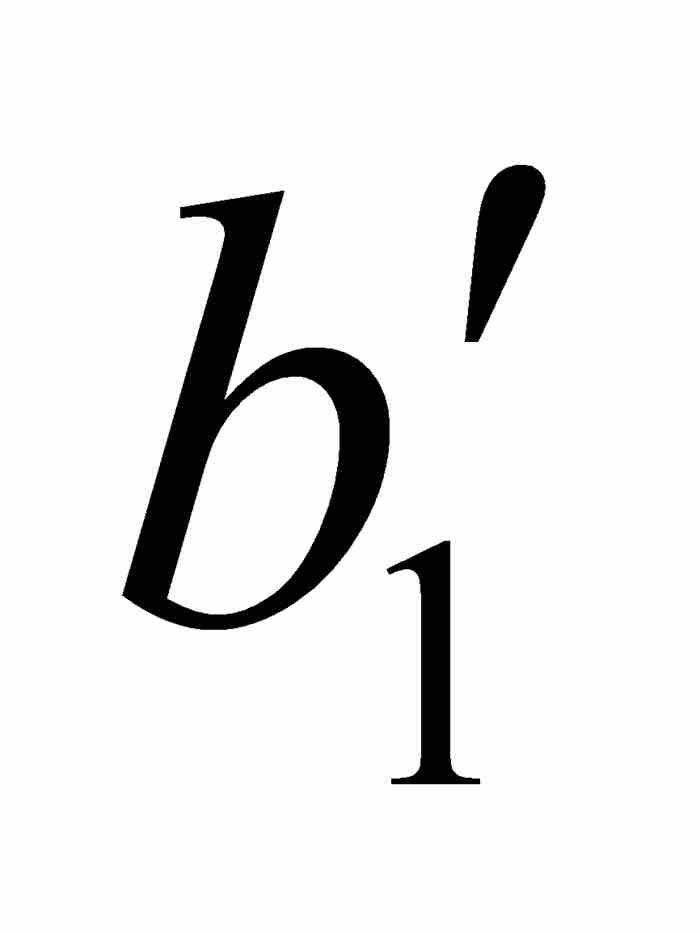（, ）内的闭子区间[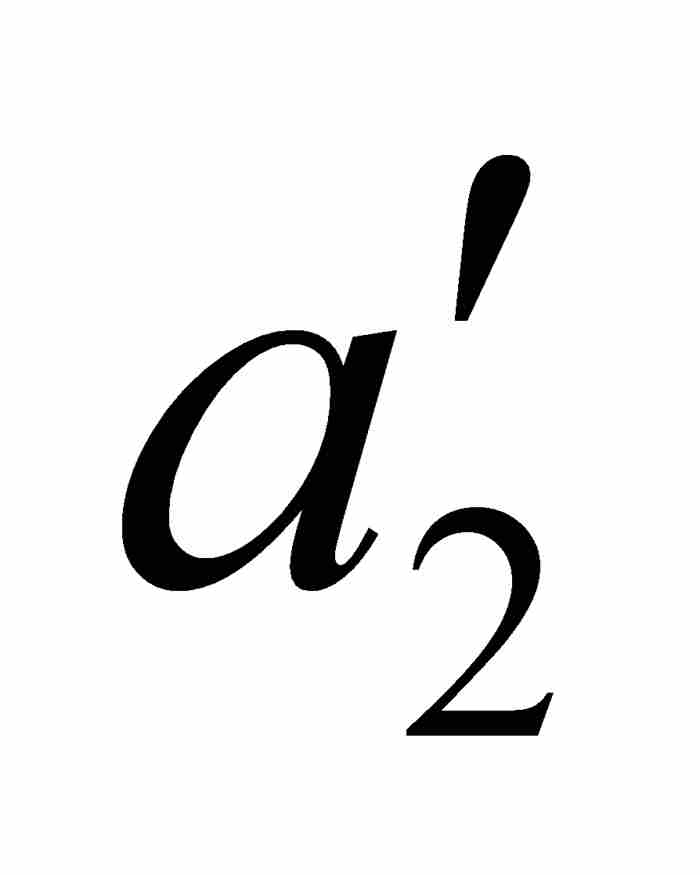, 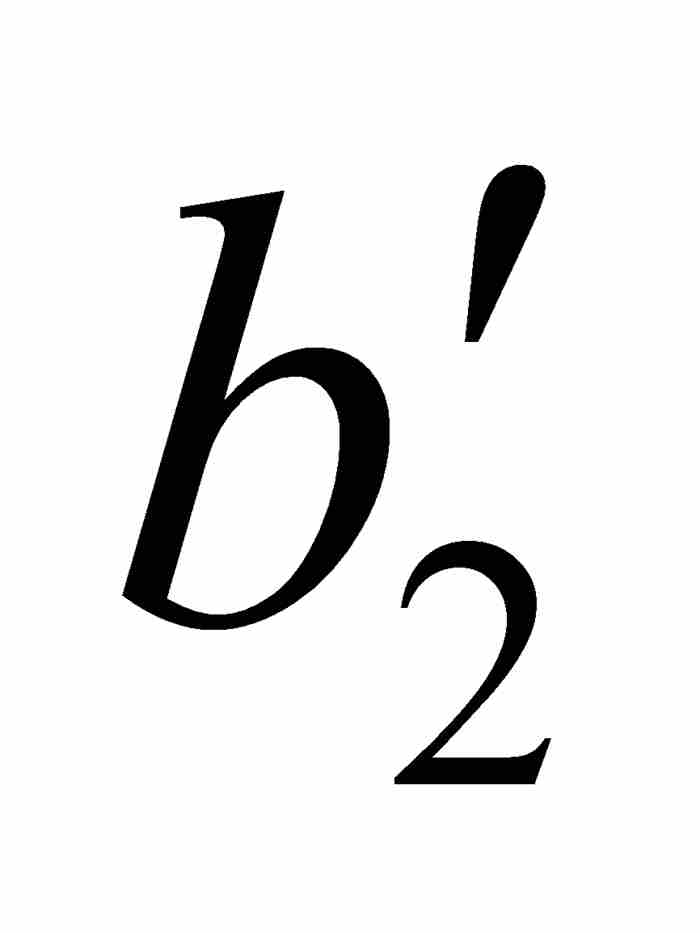]——这个闭区间自然也在[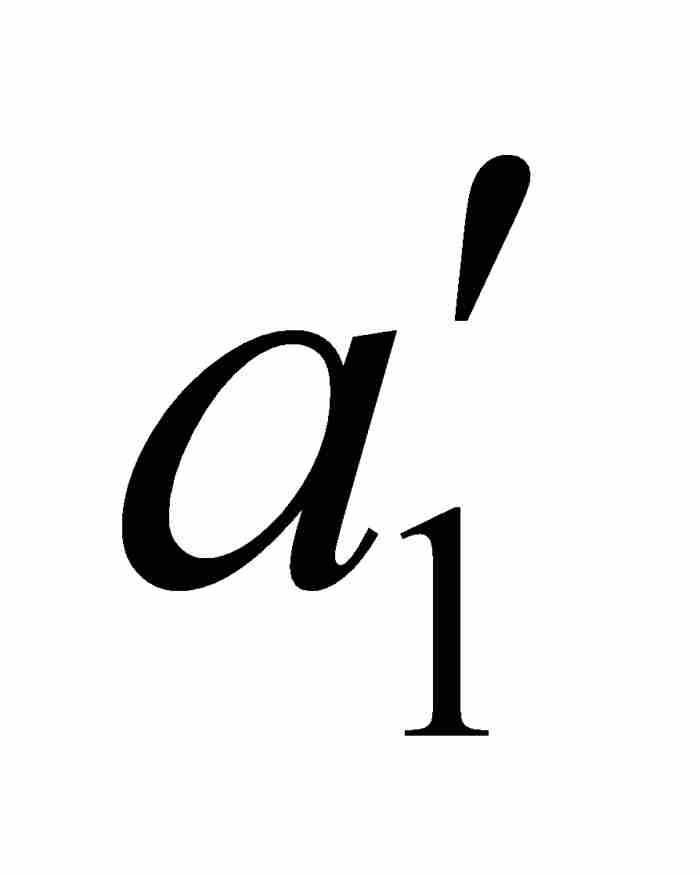, 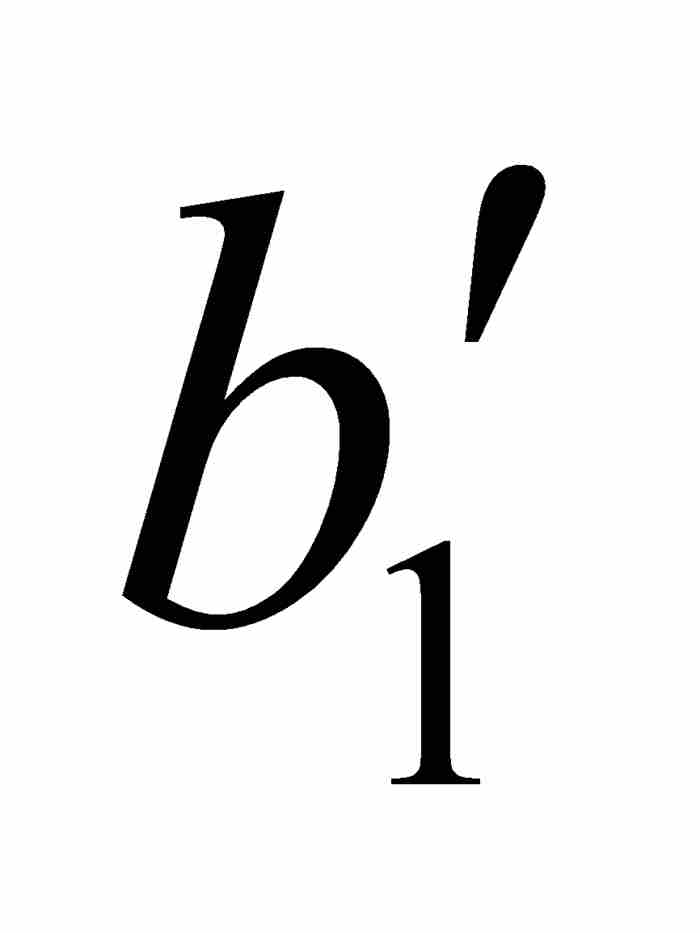]内，使得对于[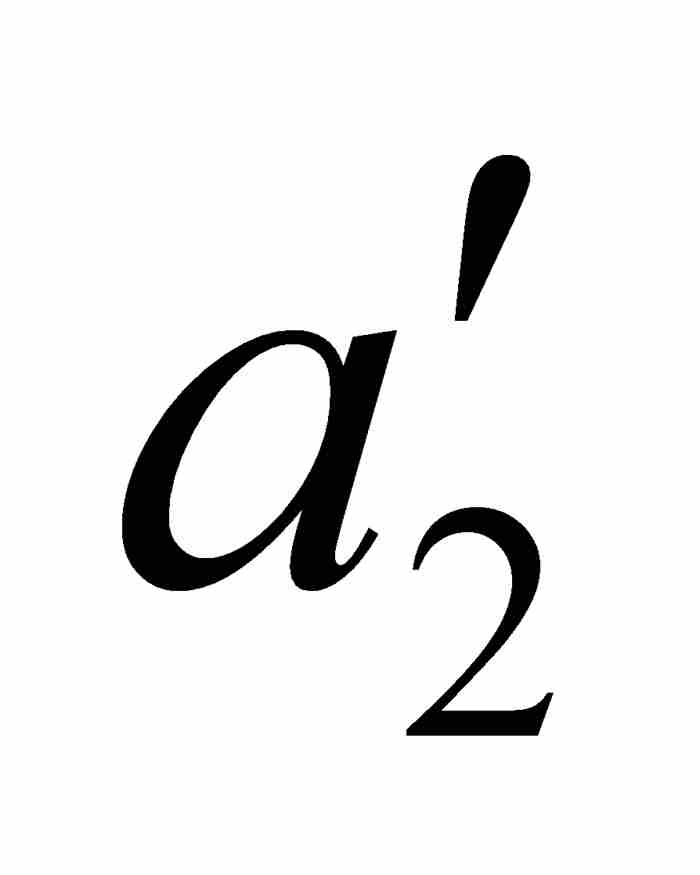, 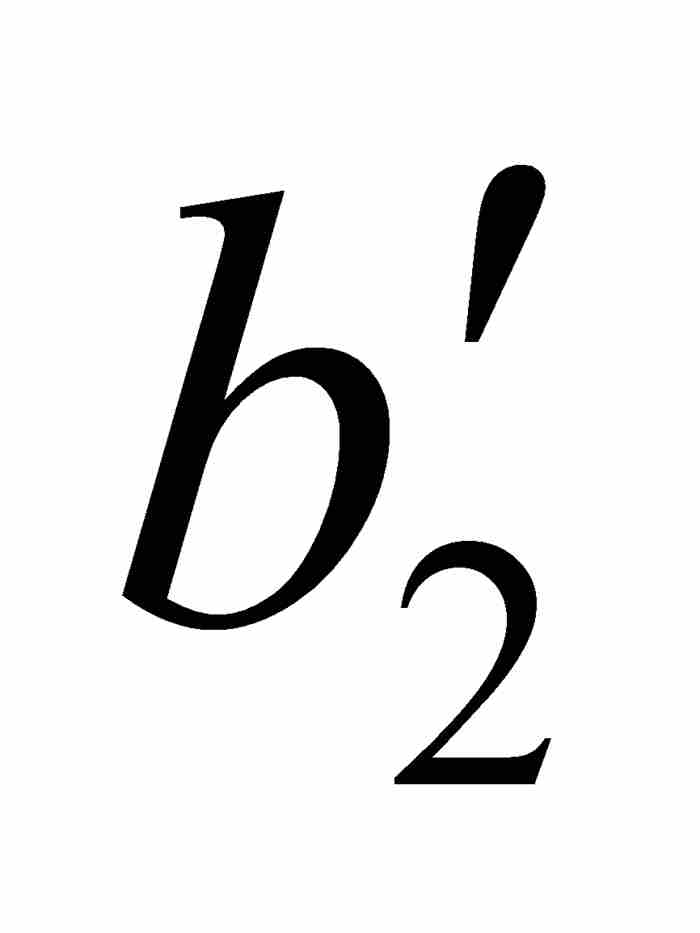]中的任何点x和y，有

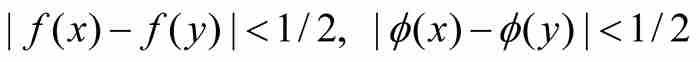
他用ε = 1/8, 1/16, …, 1/2k, …继续作下去，由此产生一个闭区间序列[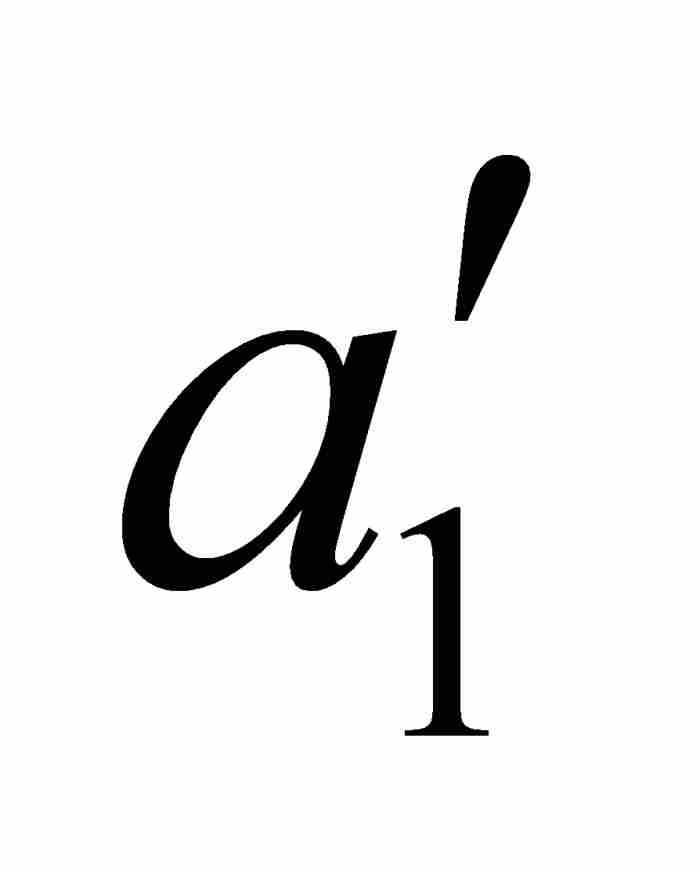, 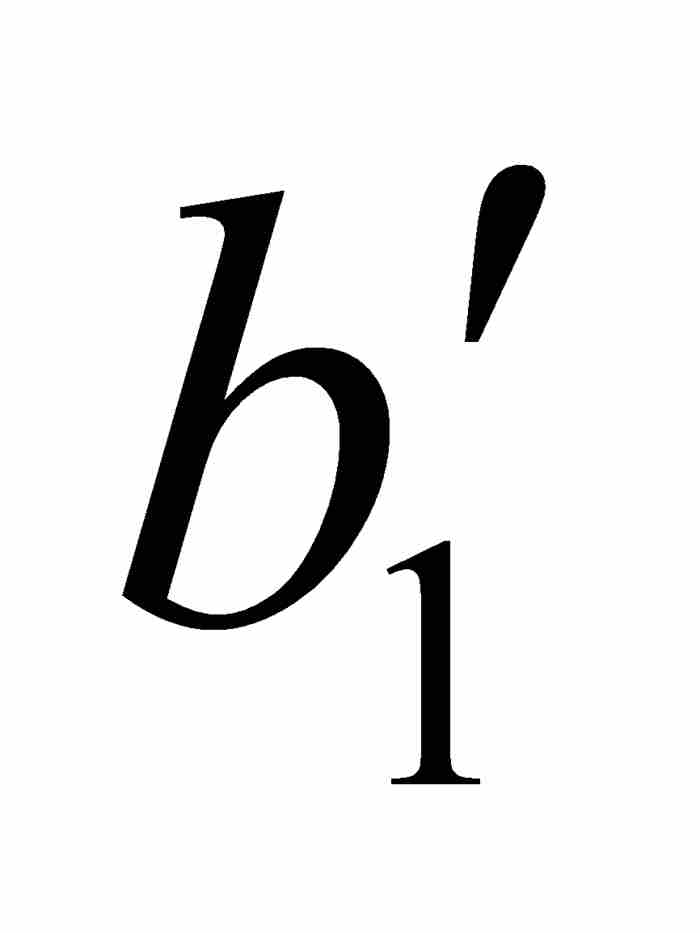] ⊃ [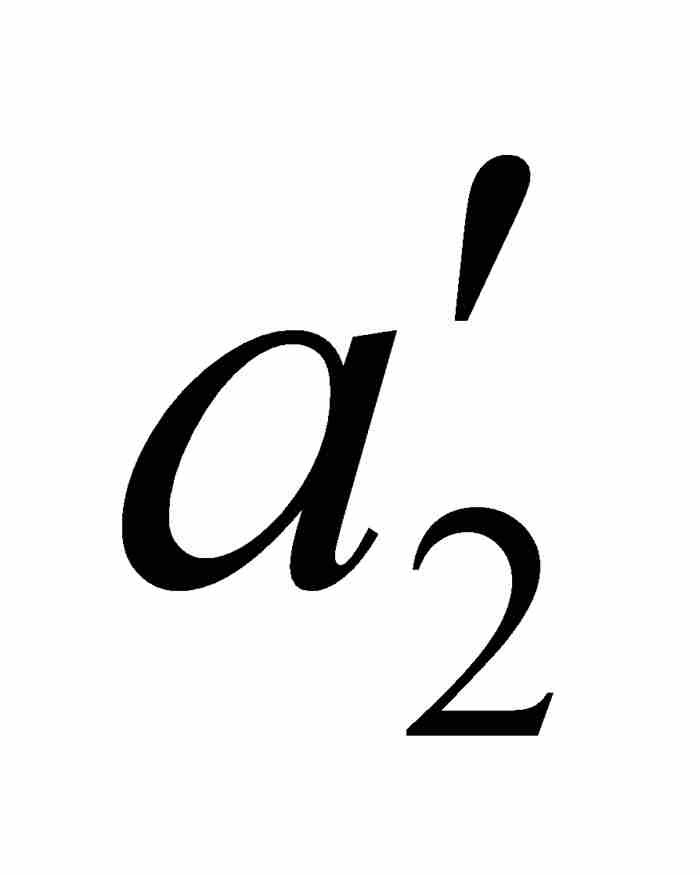, 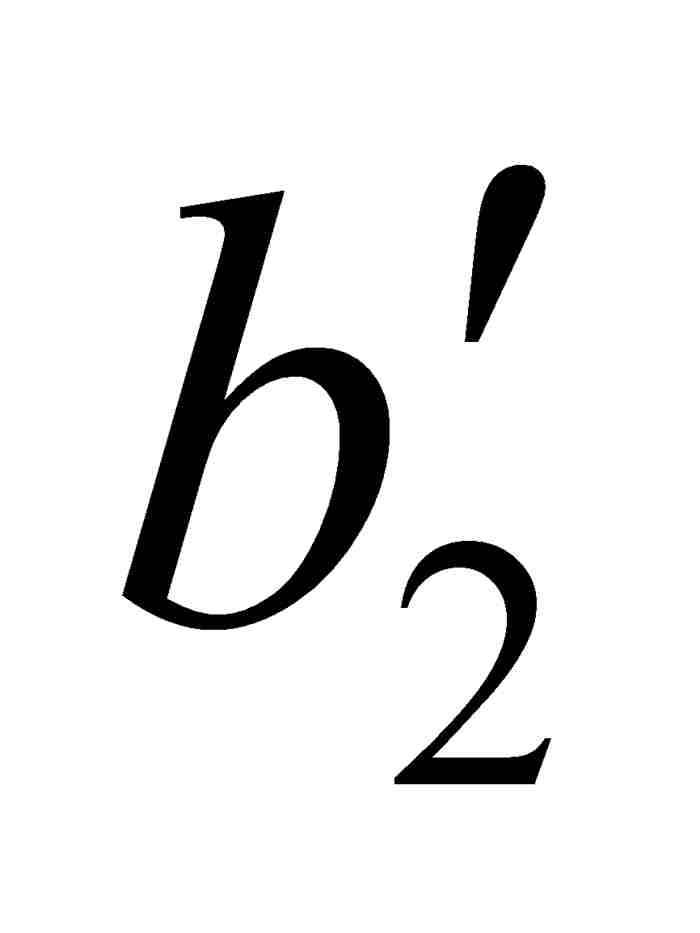] ⊃ [, 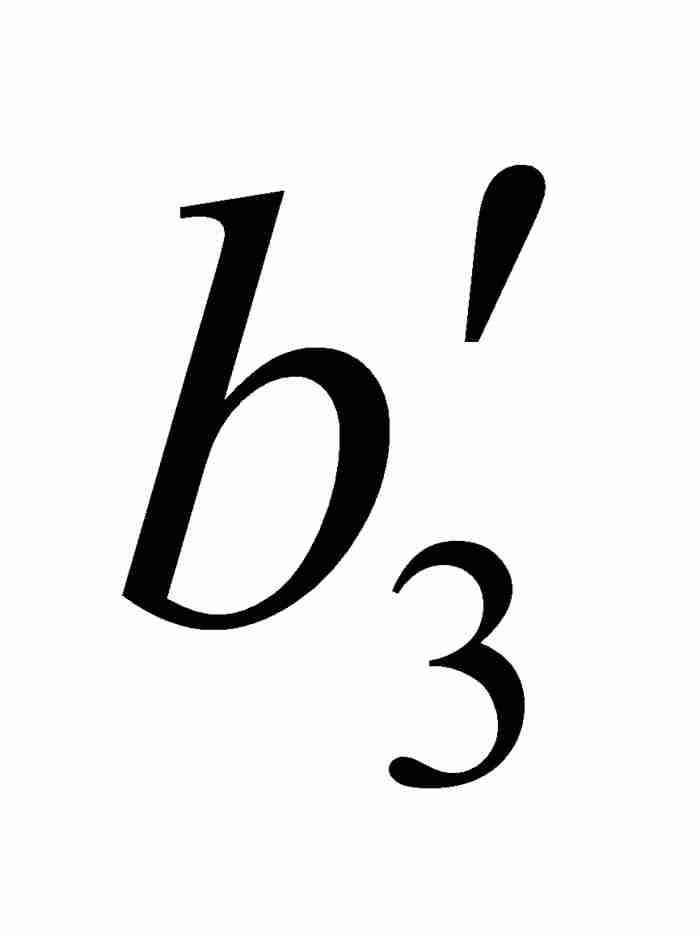] ⊃ …，使得对于[, ]中的任何点x和y，有

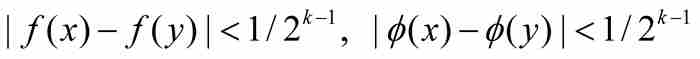（2）

一个矛盾随即发生。根据实数的完备性性质，在所有嵌套的区间[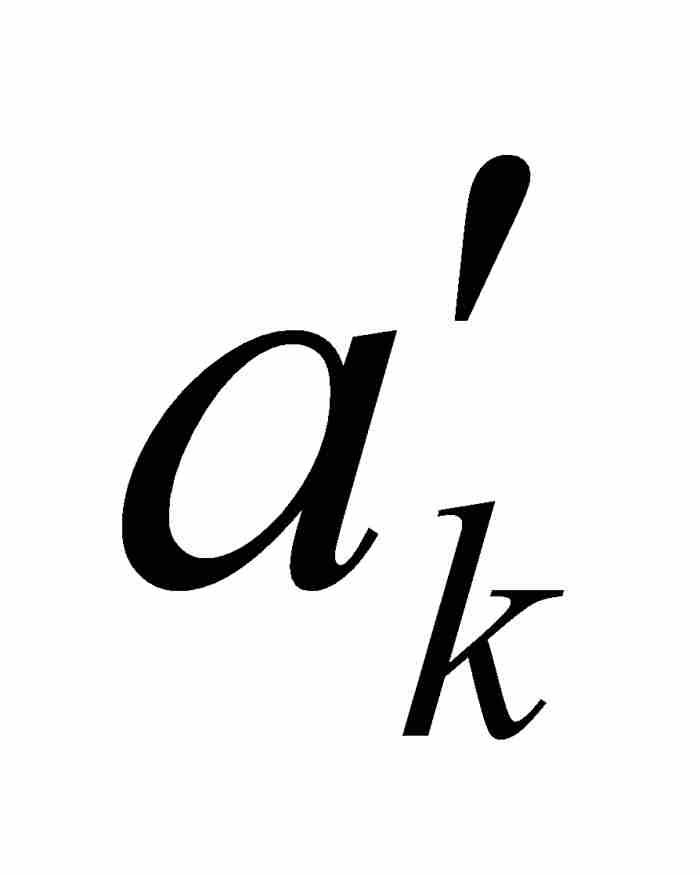, 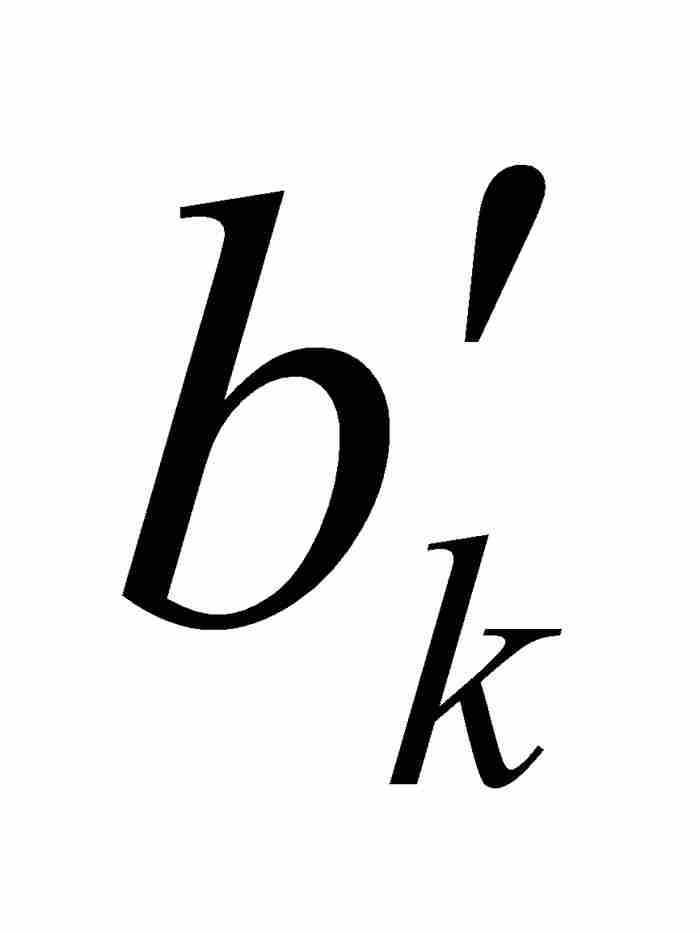]中必定存在一个公共点c。由于c位于[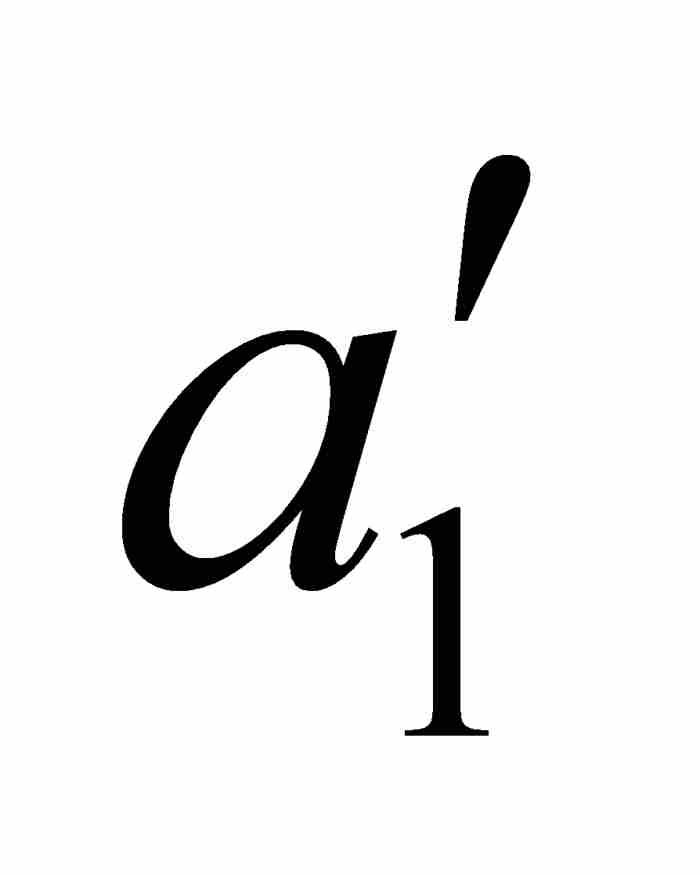, 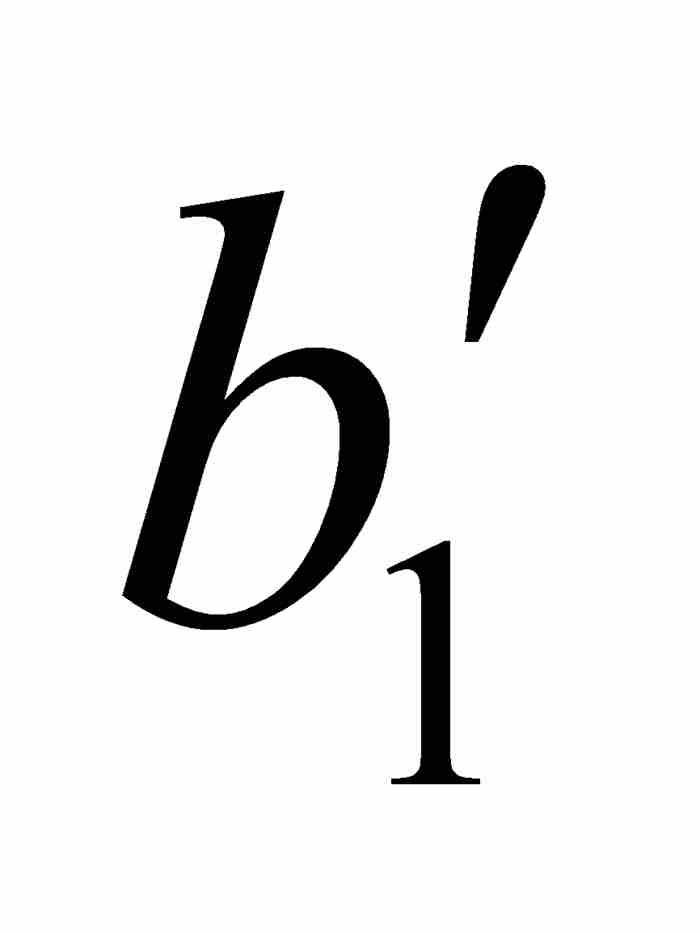]内，它实际是在我们原来的区间（a, b）内。

接下来我们断定f在c是连续的。这是很容易得出的结论，因为沃尔泰拉在构造他的嵌套的区间序列时已经控制了f的振幅。为了作出严格的魏尔斯特拉斯ε - δ 方法的证明，我们可取任意 ε > 0，并且选择一个满足1/2k-1 < ε 的自然数k。我们确知c是区间[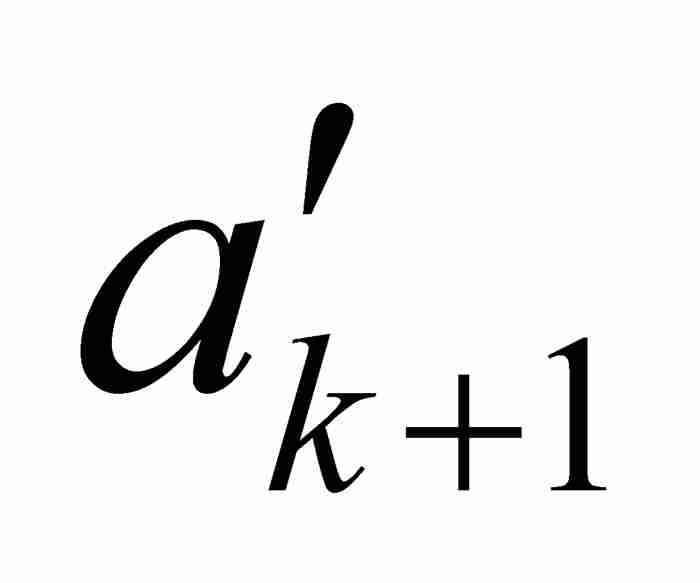, 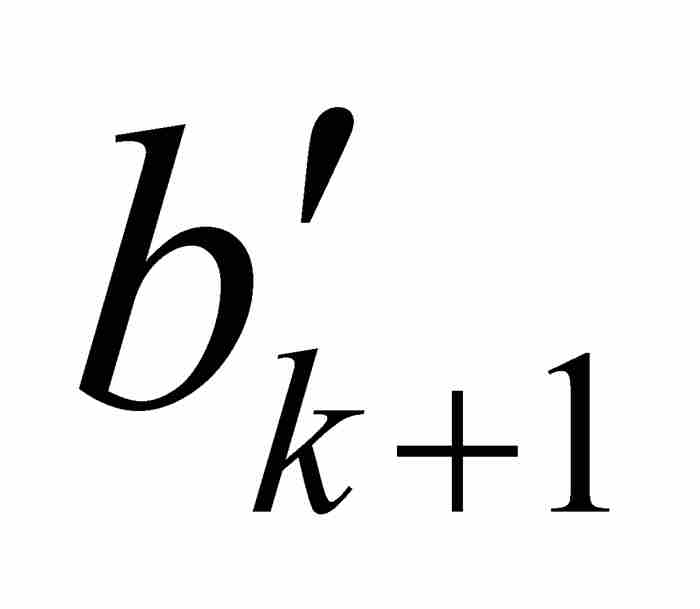]中的一点，而这个区间又是在开区间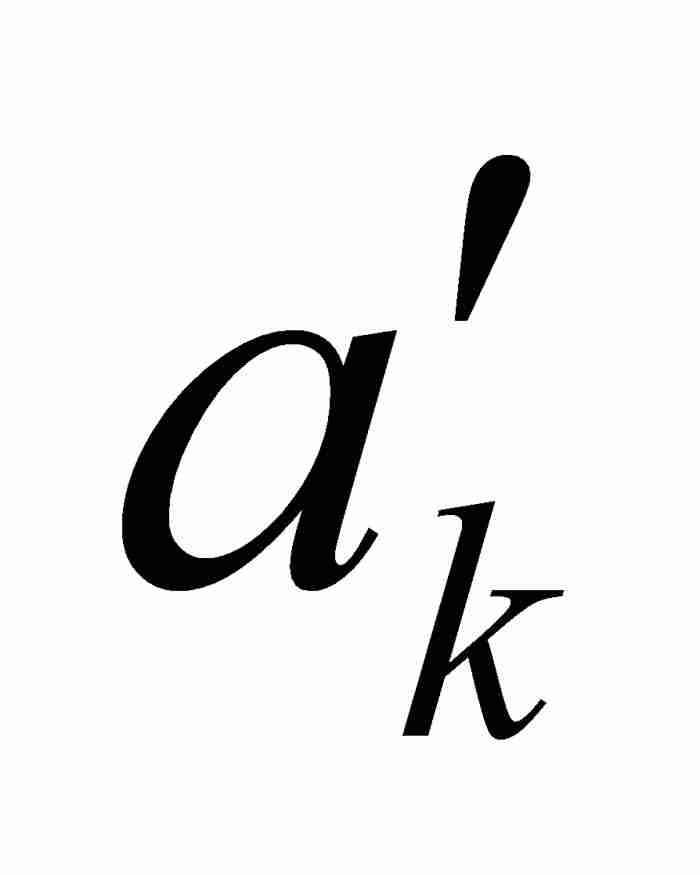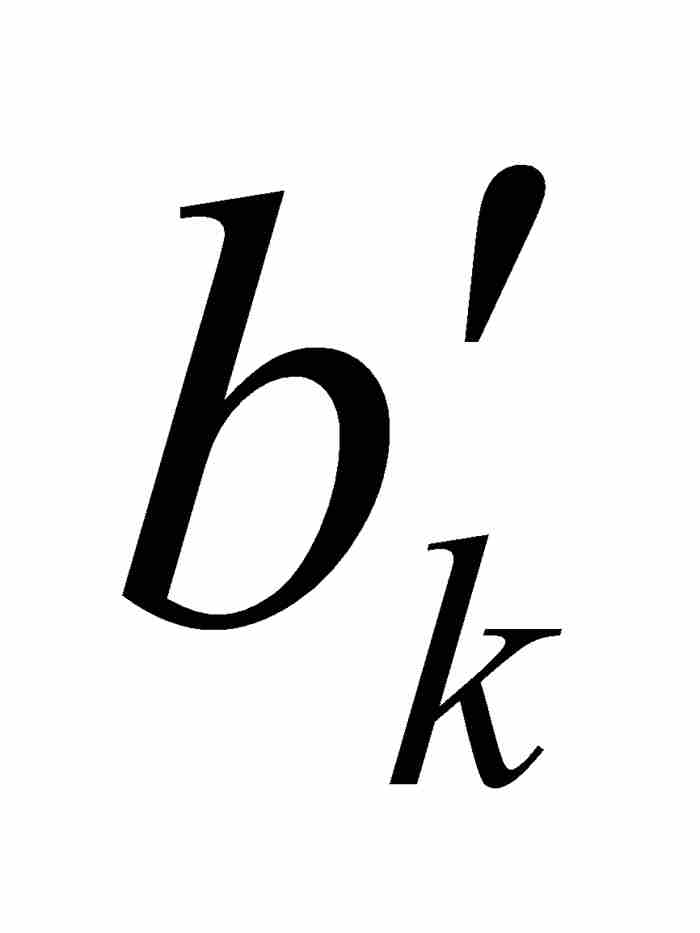（, ）内，所以可以求出一个δ > 0，使（c - δ, c + δ 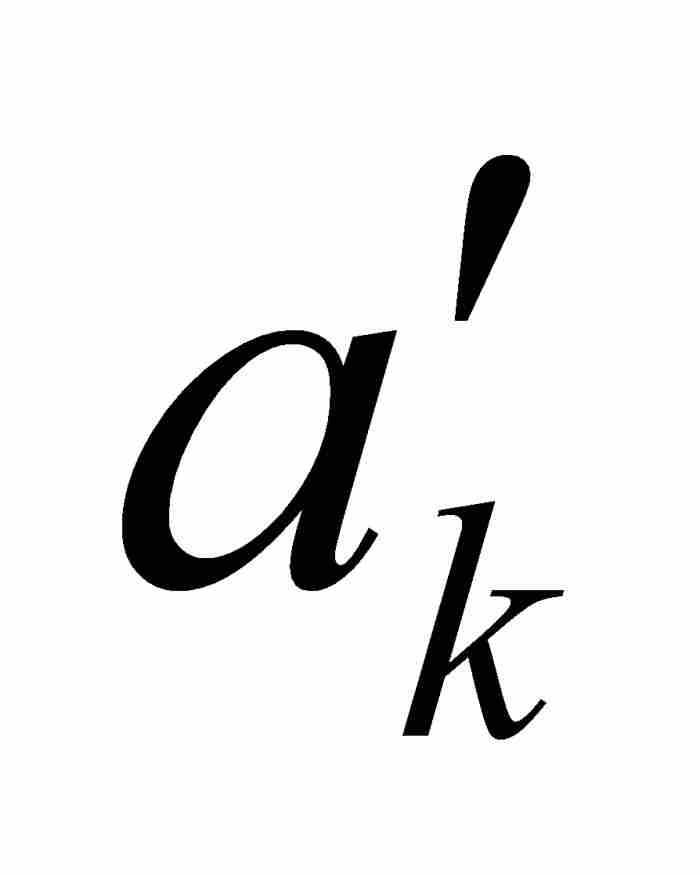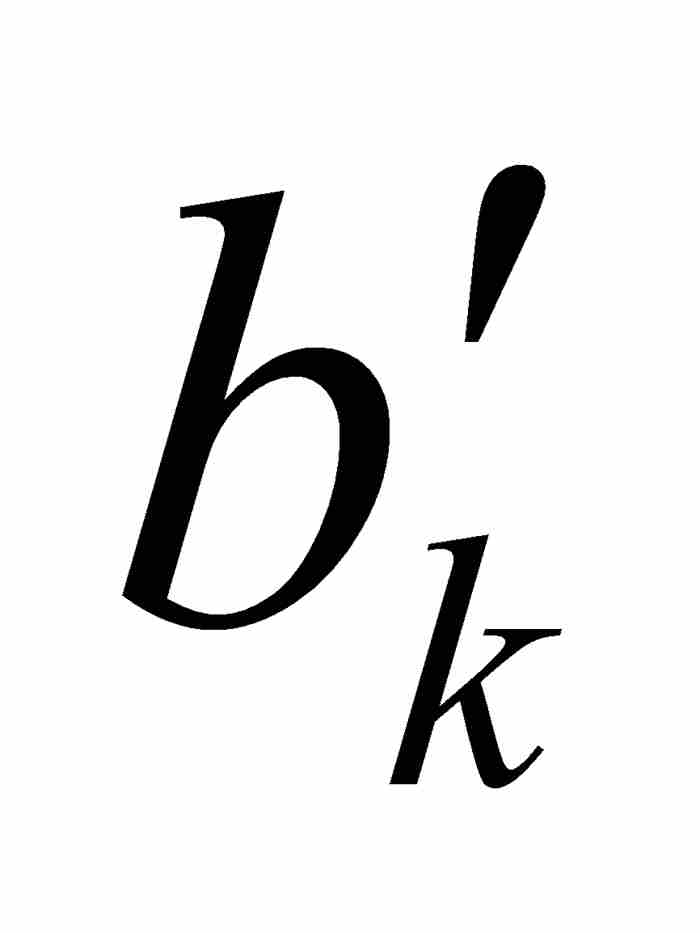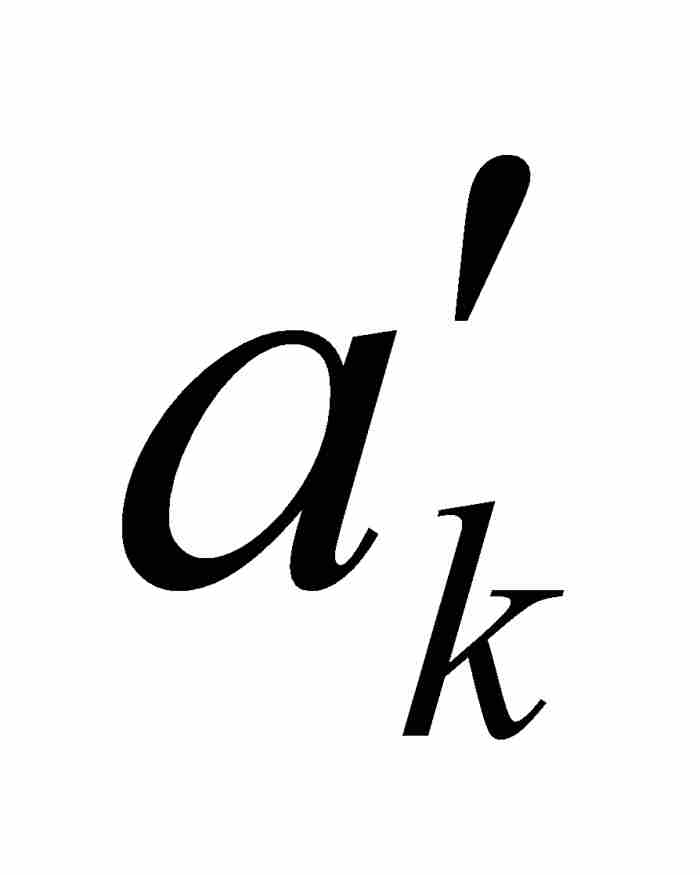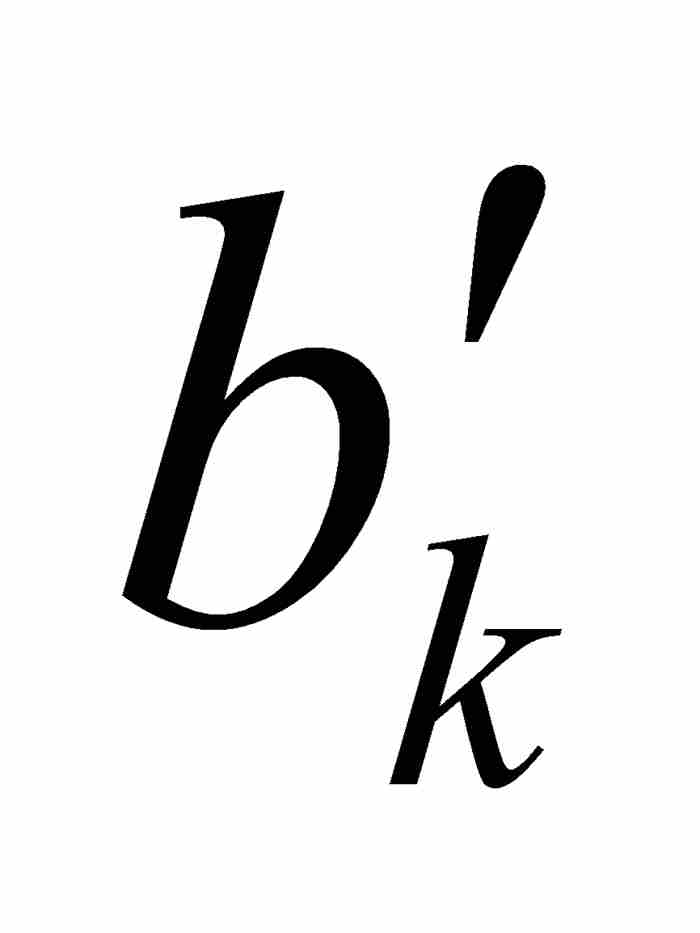）⊂（, ）⊂ [, ]。因此，对于满足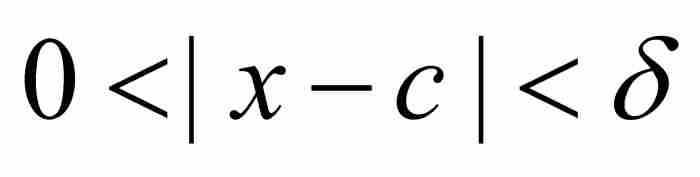的任何x，根据式（2）我们有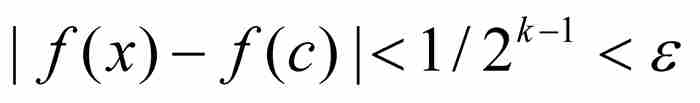。这就证明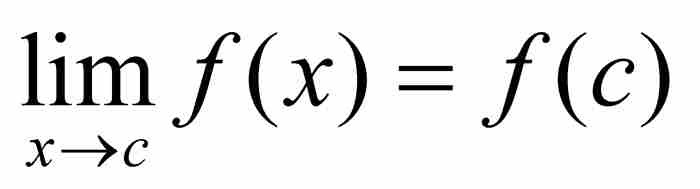，所以f在c是连续的，这正是我们要推断的结果。

由于可以把同样的论证一字不改地用于φ，所以 φ 在c也是连续的。用这种方法，我们已经引出一个矛盾，因为c同时属于C_f和C_φ，违反一个函数的连续性点是另外一个函数的非连续性点的假定。所以别无选择，我们只能断定不可能存在两个这样的点态不连续函数。

在继续讨论之前，我们需要作两点说明。首先，沃尔泰拉对于区间[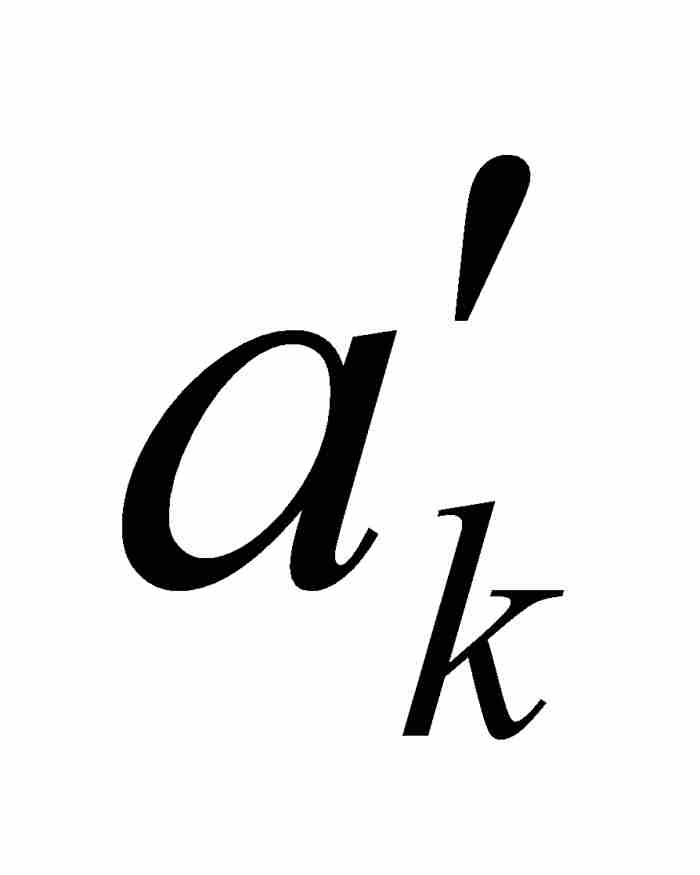, 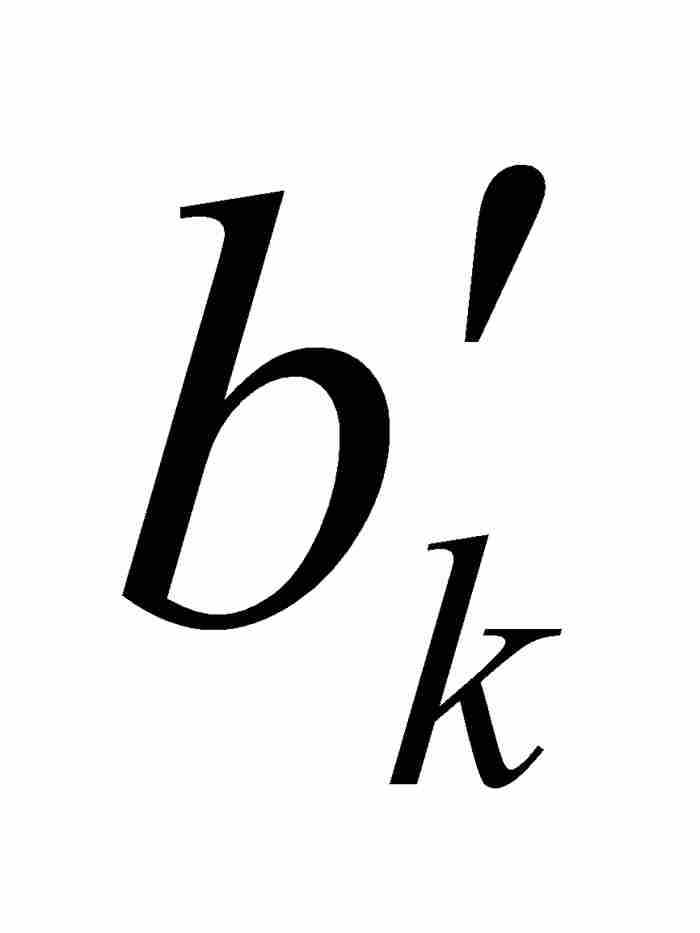]没有明确要求为闭区间。这是一个容易补救的疏忽，正如我们在上面所作的那样。其次，在前面的例子中，函数H的连续性点是函数K的非连续性点，反过来也是一样，我们注意到K是完全不连续函数（汉克尔的3B类函数）而不是点态不连续函数（汉克尔的3A类函数）。因此，那个例子同沃尔泰拉证明的结果丝毫不相抵触——恐怕任何人都会因这个结果而难以入眠。

沃尔泰拉从他的定理得出两个重要的推论。第一个推论解决了分析学中的一个主要问题，我们把它陈述如下。

推论1　由于存在一个在每个无理数点连续而在每个有理数点不连续的函数，也就不可能找到一个在每个无理数点不连续而在每个有理数点连续的函数。2

2 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 8。

为了充实他的论证的细节，我们设想这样一个函数G(x)，它的C_G是有理数集（稠密集）。那么，G是点态不连续的。但是我们已在前面遇见了扩充的直尺函数R(x)，它也是点态不连续的，其C_R却是无理数集。于是G的连续性点将是R的非连续性点，同沃尔泰拉的定理矛盾。因此，这两个函数不可能同时存在。由于直尺函数确实是存在的，所以我们不得不作出函数G不存在的结论。套用一句西部电影中对牛仔们的评论，沃尔泰拉的定理证明了“这座城市没有大到足以同时容纳他们两人”。一个函数仅在有理数点上连续从逻辑上说是不可能的。

所以，病态函数是有其限度而不是无所不包的。无论数学家们如何精明，某些函数仍然置身其外，这就是沃尔泰拉用这个巧妙的论证所证实的一个事实。但是，他还得到一个隐含的推论，那就是不可能存在无理数点上取有理数并且反过来在有理数点上取无理数的连续函数。3

3 Vito Volterra, Opere Mathematiche, vol.1, Accademia Nazionale dei Lincei, 1954, p. 9。

推论2　地不存在在实数集上定义的这样一个连续函数g(x)，当x取无理数时g(x)为有理数，而当x取有理数时g(x)为无理数。

证明　为了导致矛盾，沃尔泰拉再次假定存在这样一个函数g。然后通过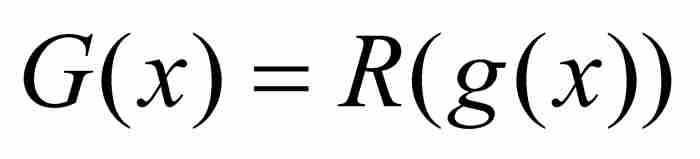，其中R是前面所说的扩充的直尺函数，并且给出关于G的两个断言。

断言1　如果x为有理数，那么G在x是连续的。

这是显而易见的，因为只要x为有理数，g(x)就是无理数，所以R在g(x)是连续的。但是假定g是处处连续的，所以复合函数G在x将是连续的。

断言2　如果y为无理数，那么G在y是不连续的。

通过选择一个收敛于y的有理数序列{x_k}，就知道这是很容易证实的。在这种情况下，

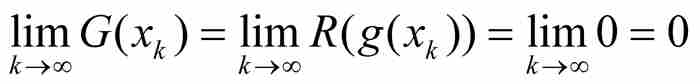
这是因为g把每个有理数x_k变换成一个无理数g(x_k)，而直尺函数R在无理数点的值为零。另一方面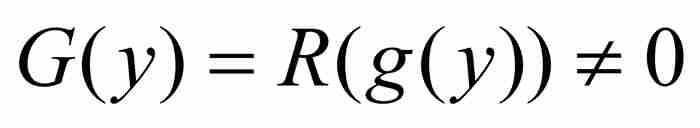，，因为g(y)为有理数。总之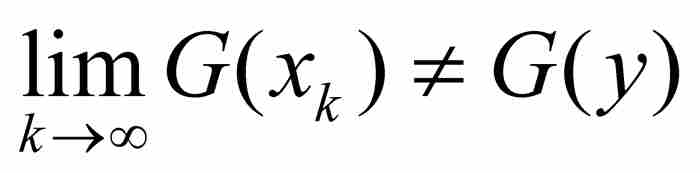，，所以G在y是不连续的。

把这两个断言结合起来，就证明了函数G在有理数点是连续的而在无理数点是不连续的——这是沃尔泰拉刚才证明不可能出现的一种局面！由此推断不可能存在像g这样的一个函数。所以，没有一个连续函数能够把有理数变换为无理数，同时反过来把无理数变换为有理数。

这些结果尤其使我们想起，虽然有理数集和无理数集都是实数的稠密集，但是它们在本质上是不可互换的。正如我们所见，康托尔曾经特别指出有理数是可数的而无理数是不可数的事实，但是事情并不止于此，数学家们还发现这两个数系之间存在某些更微妙的差别。这些差别之一是一个集合的“类型”的概念。集合的类型是由沃尔泰拉的天才学生勒内·贝尔提出的概念，他是我们在下一章介绍的数学家。

我们谨以这些叙述告别那时年仅21岁的维托·沃尔泰拉。摆在他面前的是远大而辉煌的事业，人们将会见到他继续取得数学上的成功，并得到国际上的公认，而英国国王乔治五世甚至授予他荣誉爵士称号。

追溯沃尔泰拉的后半生，我们知道他赋予19世纪以“函数论世纪”的特征。4 从欧拉最初提出函数的思想开始，函数概念在柯西、黎曼和魏尔斯特拉斯的研究中扮演主要角色，并且接着传承给新一代的康托尔、汉克尔以及沃尔泰拉本人。函数在分析学中处于至高无上的支配地位，而在函数中发现的种种意想不到的可能性，无不一次又一次地使数学家们惊诧莫名。如我们所知，由于沃尔泰拉在1881年的两项不同而又迷人的发现，使他在我们叙述的故事中占有重要的一席之地。

4 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 1023。

对于这位年轻人说来，1881年是非同寻常的一年。