典型案例

楚人有鬻盾与矛者，誉之曰：“吾盾之坚，物莫能陷也。”又誉其矛曰：“吾矛之利，于物无不陷也。”或曰：“以子之矛陷子之盾，何如？”其人弗能应也。（《韩非子·难一》）

这是韩非子所说的一个寓言故事。对此，韩非子指出：夫不可陷之盾与无不陷之矛，不可同世而立。

逻辑辨析

在上述这则寓言中，楚人违背了思维的一致性要求，前后自相矛盾。因为由“吾盾之坚，物莫能陷也”可以推出：他的盾是坚固无比的；由“吾矛之利，于物无不陷也”可以推出：他的盾不是坚固无比的。对于他的盾，楚人既断定了它是坚固无比的，又断定了它不是坚固无比的，从而得出了一对相互矛盾的判断。同样，对于他的矛，楚人既断定了它是锋利无比的，又断定了它不是锋利无比的，也得出了一对相互矛盾的判断。所以当有人问他“以子之矛陷子之盾，何如？”时，按照他前述所言，必然可以得出：他的矛既能刺穿他的盾，又不能刺穿他的盾。因此他便陷入了进退维谷的两难之境。

知识链接

思维的一致性要求我们在同一思维过程中，对于同一个思想不能既肯定它又否定它。保持思维的一致性，要求做到两个方面：

一、概念要相容

就概念而言，思维的一致性要求在同一时间、同一地点对同一对象是否具有某一属性要有一致的断定。在同一个概念中，一个对象不能既具有某一属性，又不具有某一属性。一个概念如果违反了这一要求，则称之为“矛盾概念”，如“不能用十三个字来表达的概念”、“圆的方”等都是矛盾概念。

二、判断要一致

就判断而言，思维的一致性要求我们在同一思维过程中，不能既断定某对象是什么，又断定它不是什么。

违反思维的一致性要求就会陷入“自相矛盾”。例如：

（1）一个小村庄的理发师宣称：只给那些不给自己理发的人理发。

（2）好好先生雇了甲、乙两个园丁帮助自己管理菜地。在除草时，园丁甲发现一只蜗牛正在吃雇主的卷心菜，于是准备处死它，园丁乙急忙制止他，两个人为之争执起来。好好先生听到争吵声，走过来询问究竟。园丁甲说：“这只蜗牛在吃您的卷心菜，所以，得处死它。”好好先生说：“你说的对！”园丁乙说：“蜗牛也是一个生命啊，所以，不能处死它。”好好先生说：“你说的对！”他的夫人听到了，说：“可是他们两个人说的不可能都对啊！”好好先生说：“你说的也对！”

（3）历山之农者侵畔，舜往耕焉，期年，甽亩正。河滨之渔者争坻，舜往渔焉，期年而让长。东夷之陶者器苦窳，舜往陶焉，期年而器牢。仲尼叹曰：“耕、渔与陶，非舜官也，而舜往为之者，所以救败也。舜其信仁乎！乃躬藉处苦而民从之。故曰：圣人之德化乎！”

或问儒者曰：“方此时也，尧安在？”

其人曰：“尧为天子。”

“然则仲尼之圣尧奈何！圣人明察在上位，将使天下无奸也。今耕渔不争，陶器不窳，舜又何德而化？舜之救败也，则是尧有失也。贤舜，则去尧之明察；圣尧，则去舜之德化：不可两得也。”（《韩非子·难一》）

在上例（1）中，小村理发师的宣称看似合理，实质包含矛盾。按照他的宣称，他该不该给自己理发呢？如果他不给自己理发，则他属于不给自己理发的人，根据他的宣称，那么他该给自己理发；如果他给自己理发，则他属于给自己理发的人，根据他的宣称，那么他又不该给自己理发。这样，根据他的宣称，他既该给自己理发，又不该给自己理发，从而犯了“自相矛盾”的错误。在上例（2）中，在对于蜗牛的实际行动上，要么处死它，要么不处死它。如果按甲的做法是要处死它，乙的做法是不要处死它，好好先生同时肯定这两者：既处死它又不处死它，这违反了矛盾律。他夫人认为应该是：他们两人说的不可能都对，即“处死它”、“不处死它”不可能都对。好好先生又加以肯定，这等于同时肯定“既处死它又不处死它”与“不可能‘既处死它又不处死它’”，而这又是一对矛盾，好好先生又再次违反了矛盾律。因此，好好先生好好地犯了一次“自相矛盾”的错误。在上例（3）中，韩非子指出，“贤舜”与“圣尧”是一对矛盾，儒者们的观点实际上是犯了“自相矛盾”的逻辑错误。

扩展延伸

正因为我们要保持思维的一致性，所以，如果从一个判断推出了一对相互矛盾的判断，那么该判断是不能接受的。在这方面，有两个最常见的应用，就是反证法和归谬法。反证法是说，如果我们要证明一个判断成立，就要先假定这个判断不成立，由此推出矛盾，从而得出原判断成立。归谬法是说，如果我们要证明一个判断不成立，就要先假定这个判断成立，由此推出矛盾，从而得出原判断不成立。不过，在一般情况下对反证法和归谬法不加区分。请看下面的两道题：

（1）《高中数学·选修2—2》（人教版）中有这样一道题：

证明质数有无穷多个。

证明：假定质数不是有无穷多个，而只有有限多个。设全体质数为p_{1，p2，p3，…，pn。令p=p1p2p3…pn+1。}

显然，p不含质因数p_{1，p2，p3，…，pn。p要么是质数，要么含有除p1，p2，p3，…，pn之外的质因数。这表明，除质数p1，p2，p3，…，pn之外，还有质数。因此，假设不成立。于是，质数有无穷多个。}

（2）《高中物理·必修1》（人教版）中有这样一道题：

亚里士多德认为物体下落的快慢是由它们的重量决定的。伽利略认为这是不正确的，他的证明如下：

根据亚里士多德的论断，一块大石头的下落速度要比一块小石头的下落速度大。假定大石头的下落速度为8，小石头的下落速度为4，当我们把两块石头捆在一起时，大石头会被小石头拖着而减慢，结果整个系统的下落速度应该小于8；但是两块石头捆在一起，总的重量比大石头还要重，因此整个系统下落的速度要比8还大。这样，就从“重物比轻物落得快”的前提推断出了互相矛盾的结论，这使亚里士多德的理论陷入了困境。为了摆脱这种困境，伽利略认为只有一种可能性：重物与轻物应该下落得同样快。

上例（1）中的证明使用的就是反证法，例（2）中伽利略的证明使用的就是归谬法。

勤思多练

1.试分析下列论述中是否存在违反思维一致性的情况。

（1）一位年轻人去见爱迪生，他满怀信心地对爱迪生说：“我想发明一种万能溶液，它可以溶解一切物品。”爱迪生听罢惊奇地说：“那么你想用什么器皿放置这种溶液呢？”年轻人哑口无言。

（2）公输盘为楚造云梯之械，成，将以攻宋。子墨子闻之，起于（鲁），齐行十日十夜而至于郢，见公输盘。公输盘曰：“夫子何命焉为？”子墨子曰：“北方有侮臣，愿藉子杀之！”公输盘不说。子墨子曰：“请献十金。”公输盘曰：“吾义固不杀人。”子墨子起，再拜曰：“请说之。吾从北方闻子为梯，将以攻宋。宋何罪之有？荆国有余于地，而不足于民。杀所不足，而争所有余，不可谓智；宋无罪而攻之，不可谓仁；知而不争，不可谓忠；争而不得，不可谓强；义不杀少而杀众，不可谓知类。”公输盘服。子墨子曰：“然乎？不已乎？”公输盘曰：“不可。吾既已言之王矣。”子墨子曰：“胡不见我于王？”公输盘曰：“诺。”

子墨子见王，曰：“今有人于此，舍其文轩，邻有敝舆，而欲窃之；舍其锦绣，邻有短褐，而欲窃之；舍其粱肉，邻有糠糟，而欲窃之。此为何若人？”王曰：“必为窃疾矣。”子墨子曰：“荆之地方五千里，宋之地方五百里，此犹文轩之与敝舆也；荆有云梦，犀兕麋鹿满之，江汉之鱼鳖鼋鼍为天下富，宋所为无雉兔狐狸者也，此犹粱肉之与糠糟也；荆有长松、文梓、楩楠豫章，宋无长木犹锦绣之与短褐也。臣以三事之攻宋也，为与此同类。”王曰：“善哉！虽然，公输盘为我为云梯，必取宋。”

于是见公输盘，子墨子解带为城，以牒为械，公输盘九设攻城之机变，子墨子九距之。公输盘之攻械尽，子墨子之守圉有余。公输盘诎，而曰：“吾知所以距子矣，吾不言。”子墨子亦曰：“吾知子之所以距我，吾不言。”楚王问其故，子墨子曰：“公输子之意，不过欲杀臣。杀臣，宋莫能守，可攻也。然臣之弟子禽滑厘等三百人，已持臣守圉之器，在宋城上而待楚寇矣。虽杀臣，不能绝也。”楚王曰：“善哉！吾请无攻宋矣。”

子墨子归，过宋，天雨，庇其闾中，守闾者不内也。故曰：治于神者，众人不知其功，争于明者，众人知之。（《墨子·公输》）

（3）范进因没有盘费，走去同丈人商议，被胡屠户一口啐在脸上，骂了一个狗血喷头道：“不要失了你的时了！你自己只觉得中了一个相公，就‘癞虾蟆想吃起天鹅肉’来！我听见人说，就是中相公时，也不是你的文章，还是宗师看见你老，不过意，舍与你的。如今痴心就想中起老爷来！这些中老爷的都是天上的‘文曲星’！你不看见城里张府上那些老爷，都有万贯家私，一个个方面大耳。像你这尖嘴猴腮，也该撒抛尿自己照照！不三不四，就想天鹅屁吃！趁早收了这心，明年在我们行事里替你寻一个馆，每年寻几两银子，养活你那老不死的老娘和你老婆是正经！你问我借盘缠，我一天杀一个猪还赚不得钱把银子，都把与你去丢在水里，叫我一家老小嗑西北风！”一顿夹七夹八，骂的范进摸门不着。

…………

胡屠户道：“我那里还杀猪，有我这贤婿，还怕后半世靠不着也怎的？我每常说，我的这个贤婿，才学又高，品貌又好，就是城里头那张府、周府这些老爷，也没有我女婿这样一个体面的相貌！你们不知道，得罪你们说，我小老这一双眼睛，却是认得人的，想着先年，我小女在家里长到三十多岁，多少有钱的富户要和我结亲，我自己觉得女儿像有些福气的，毕竟要嫁与个老爷，今日果然不错！”说罢，哈哈大笑。（《儒林外史》第三回）

（4）有钱富翁于客座中偶放一屁。适有二客在旁，一客曰：“屁虽响，不闻有一毫臭气。”一客曰：“不独不臭，还有一种异样香味。”富翁愁眉曰：“我闻得屁不臭，则五脏内损，死期将近，吾其死乎？”一客用手空招，用鼻连嗅曰：“才臭将来了。”一客以鼻皱起，连连大吸，又以手掩鼻蹙额曰：“我这里臭得更狠。”（《笑得好·臭得更狠》）

2.使用反证法或者归谬法证明下面的定理。

（1）《高中数学·必修5》（人教版）中的“均值定理”证明：

如果a，b∈R^+，那么

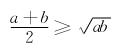
当且仅当a=b时，等号成立。

（2）《高中数学·选修2—2》（人教版）中：证明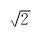不是有理数。