第8章 刘维尔
04-13Ctrl+D 收藏本站
约瑟夫·刘维尔（1809—1882）
普遍性成为现代分析学的核心，这是在柯西极限定理或黎曼积分中已经明显呈现的一种潮流。这两位超越他们前辈的数学家定义了包容一切的关键性概念，并且在此基础上引出普遍性结论，这些结论不仅对于一两个孤立事例成立，而且对于数量庞大的事例群体也是正确的。这是分析学中一项最有意义的进展。
此外，人们在17世纪还目睹了看起来仿佛相反的一种现象，那就是明显的例子和特殊的反例在分析学中的重要性日益增加。同前面几章讨论的普遍性定理一样，这种趋势同样值得我们注意。在这一章，我们首先考察约瑟夫·刘维尔于1851年发现的第一个超越数；在下一章再探讨卡尔·魏尔斯特拉斯在1872年提出的令人惊讶的病态函数。这两个结果分别是它们所处时代的巨大成就，并且提醒我们，在分析学的结论中，只要没有由独特的例子提供的说明，那么就是不完全的。
为了研究超越数，我们需要对这一问题的背景有所了解，考察一下它是从哪里提出来的，在以往的数十年中是如何得到提炼的，以及它的解决为什么成为一项如此重大的成就。按照微积分自身的演进过程，我们从17世纪开始。
代数数与超越数
似乎莱布尼茨是首次提出超越量概念的人，因为他在一个数学分类方案中使用了“超越的”这个术语。在论及他新发明的微分法时，莱布尼茨指出它的应用范围包括分式、根式以及类似的代数量，但是接着就补充道：“显然，我们的方法也适用于超越曲线，这种曲线不能通过代数运算加以简化，或者没有特定的次数，因此，这种方法是一种行之有效的最普遍的方法。” 1 从这里看出，莱布尼茨想要把那些属于代数范畴的对象，因而是相当简单明了的实体，同那些在本质上更为复杂的对象区分开来。
1 Dirk Struik, “The origin of l'Hospital's rule”, Mathematics Teacher, vol. 56 (1963), p. 276。
这种区分在18世纪由欧拉进一步完善。欧拉在其著名的《无穷小分析引论》一书中，把“加法、减法、乘法、除法、自乘和求根”以及“方程求解”列为所谓的代数运算，而把其他任何运算归入超越运算，如像那些涉及“指数和对数的运算，以及积分学中提供的其他大量运算”。2 他甚至走得更远，直到提出超越量，并且举出“不是基数乘方的数的对数”作为超越量的一个例子，不过他没有提供严谨的定义，也没有给出严格的证明。3
2 Leonhard Euler, Introduction to Analysis of the Infinite, Book I, p. 4。
3 Leonhard Euler, Introduction to Analysis of the Infinite, Book I, p. 80。
我们的数学先哲们往往具有正确的思想，即使他们未能把那种思想准确地表达出来。对于他们而言，某些数学对象，例如曲线、函数或者数字，明显是可以通过基本代数运算得到的，而其他的对象则是异常复杂的，以至全然超越了代数运算，并因此而获得“超越”这个名称。
到18世纪后期，在勒让德这样一些数学家的著作中，出现了一种无歧义的定义。一个实数如果是某个具有整系数的多项式方程的解，就把它称为代数数。这就是说，对于一个数x0，如果存在一个多项式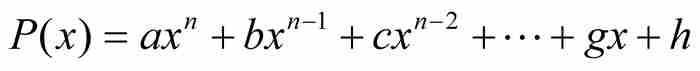
，其中a, b, c, …, g和h为整数，满足
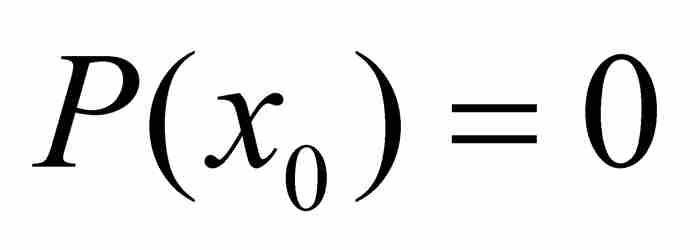，那么x0是一个代数数。例如，
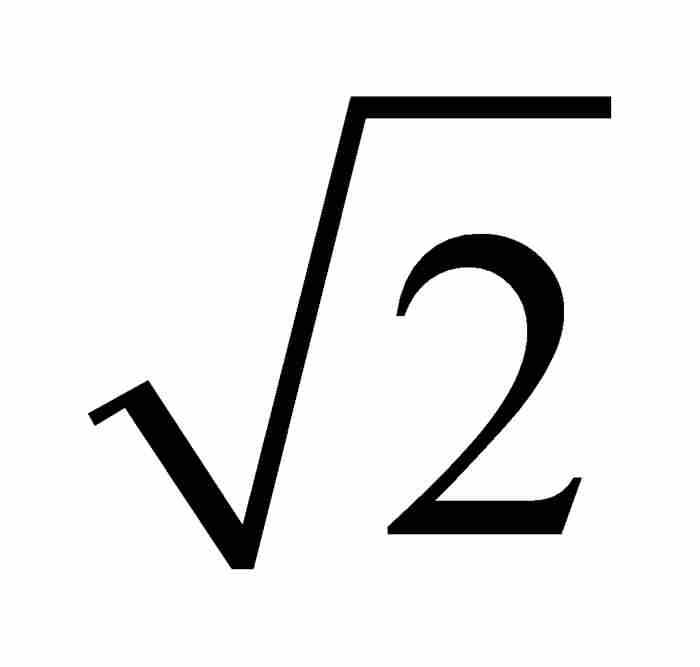是代数数，因为它是整系数二次方程
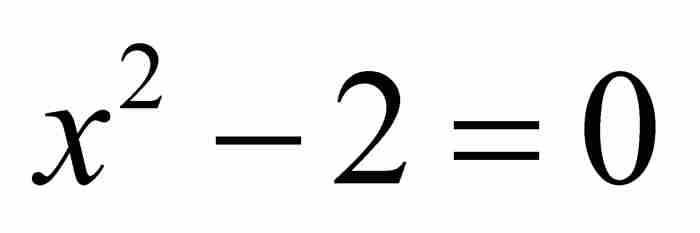的一个解。
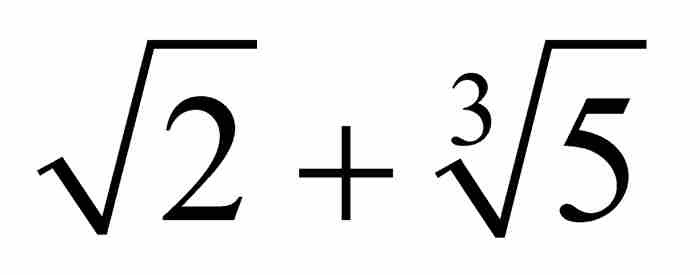也是代数数，不过，这看起来不是那么明显，因为它是整系数6次方程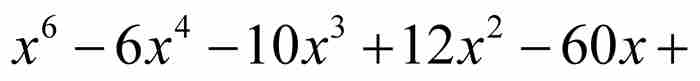
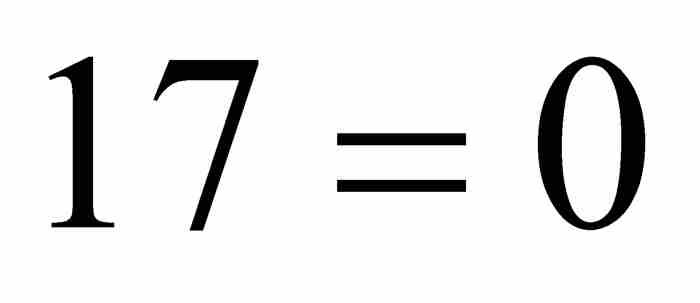的一个解。
从几何学观点看，一个代数数乃是函数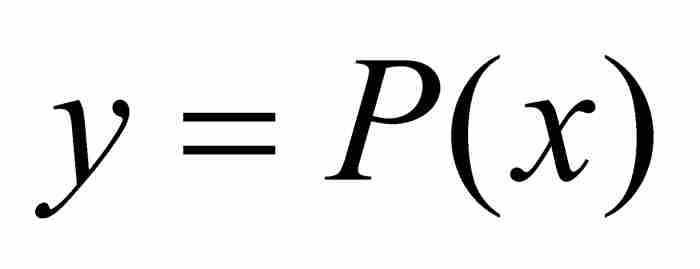
的图形的x截距，其中P是一个具有整系数的多项式（参见图8-1）。如果设想在同样的坐标系中画出系数为整数的所有线性式、二次式和三次式以及一般情况下的所有多项式的图形，那么它们的x截距的无穷集合都是代数数。
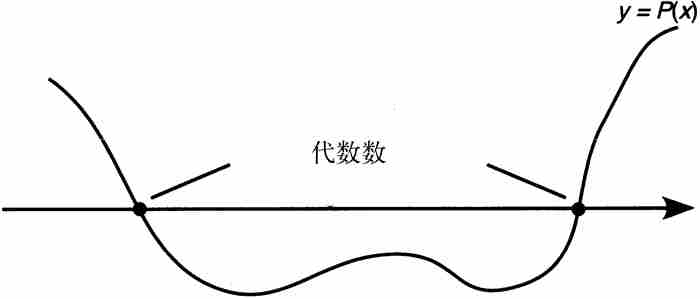
图 8-1
这就提出一个显而易见的问题：还存在任何其他代数数吗？为了考虑这种可能性，我们姑且说，一个实数只要不是代数数，那么它就是超越数。单纯从逻辑上说，任何实数必定属于这两类数中的一类。
然而，果真存在超越数吗？毕竟，定义一个术语并不能就保证它的实体的存在。正如一位哺乳动物学家，完全可以把一头栖息于水中的海豚定义为“代数海豚”，而把不在水中生活的海豚定义为“超越海豚”。这里，超越海豚这个名称在概念上是无歧义的，但是并不存在这样一个物种。
数学家们必须面对同样的可能性。那么，超越数是否只是全凭想象而精心定义的一种虚构的数呢？要是这样，所有代数数的x截距能够完全布满x轴这条直线吗？如果不能，我们又从哪里去寻找一个不等于任何整系数多项式方程的x截距的数呢？
作为走向答案的第一步，我们注意到，一个超越数必定是无理数。这是因为，如果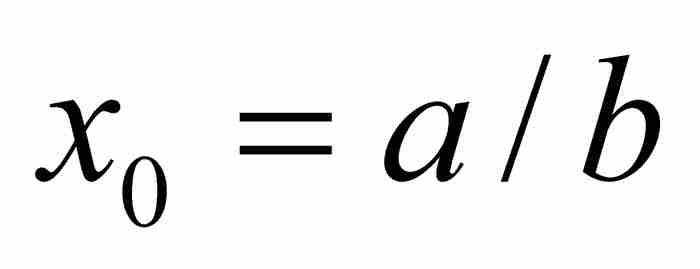
是有理数，那么
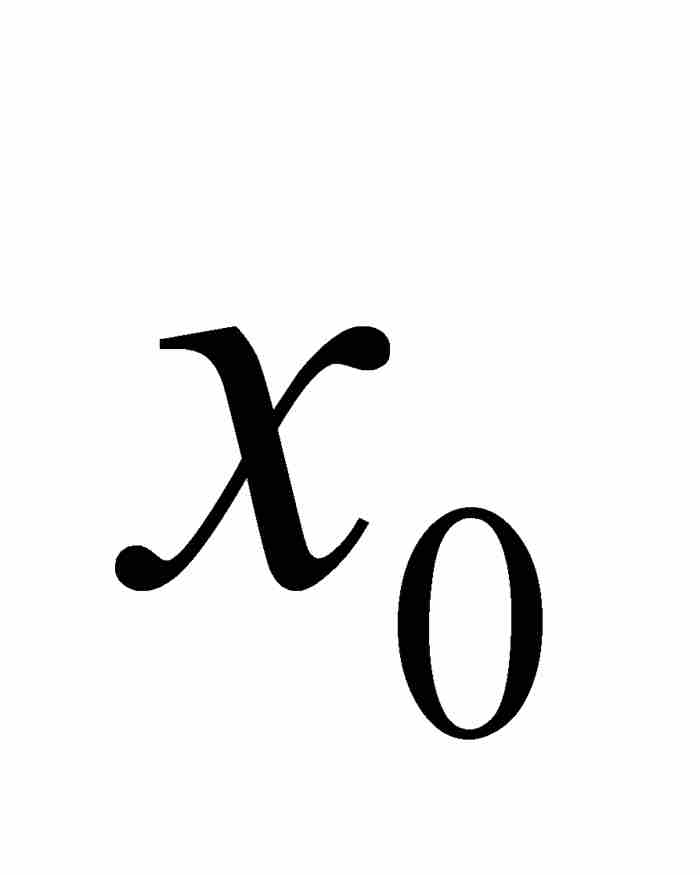显然满足一次方程
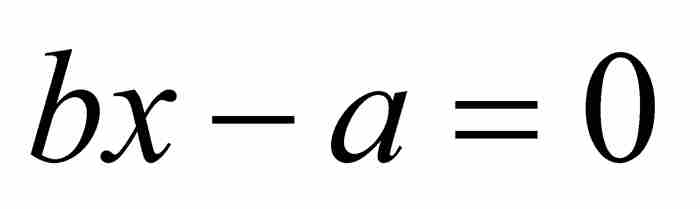，它的系数b和-a为整数。事实上，有理数恰好就是满足整系数线性方程的那些代数数。
自然，并非每个代数数都是有理数，从前面提到的无理数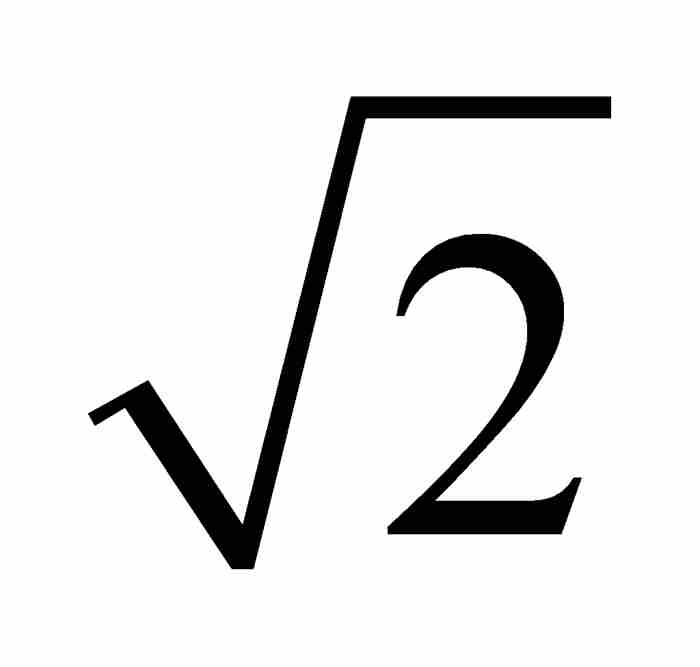
和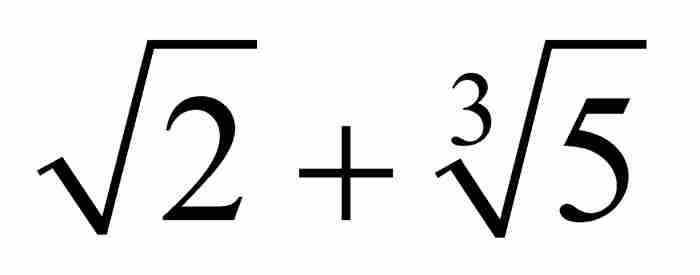
这样的代数数中，我们清楚地看出这一点。因此，代数数代表着有理数的某种扩充，其中取消它们作为一次整系数多项式方程之解的条件，但是仍然保留多项式系数为整数的限制。
由此可见，如果超越数存在，它们必定隐藏在无理数中间。从古希腊起，人们就知道像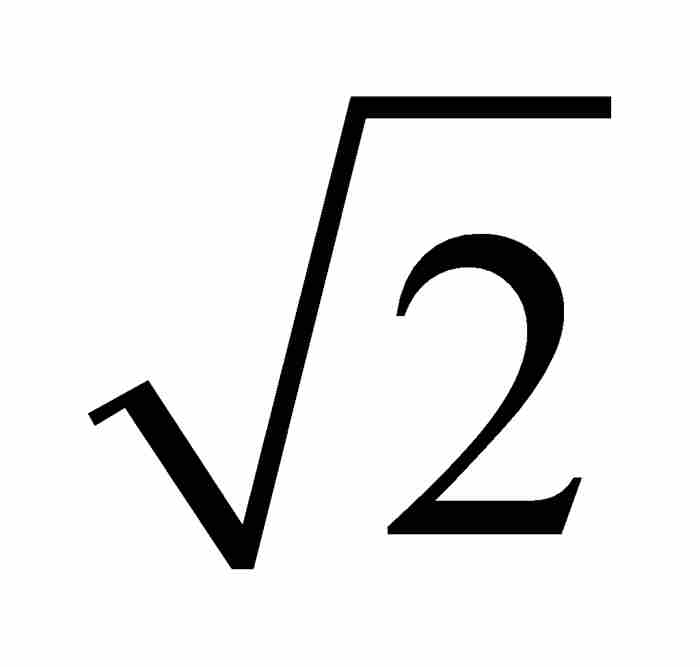
这样的方程的根是无理数，而到18世纪末，e和π这两个常数为无理数分别由欧拉于1737年和约翰·兰伯特（1728—1777）于1768年证实。4 不过，同证明一个数是超越数比较起来，证明一个数是无理数要容易得多。
4 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, pp. 459-460。
正如我们所提到的，欧拉曾经猜测log23是超越数，而勒让德相信π也是超越数。5 然而，无论数学家们的信念多么强烈，却未能找到证明。直到19世纪中后期，甚至没有取得存在一个超越数的证明。到那时，依然有这样的可能性，这种超越数或许就像那些“超越海豚”一样，无非是臆想中的空中楼阁而已。
5 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 593。
最终，法国数学家约瑟夫·刘维尔提供了超越数的一个例子。如今的大学生们可能从微分方程的斯图姆 · 刘维尔理论或者从复分析中的刘维尔定理（“一个有界的整函数为常数”）记起他的名字。刘维尔在电学和热力学这样的应用科学领域也作出了重大贡献，同时他在1848年法国二月革命后的动荡年代投身政治活动，并且被选为法兰西议会议员，活跃在一个完全不同的舞台上。此外，他还创办了数学史上一本最具影响力的杂志，这本杂志原名为《纯粹数学与应用数学杂志》，但是人们通常简单地称之为《刘维尔杂志》。他主编这本杂志长达39年。刘维尔采用这种方式担负起向整个欧洲以及世界各地的同行传播数学思想的责任。6
6 刘维尔的这些工作以及他在其他方面的工作，在Jesper Lützen所写的科学家传记Joseph Liouville 1809—1882: Master of Pure and Applied Mathematics (Springer-Verlag, 1990)中有详尽论述。
在实分析领域，刘维尔以其两项重大发现而被人们永志不忘。第一，他证明了某些初等函数不可能存在初等原函数。任何学习过微积分的人都会记起运用一些巧妙的方法求不定积分。虽然这样的方法不再像以往那样是人们孜孜以求的，但是微积分教程仍然讲述诸如分部积分法和部分分式积分法一类的方法，以便使我们能够计算像
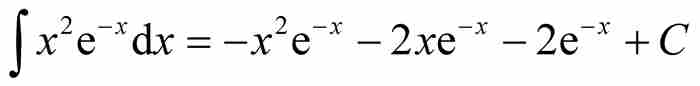
这样的原函数，或者像
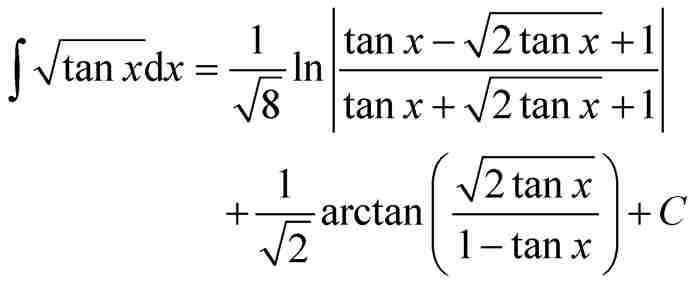
这种远非不言自明的原函数。请注意，在这两种情况下，被积函数和它们的原函数都是由标准欧拉函数集中的代数函数、三角函数、对数函数以及它们的反函数构成的。这样的积分都是原函数为“初等”函数的“初等”积分。
可惜的是，即使最勤奋的求积者，当他们欲求作为简单函数的有限组合的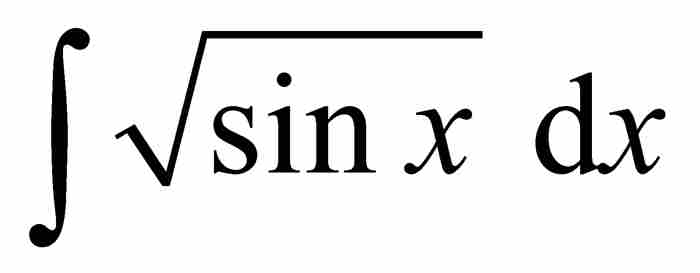
时，都会陷入困境。刘维尔找到了这个问题的原因。他在1835年的一篇文章中，证明了为什么某些积分不可能具备最终形式的答案。他写道，例如，“人们凭借我们的方法，很容易确信积分
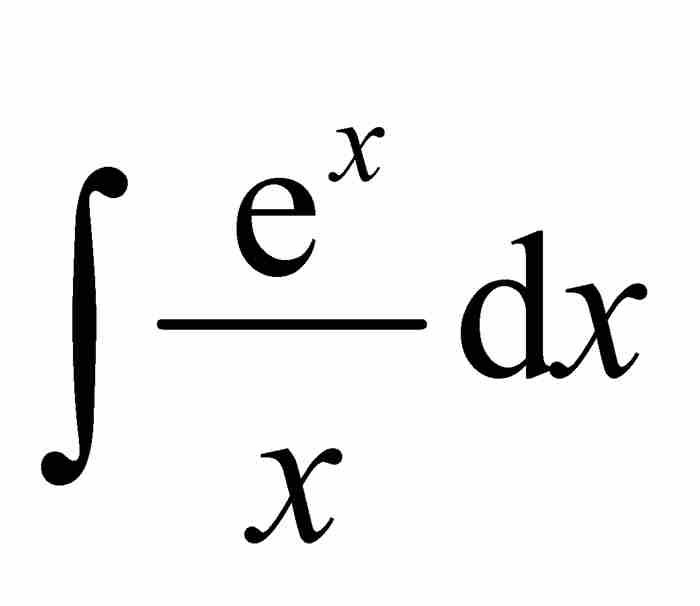不可能存在有限形式的原函数，而这个积分曾使几何学家们忙得不可开交”。7 从此，简单函数必然存在简单原函数的希望化为泡影。
7 E. Hairer and G. Wanner, Analysis by Its History, Springer-Verlag, 1996, p. 125。
我们在这一章的目标是考察刘维尔的另外一项重大的贡献，那就是存在超越数的证明。他的最初证明是在1844年给出的，不过他在1851年的一篇经典性论文中对结果作了改进和简化（这篇论文自然是发表在他创办的杂志上），我们从中摘出证明。8 在刘维尔给出他的闻所未闻的超越数例子之前，他必须首先证明一个重要的不等式，这个不等式涉及代数数无理数同它们邻近的有理数之间的关系。
8 J. Liouville, “Sur des classes très-étendues de quantités don't la valeur n'est ni algébrique, ni même réductible à des irrationnelles algébriques”, Journal de mathématiques pures et appliqués, vol. 16 (1851), pp. 133-142。
刘维尔不等式
正如我们指出的那样，如果一个实数是某个整系数多项式方程的解，那么它就是一个代数数。但是，这样一个方程的任何解，都是无限个方程的解。例如，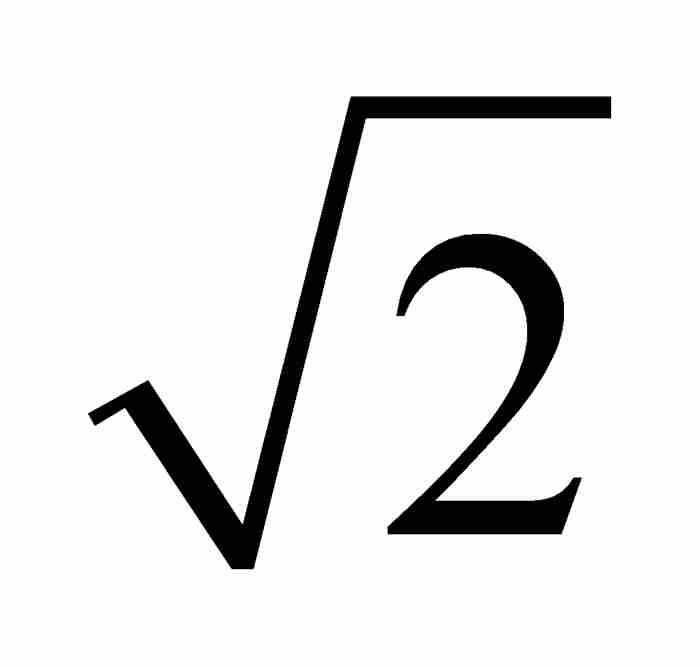
是二次方程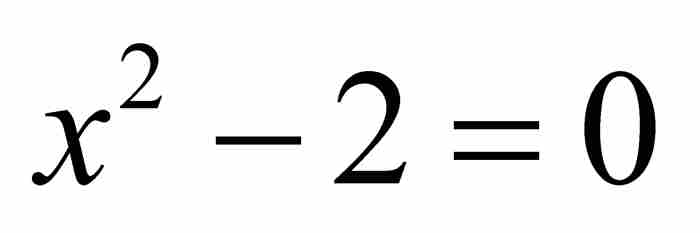
的解，它又是三次方程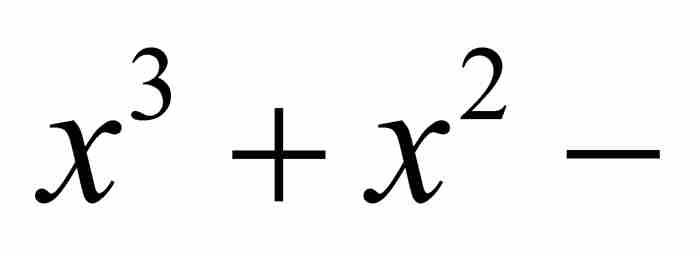
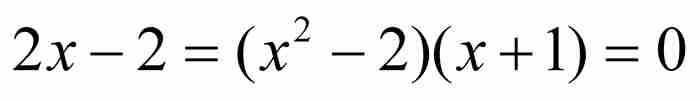的解，同样也是四次方程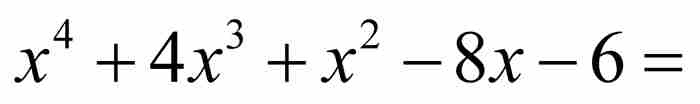
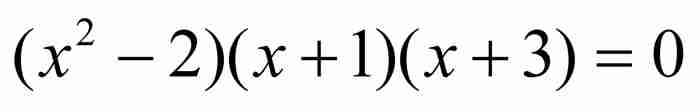的解，等等。于是，我们首先规定使用一个次数最低的多项式。所以，对于代数数
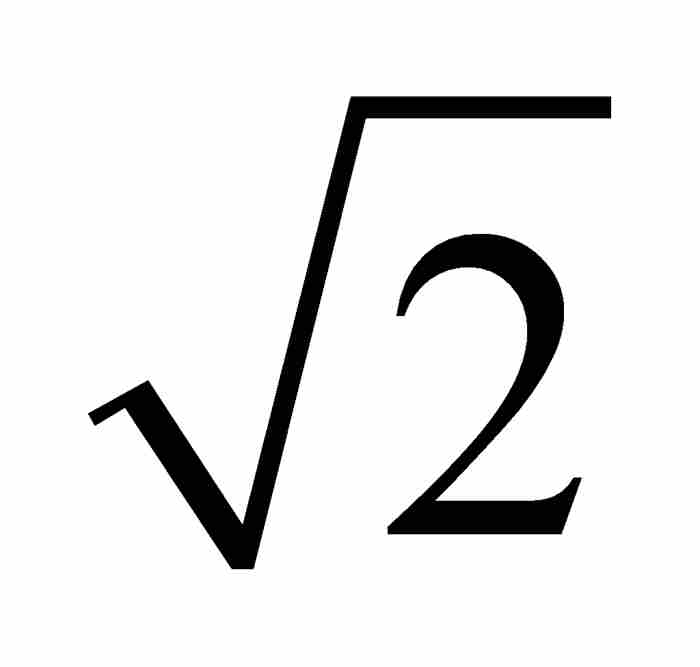而言，我们将采用上面的二次式而不是次数更高的同类多项式。
假定x0是一个无理数代数数。按照刘维尔的表示法，我们用
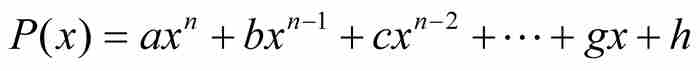（1）
表示它的次数最低的多项式，其中a, b, c, …, g, h为整数，n≥2（如果n=1，如像上面指出的那样，那么代数数是有理数）。由于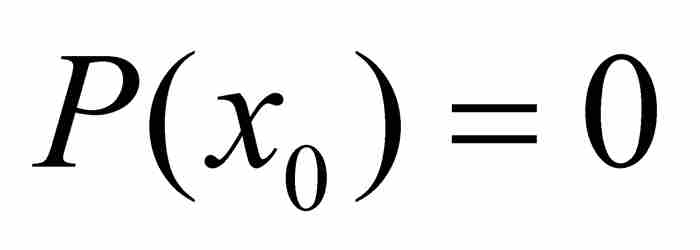
，用因式分解定理可以得到
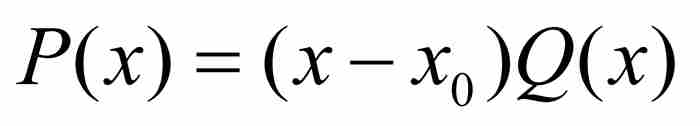（2）
其中Q(x)是一个n-1次多项式。刘维尔希望对于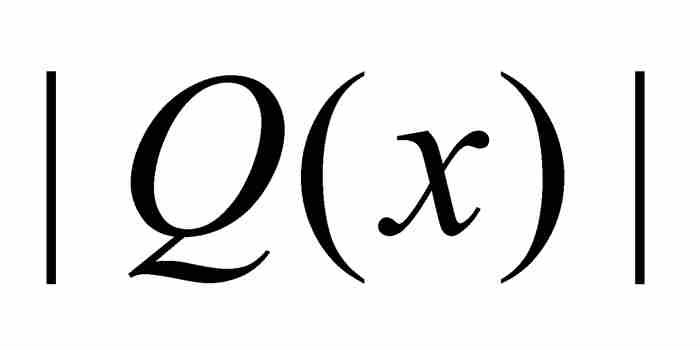
的值（至少对于Q在x0邻近的x的值）确定一个上界。我们先给出他的证明，然后提供一个更简单的替代证明。
刘维尔不等式 如果x0是次数最低的整系数多项式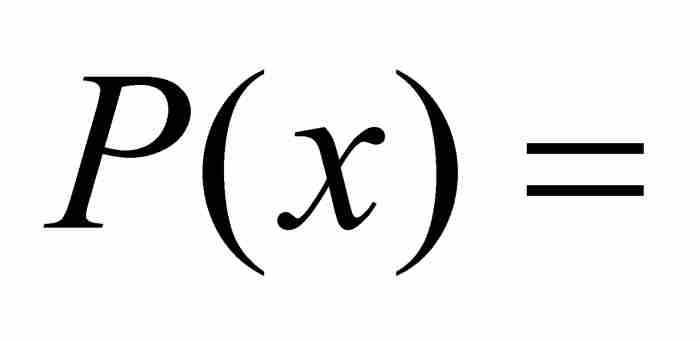
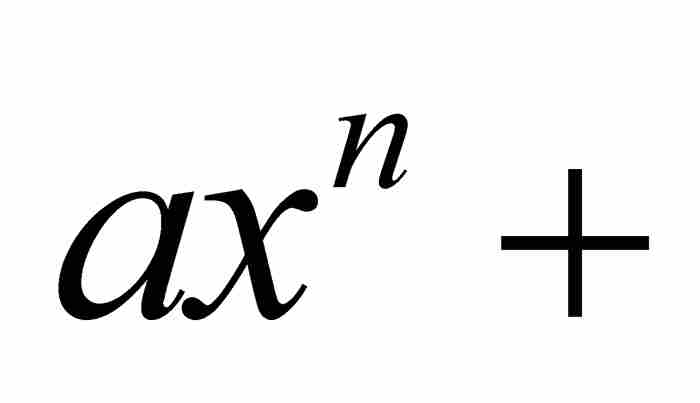
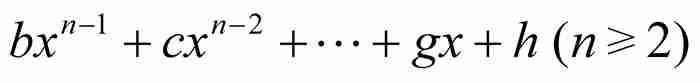的一个无理数代数数，那么存在这样一个实数A>0，只要p/q是区间
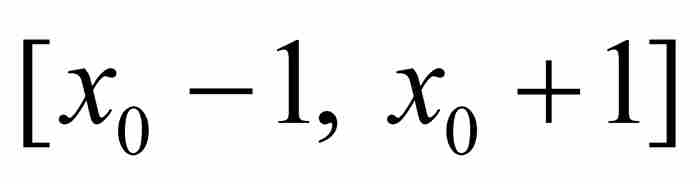内的一个有理数，就有
。
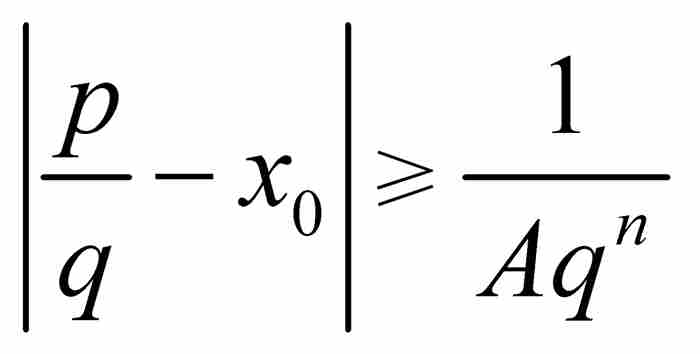证明 这个不等式的证明有其独特之处，我们从式（2）引入的实系数多项式Q(x)着手。Q在任何有限闭区间上是连续的，因而是有界的，所以存在一个A>0，对于区间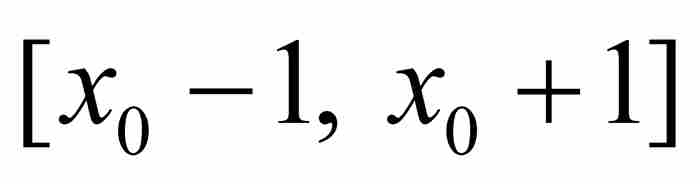
内的所有x，满足
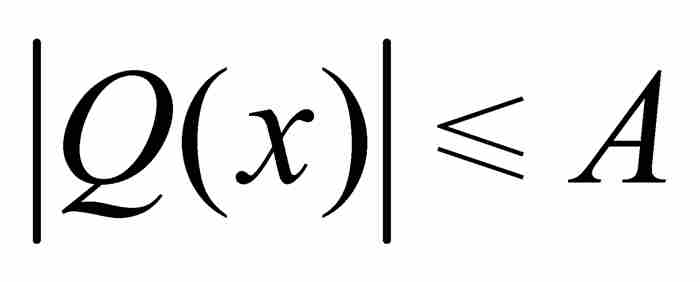（3）
现在考虑区间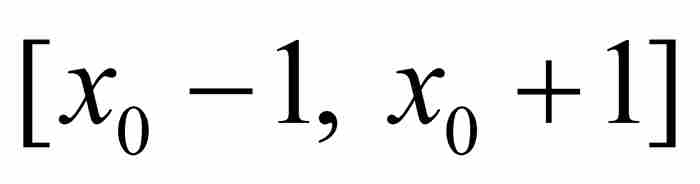
内的任何一个有理数p/q，其中我们要求这个有理数是最简形式，并且分母为正整数（即q≥1）。由式（3）看出
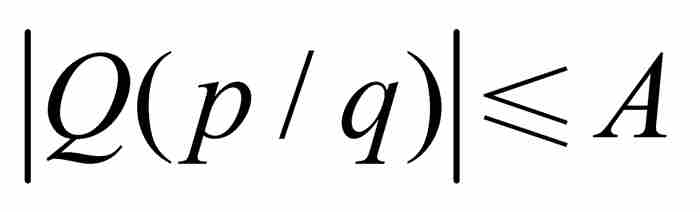，同时可以断言
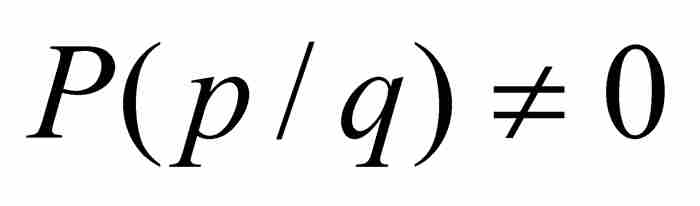，因为在相反的情况下能够分解因式，得到
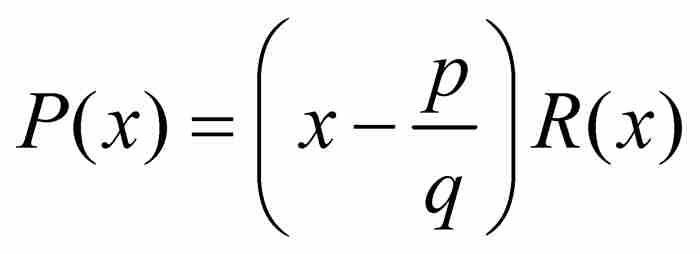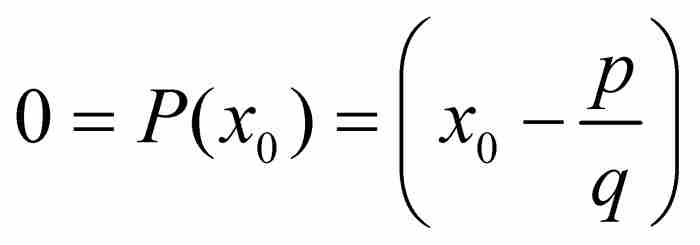
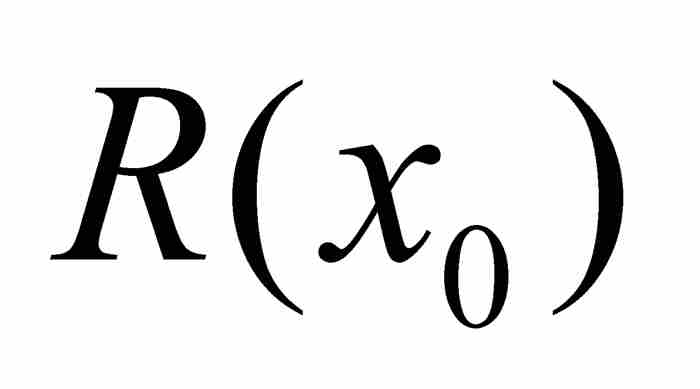，并且可以证明R(x)是一个n-1次整系数多项式。于是有
，并且有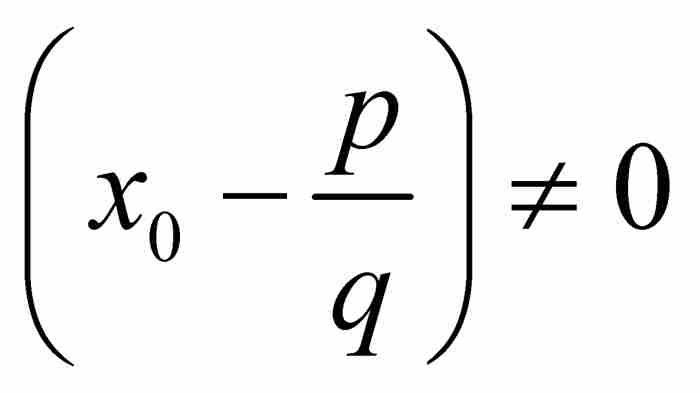
（因为有理数p/q不同于无理数x0），我们由此断定
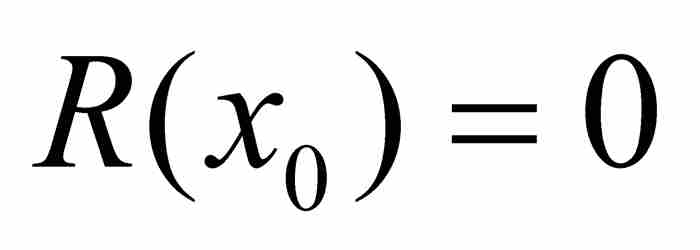。但是，这使x0成为
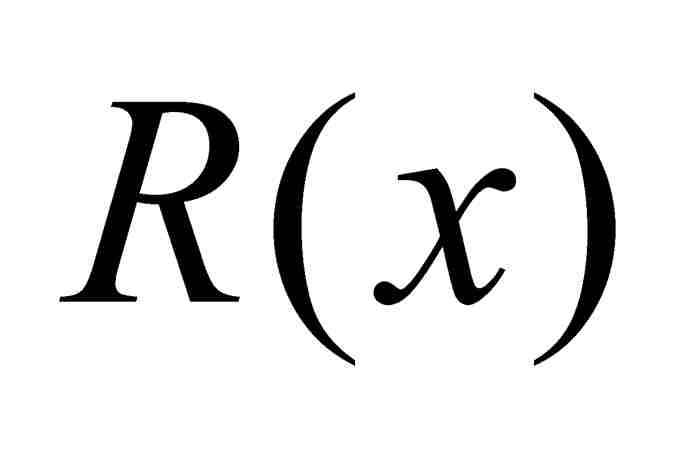的一个根，而R是次数小于P的一个整系数多项式，违反P是最低次多项式这个假定条件。这样推出p/q不是
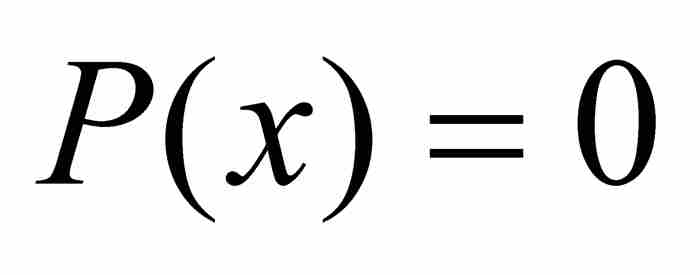的根。
刘维尔回到式（1）中的最低次多项式，并且给出定义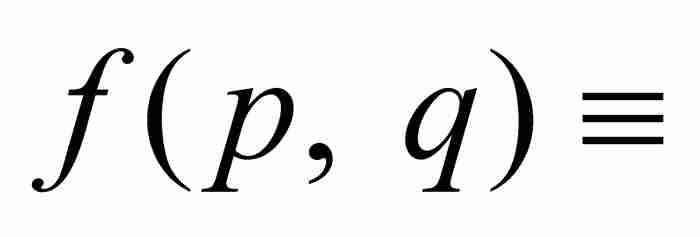
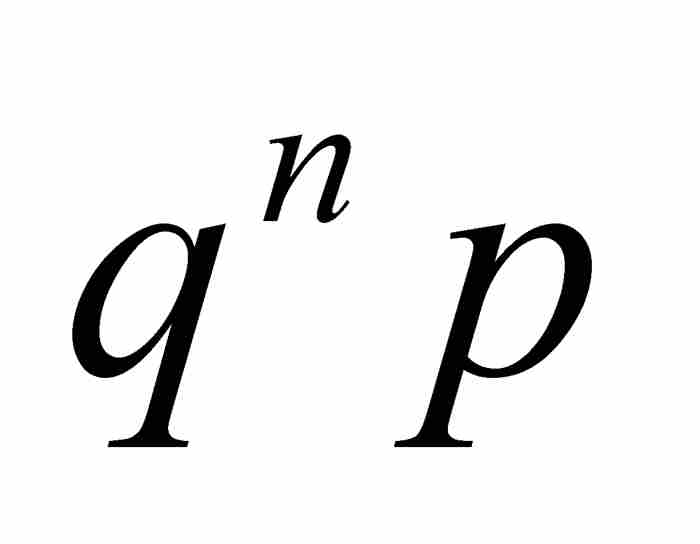
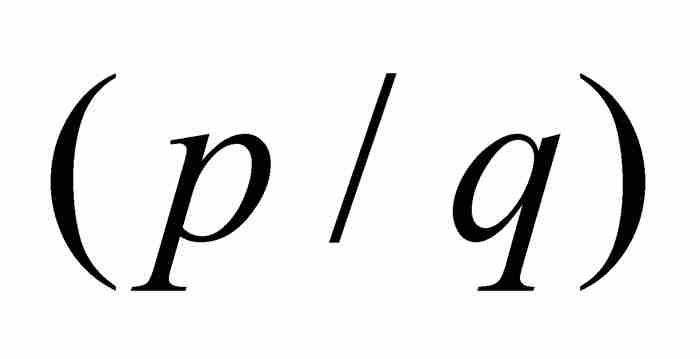。请注意，
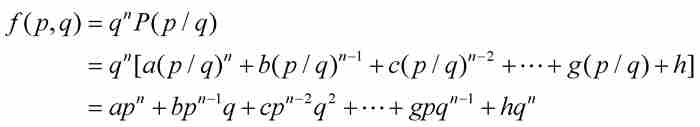（4）
他从式（4）作出两条简单然而具有说服力的说明。
第一，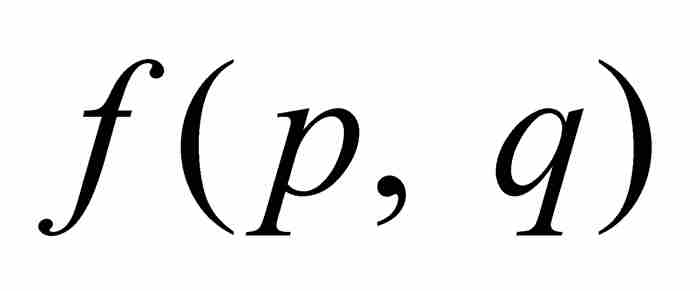
是一个整数，因为在其表达式中a, b, c, …, g，h以及p和q都是整数。第二，
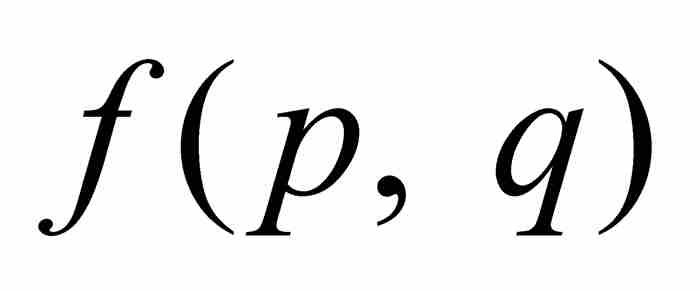不会为零，若不然，如果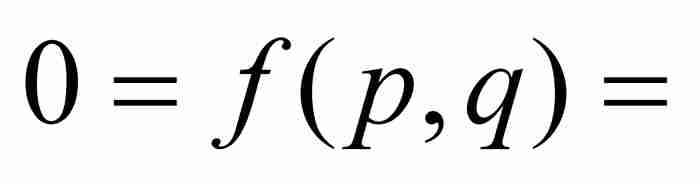
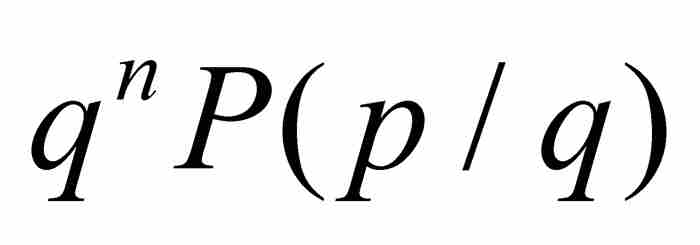，那么就有
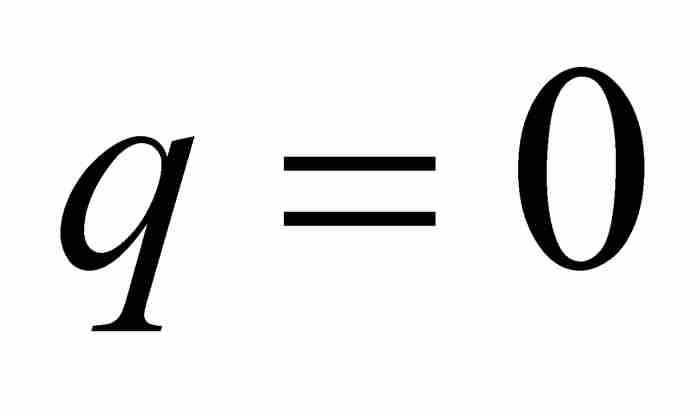或者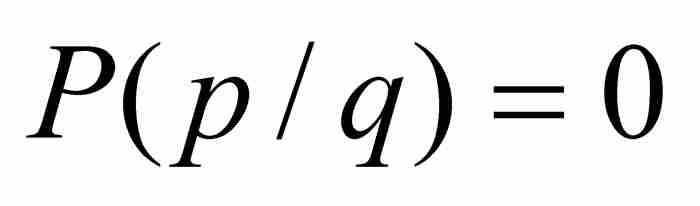
。前一种情况是不可能出现的，因为q是一个分母；至于后一种情况，从上面的讨论看出同样是不可能的。因此，刘维尔知道
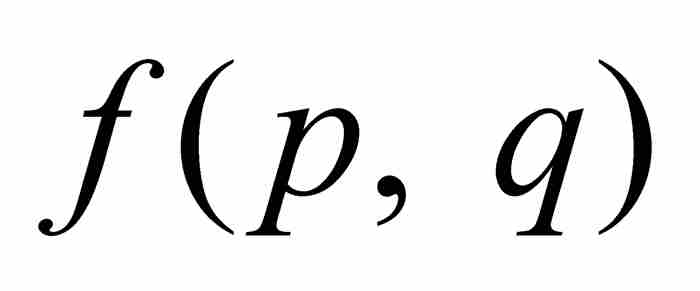是一个非零整数，他由此推出
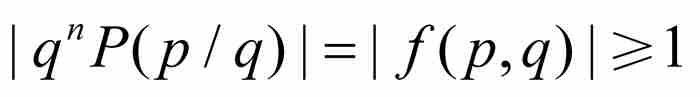（5）
定理证明的剩余部分很快就会得到。根据式(3)和式(5)以及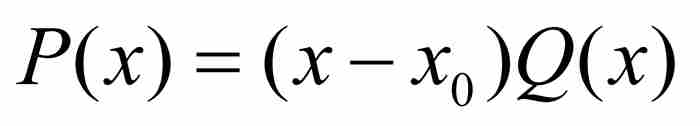
，他断定
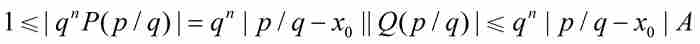
因此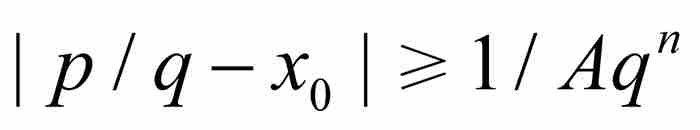
，而定理的证明得以完成。
在刘维尔的证明中，不等式所起的作用是引人瞩目的。所以人们有时把现代分析学称为“不等式的科学”，这是对分析学特征的恰如其分的表述，并且随着这个世纪的前进，这个特征日益显现出来。
我们前面说过对刘维尔定理给出一种替代证明。这一次，柯西中值定理在证明中扮演主角。1
1 这个证明是从George Simmons, Calculus Gems, McGraw-Hill, 1992, pp. 288-289改写成的。
我们把刘维尔不等式重述如下，然后给出新的证明。
刘维尔不等式 如果x0是具有最低次数的整系数多项式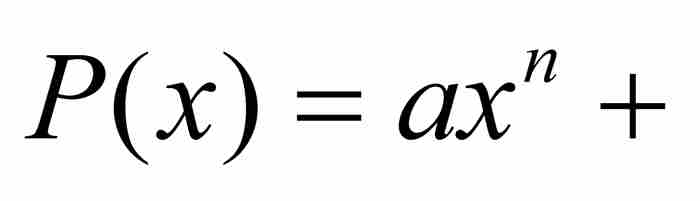
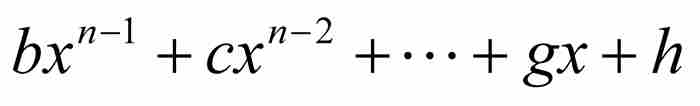和次数n≥2的一个无理数代数数，那么存在这样一个实数
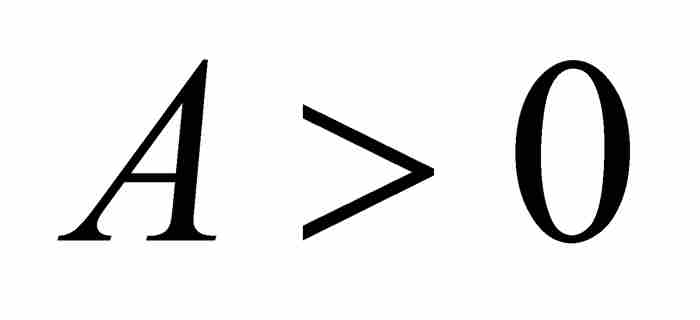，只要p/q为区间
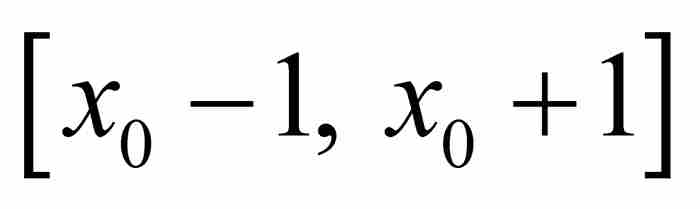内的一个有理数，就有
。
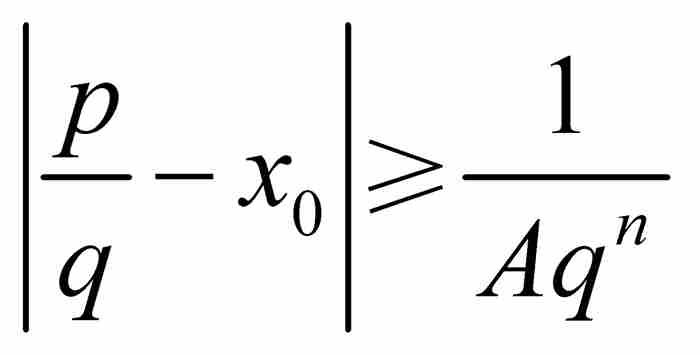证明 对多项式P求导，我们得到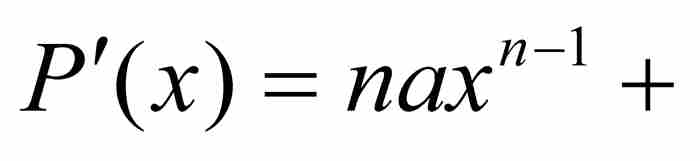
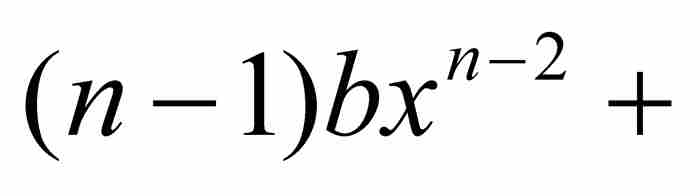
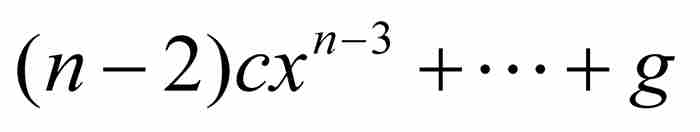。这个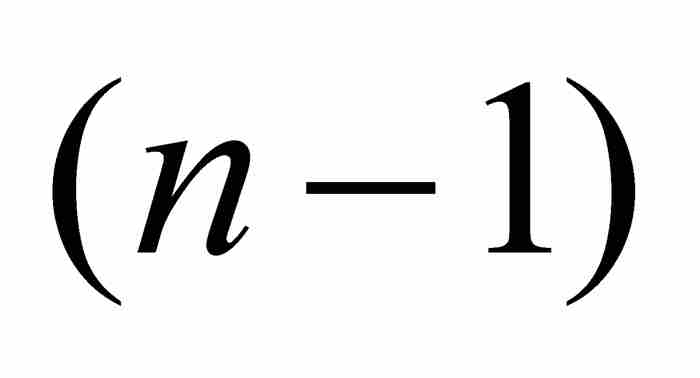
次多项式在区间
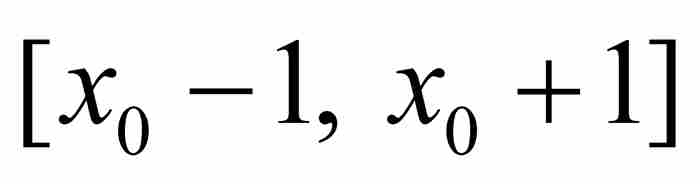上是有界的，所以存在一个
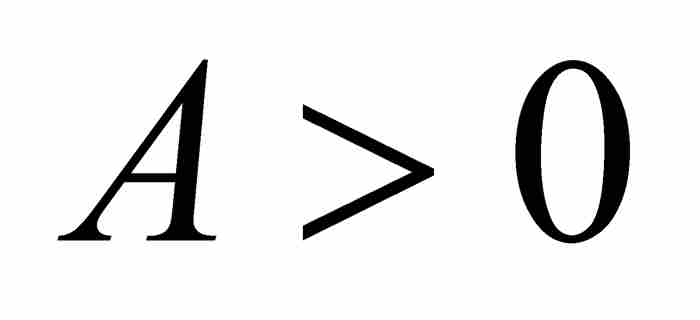，使得
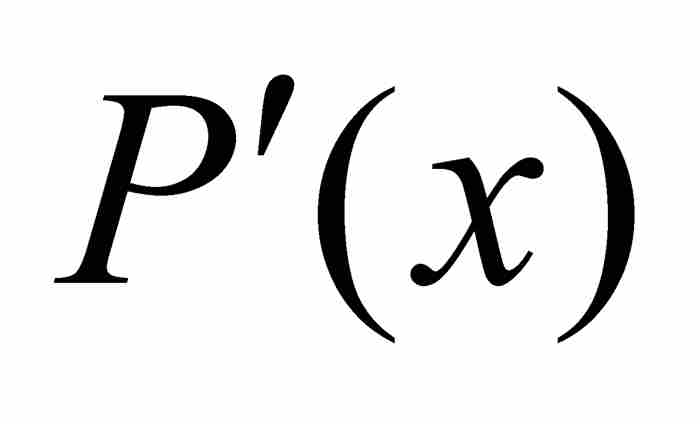在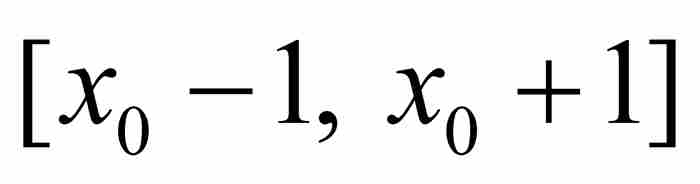
上以A为界，即对于所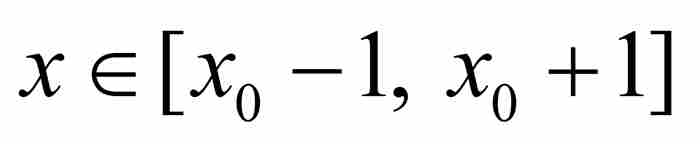有
有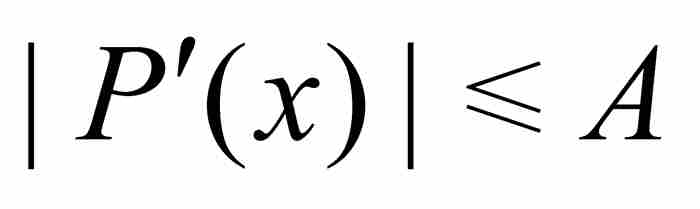
。令p/q是
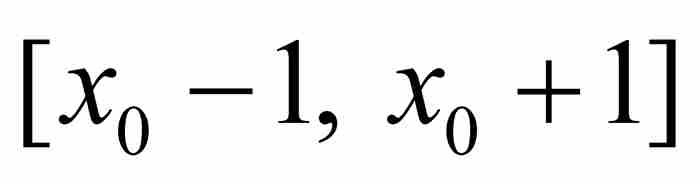内的一个有理数，并且对P应用柯西中值定理，可知在
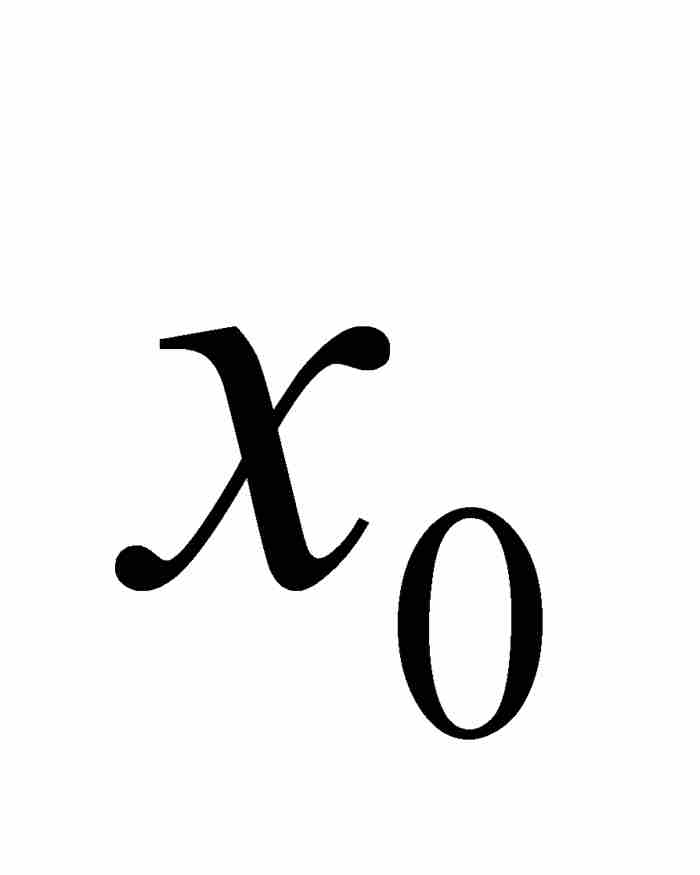和 p/q之间存在一点c，满足
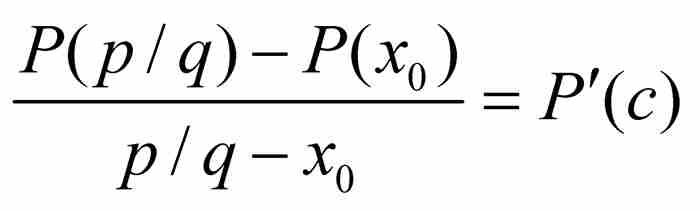（6）
已知
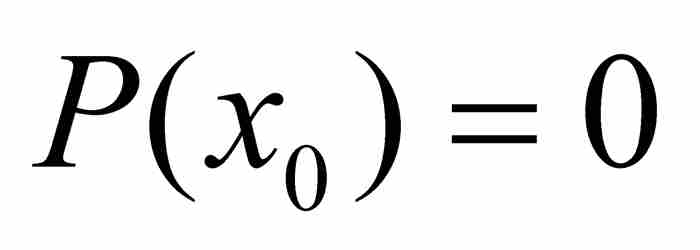，而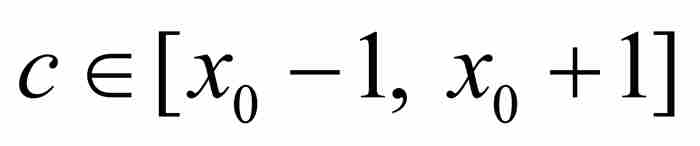
，由式（6）看出
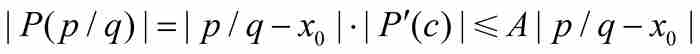
由此得到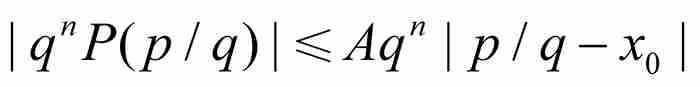
。但是，正如前面指出的那样，
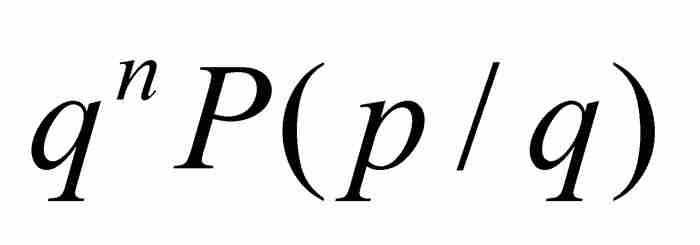是一个非零整数，所以
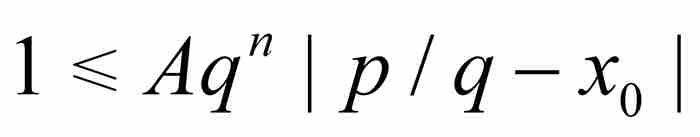。这就推出刘维尔不等式。
在此，举一个例子或许有助于理解。我们考虑无理数代数数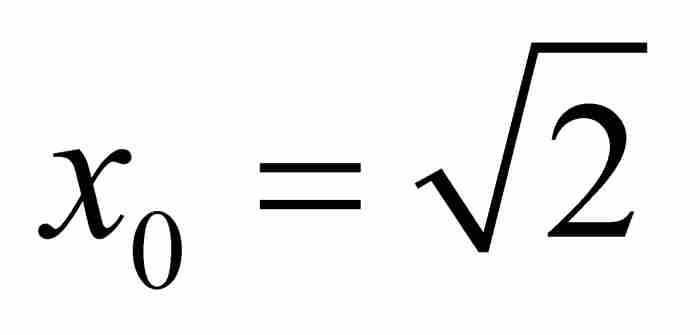
。这时最低次多项式为
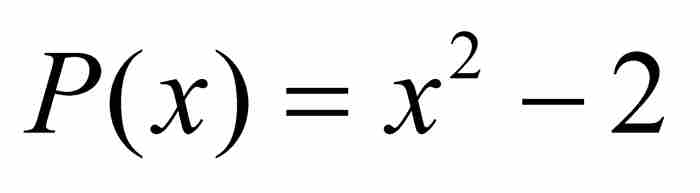，它的导数是
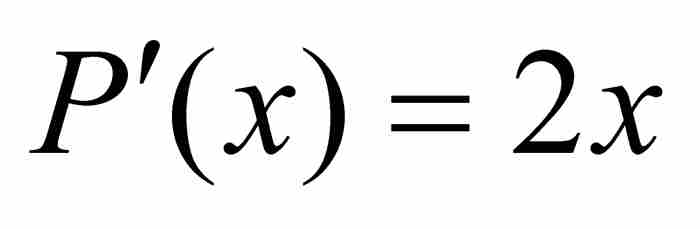。显然，在区间
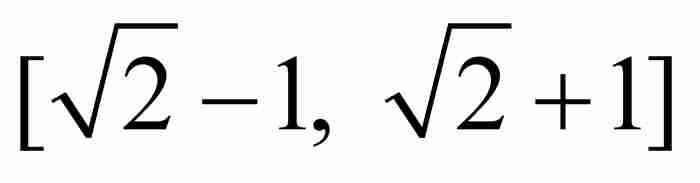上
以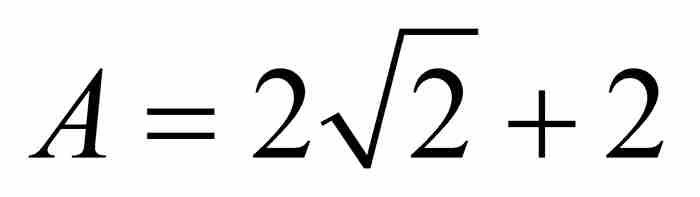
为界。刘维尔不等式表明，如果p/q是这个闭区间内的任何有理数，那么
。
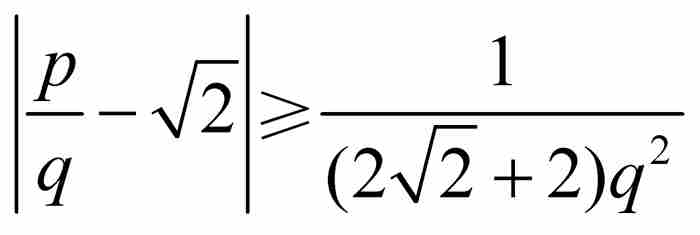这一点可望从数值趋势上得到证实，例如，对于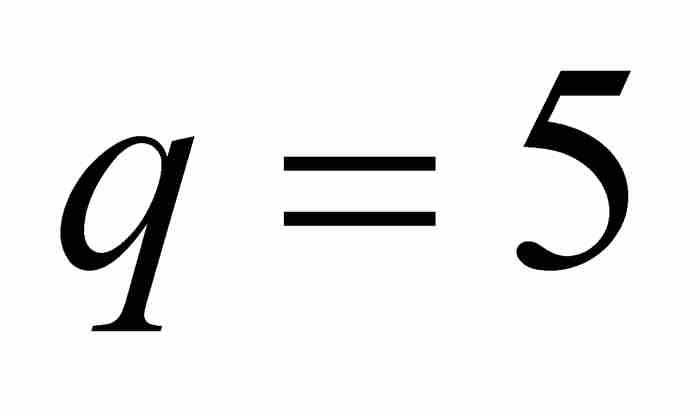
的情形，不等式变为
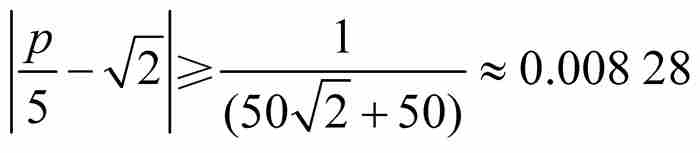。然后，我们检验区间
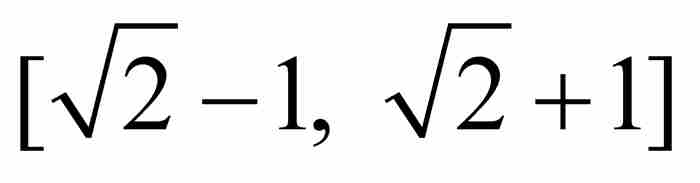内所有“1/5”处的点。所幸这样的分数仅有10个，而且它们全部满足刘维尔不等式：
p/5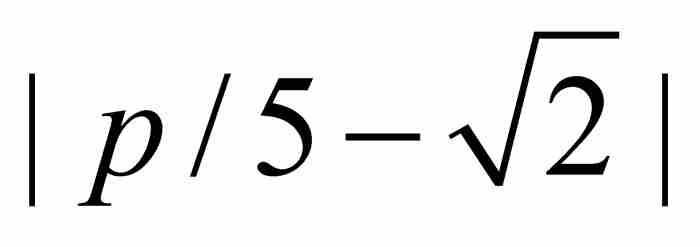
----------------------------------- 3/5=0.600.8142 4/5=0.800.6142 5/5=1.000.4142 6/5=1.200.2142 7/5=1.400.0142 8/5=1.600.1858 9/5=1.800.385810/5=2.000.585811/5=2.200.785812/5=2.400.9858
这个例子同时也暗示：通常我们可以取消要求p/q接近x0的限制。就是说，我们指定A*为大于1和A的数，其中A是像上面那样确定的。如果p/q是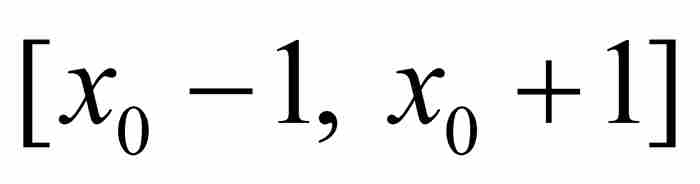
内的一个有理数，那么由于A*≥A而有
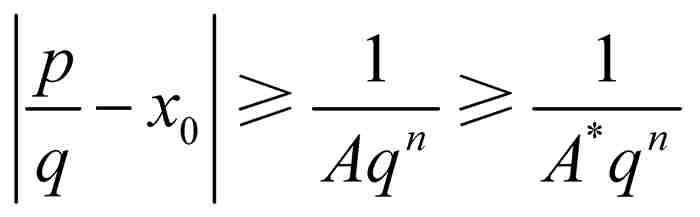
另一方面，如果p/q是区间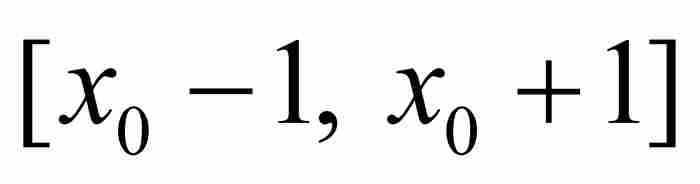
之外的一个有理数，那么由于A*≥1和q≥1，同样有
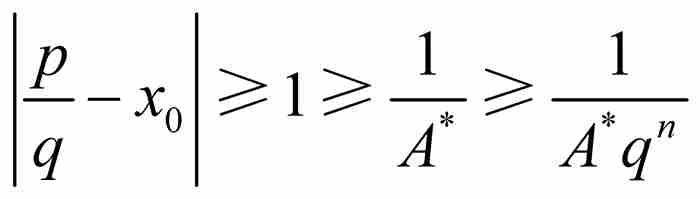。最后这项结果说明，存在一个A* > 0满足
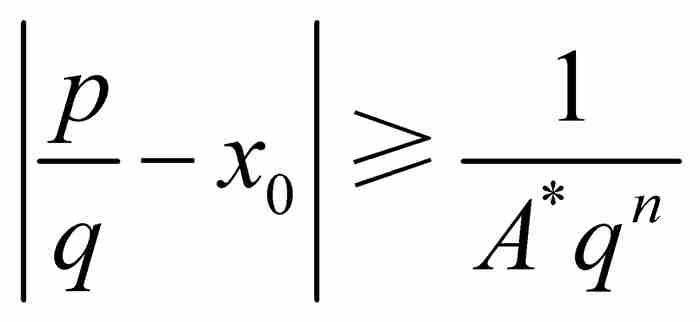，而同p/q对x0的接近程度无关。
通俗地讲，刘维尔不等式向我们表明，有理数作为无理数代数数的邻居，其数量是少得可怜的，因为在一个无理数x0同任何有理数p/q之间必定至少存在一个大小为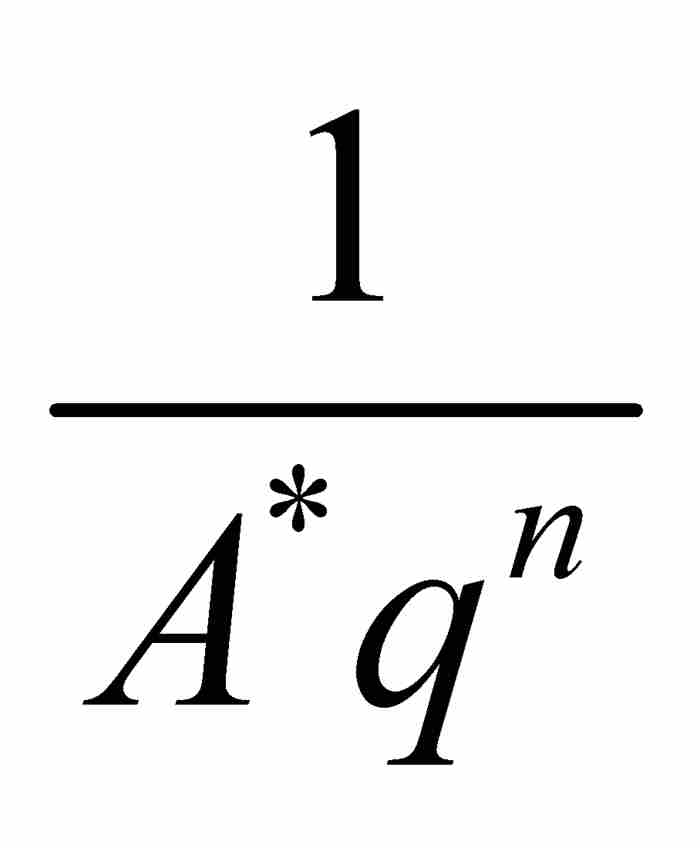
的空隙。我们很难想象刘维尔是怎样注意到这一点的。他走到了这一步，并且提供了一个巧妙的证明，这是他的卓越数学才能的一次展现。然而，倘若他不再迈出下面这一步，这一切也许早已被人们遗忘：他利用他获得的结果找到了世界上第一个超越数。
刘维尔超越数
我们首先提出关于推理策略的一个词汇——“不相容”。刘维尔找到的是一个同上述不等式的结论不相容的无理数。这个无理数因而违反刘维尔不等式的假定，这就意味着它不是代数数。只要刘维尔能够完成这项艰巨的任务，他就捕捉到一个特定的超越数。令人非常吃惊的是，他恰好做到了这一点。1
1 J. Liouville, “Sur des classes très-étendues de quantités don't la valeur n'est ni algébrique, ni même réductible à des irrationnelles algébriques”, Journal de mathématiques pures et appliqués, vol. 16 (1851), pp. 133-142。
定理 实数
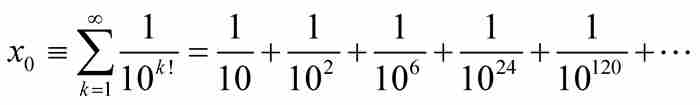
是超越数。
证明 有三个问题有待解决，我们依次一步处理一个问题。
第一步，我们断言定义x0的级数是收敛的。这个结论很容易从判别级数收敛的比较检验法推出。也就是说，
保证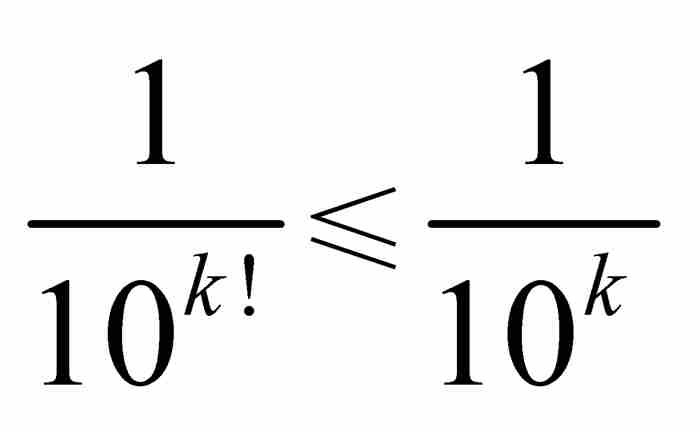
，而这个条件使级数
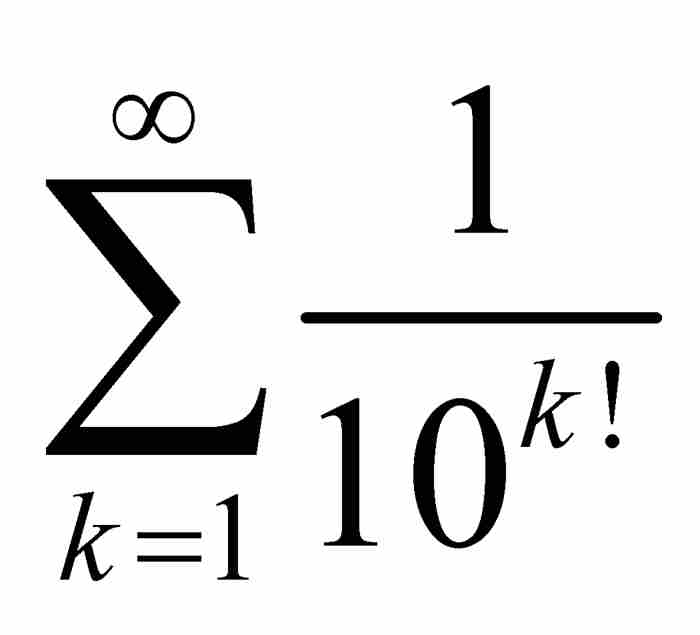成为收敛级数，因为
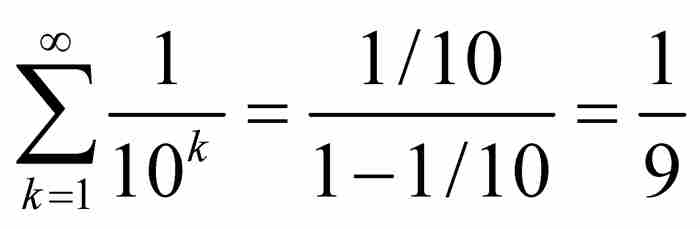是收敛级数。简而言之，x0是一个实数。
第二步，我们断言x0是无理数。这一点是明显的，因为它的十进制小数表示为0.110 001 000 000 0…，其中的非零位分别是由1占据的小数后的第1位，第2位，第6位，第24位，第120位，等等，这些日渐孤单的1由越来越长的一串0分隔开来。显而易见，在这种十进制小数的展开式中，没有一段有限的数字是重复的，所以x0是无理数。
最后一步，证明刘维尔定义的数是超越数。这也是最困难的一步。为此，我们反过来假定x0是一个代数数无理数，它具有次数为n≥2的最低次多项式。根据刘维尔不等式，必定存在这样一个A* > 0，使得对于任意有理数p/q，有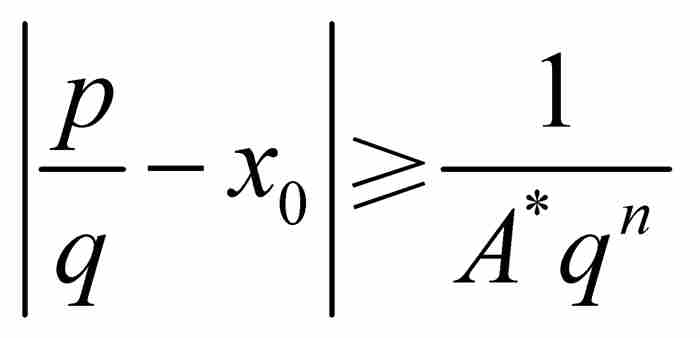
，因此，
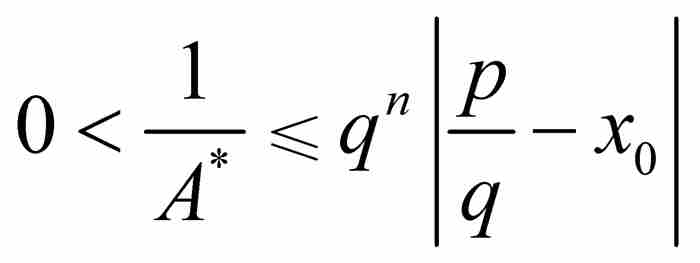（7）
我们现在选择一个任意的自然数m > n，并且考察部分和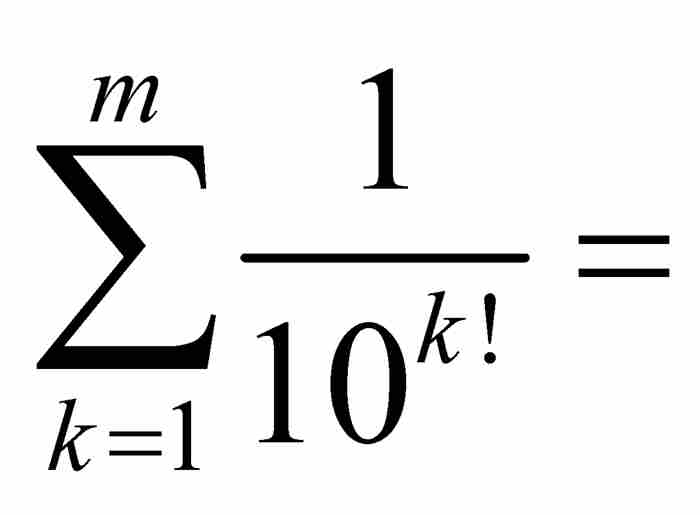
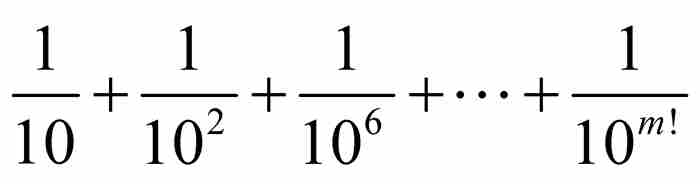。如果合并这些分式，它们的公分母将是10m!，所以我们可以把这个和式写成
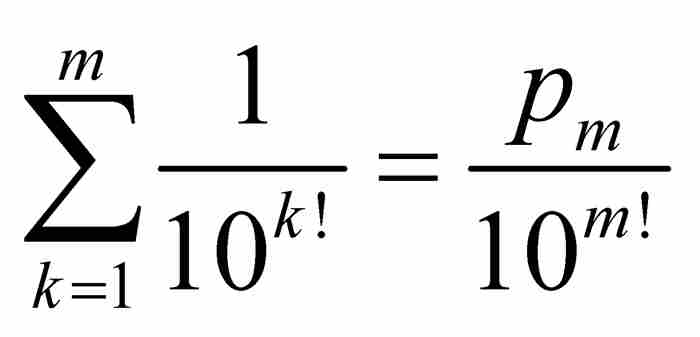，其中pm是一个自然数。因此，
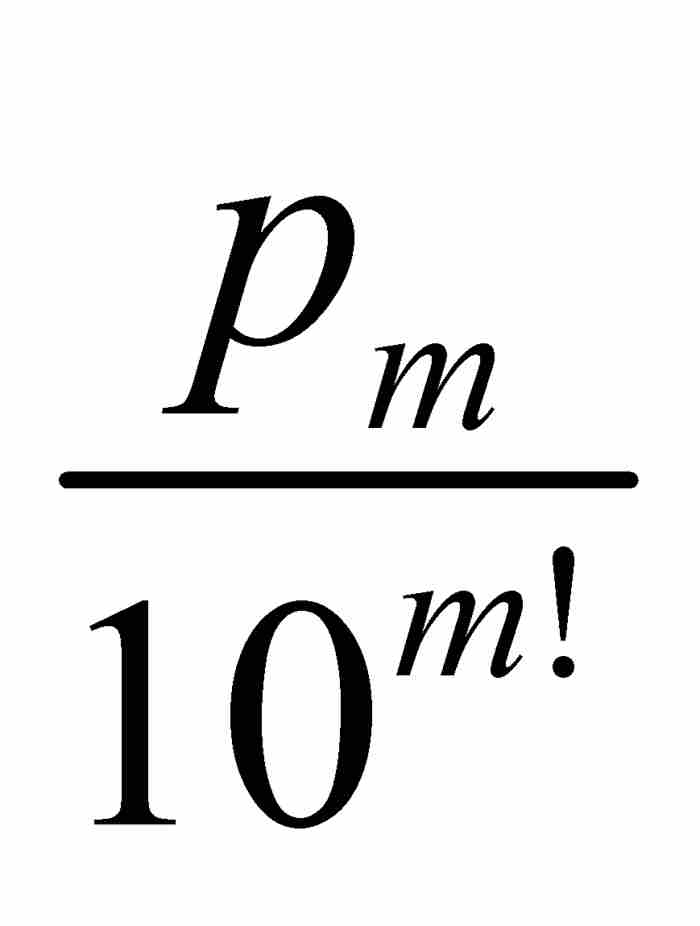当然是有理数。
把这个数同x0比较，我们看出
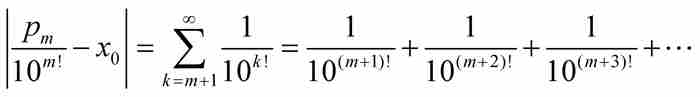
由归纳法证实，对于任何自然数r≥1，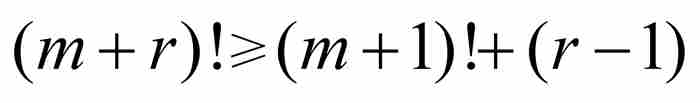
成立，所以有
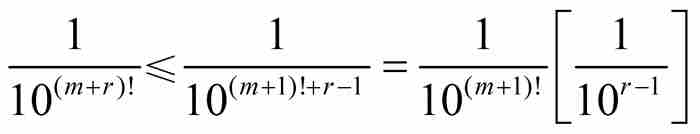。结果得到
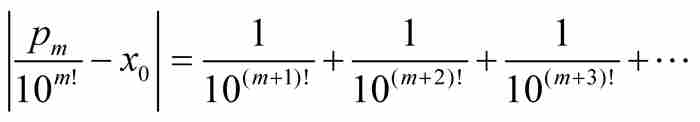
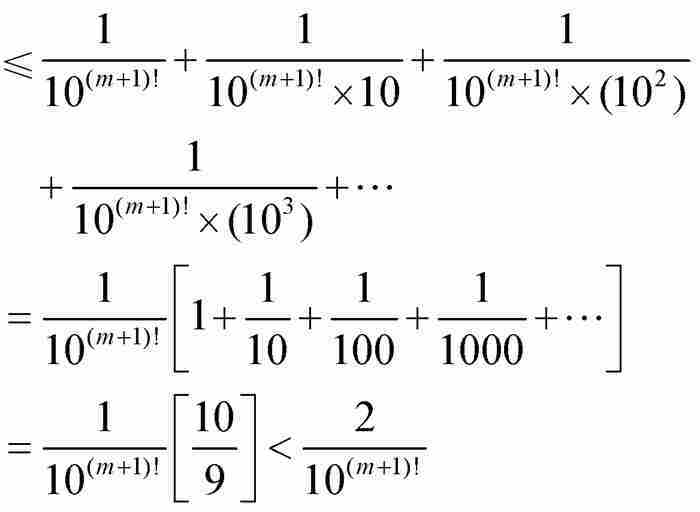
（8）
这样立即导致一个矛盾，因为
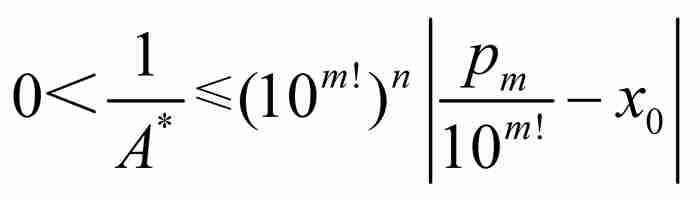（由式（7））
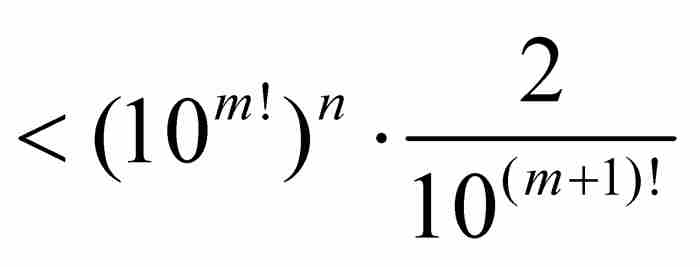（由式（8））
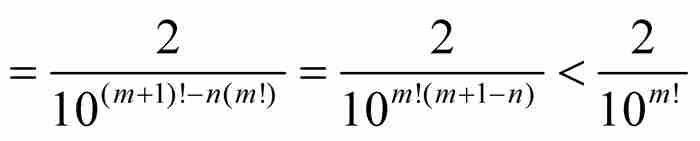
其中最后一步推导是由于m > n蕴含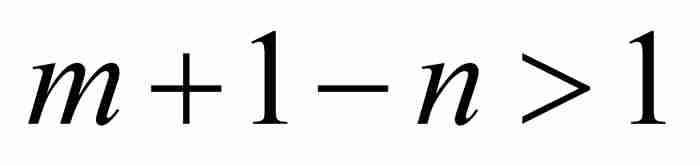
。
这一长串不等式表明，就上面引入的A*的值而言，对于所有m > n，我们有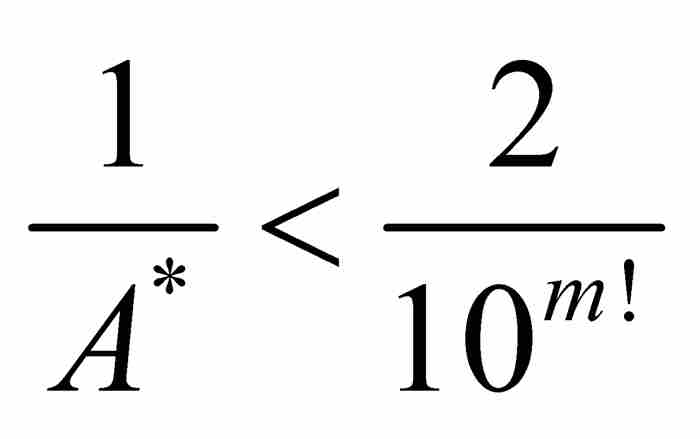
，或者简单地说，对于所有m > n，有2 A* > 10m!。这样一个不等式是荒谬的，因为2 A*是一个固定的数，而10m!当m增大时趋向无穷大。刘维尔（最终）导出一个矛盾。
至此，可能需要略微提醒一下读者出现了什么矛盾。已经假定无理数x0是一个代数数。然而，最终得到的却是另外一种结果，所以只有一种可能：x0必定是超越数。这样一个数的存在，就是约瑟夫·刘维尔试图证明的结论。
刘维尔在1851年发表的一篇文章中指出，尽管许多人推测超越数的存在，“我不相信已经给出过任何证明”。2 如今，终于有了一个证明。
2 J. Liouville, “Sur des classes très-étendues de quantités don't la valeur n'est ni algébrique, ni même réductible à des irrationnelles algébriques”, Journal de mathématiques pures et appliqués, vol. 16 (1851), p. 140。
说来奇怪，对于取得的这个成就，刘维尔认为还不能算是完全成功，因为他的初衷是希望证明e是一个超越数。3 像刘维尔所做的那样，构造一个数，然后证明它是超越数，这是一回事；而对于“已经存在的”如e那样的数，证明它是超越数，则是另一回事。对于这一点，Eric Temple Bell以其特有的鉴别力作出下面的评论：
证明一个特定的猜测，如像e或π是超越数或者不是超越数，同构造一类无穷的超越数相比，是困难得多的问题：……在这种情况下，被猜测的数是主导者，而数学家只能听命于它。4
3 Joseph Liouville 1809—1882: Master of Pure and Applied Mathematics (Springer-Verlag, 1990), pp. 79-81。
4 Eric Temple Bell, Men of Mathematics, Simon & Schuster, 1937, p. 463。
我们姑且可以这样说，刘维尔证明了过去无人关心的一个数的超越性，但是对于无处不在的常数e未能给出同样的证明，而这个数的超越性又是使数学家们魂牵梦绕的。超越数是在刘维尔之前的先躯们徒劳地寻找了一百年的东西，当他找到超越数后，如果仍然对他贴上失败的标签，无疑是荒唐可笑的。
刘维尔最初提出的目标很快将由他的继承者们实现。在1873年，查尔斯·埃尔米特（1822—1901）证明了e确实是一个超越数。九年之后，费尔登兰德·林德曼（1852—1939）对 π 证明了同样的结果。众所周知，林德曼曾经证实用圆规和直尺求圆的面积是不可能的，这是古希腊人提出的著名的“化圆为方”问题，历经几千年而非几十年或几百年不得其解。5 在埃尔米特和林德曼的结果中，包含着令人叹为观止的推理步骤，而这种推理是建立在刘维尔的开拓性研究工作之上的。
5 例如，参见William Dunham, Journey through Genius, Wiley, 1990, pp. 24 -26中的讨论。
时至今日，确定某个给定的数是不是超越数，在数学中仍然属于最困难的问题之列。在这方面已经取得了很大进展，很多重要的定理已经获得证明；然而，据我们了解，仍然留下大量的盲区。在已经得到的巨大成就中，我们不能不提出阿什波维奇·盖尔芳德（1906—1968）在1934年的证明，其中他一举证实了一族完整的超越数。他证明，如果a是一个不同于0或1的代数数，而b是一个无理数代数数，那么ab必定是超越数。这个深奥的结果，保证例如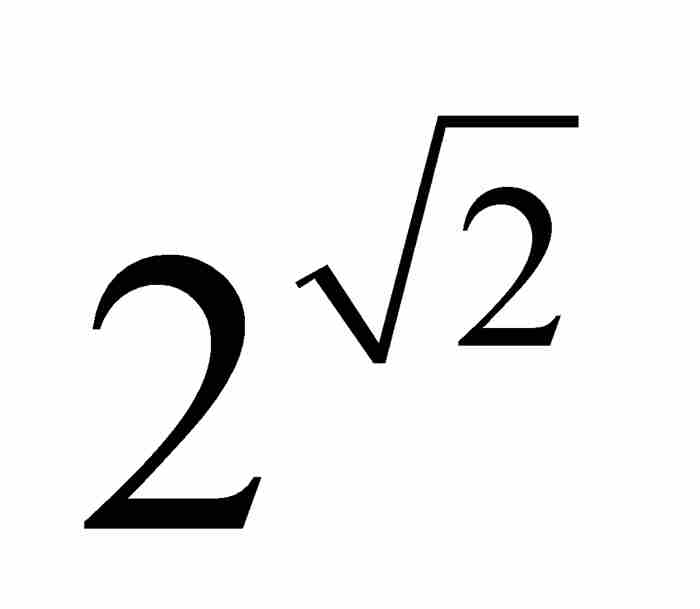
或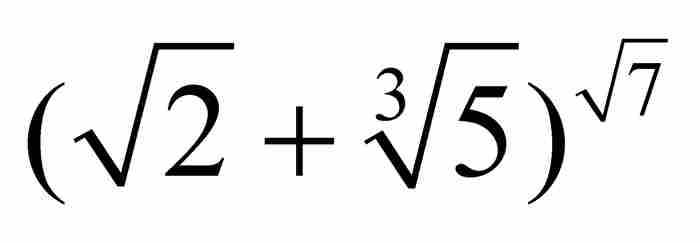
这样的数是超越数。如今已经知道，在超越数候选者之列的还有eπ，ln(2)和sin(1)。
然而，直到写作本书时，像 πe，ee和 ππ这样一些看似“简单的”数的性质尚有待证实。更为严重的是，尽管数学家们对 π + e和 π × e是超越数深信不疑，但是尚无人给出实际证明。6 我们再重复一遍：证明一个数的超越性是非常非常困难的。
6 Andrei Shidlovskii, Transcendental Numbers, de Gruyter, 1989, p. 442。
回到本章的主题，我们看出，到19世纪中期数学家们已经走了多远。刘维尔在处理不等式时表现出的学术才华以及他在如何攻克如此困难的问题方面的广阔视野，的确是令人难忘的。分析学已经步入它的成熟期。
在第11章将要证明关于实数完备性的一个里程碑式的定理，刘维尔这里的证明将同那个定理的证明形成鲜明的对照。在那里我们将会看到格奥尔格·康托尔如何找到一条明显的捷径，仅做少量的工作就得到刘维尔的结论。康托尔以这种方式改变了数学分析的方向。刘维尔和康托尔的相互影响将是一笔巨大财富，昭示我们如何使数学的活力延续下去。
不过，暂时不得不把康托尔的工作搁置一下。我们的下一个目标是展现19世纪分析学所追求的严格性的终点：卡尔·魏尔斯特拉斯的数学以及分析学中最著名的反例。