第3章 伯努利兄弟
04-13Ctrl+D 收藏本站

通常,一场科学革命不单是需要一位奠基的天才。它往往也需要一位组织天才,去确立科学中的核心思想,对它的产物去粗取精,去伪存真,并使之能为大众理解。一位卓越的建筑设计师可以设计出一幅宏伟的蓝图,但是这份蓝图终究需要一支建筑队伍将其变成一座大厦。
如果说牛顿和莱布尼茨是微积分的建筑设计师,那么正是雅各布·伯努利和约翰·伯努利所做的大量工作,才把微积分建立成今天我们所知的这门学科。这兄弟二人阅读了莱布尼茨从1684年到1686年发表的最早论文,他们发现自己如临决斗前那样兴奋。他们抓住云山雾罩般的阐述,充实它的细节,然后通过与莱布尼茨的交流以及兄弟彼此之间的交流,完善了统一性、条理性和术语。例如,“积分”一词正是雅各布给出的。1 在他们手中,微积分变成当今学生易于接受的形式,即具有基本的求导法则、积分方法和初等微分方程的解法。
1 Howard Eves, An Introduction to the History of Mathematics, 5th Ed., Saunders College Publishing, 1983, p. 322。
虽然同属优秀的数学家,但是伯努利兄弟二人的个人表现完全可以用“不得体”来形容。尤其是约翰,在莱布尼茨与牛顿关于微积分发明权之争中充当了好斗的角色,像莱布尼茨的牛头犬一样,忠实地站在他所尊奉为英雄的“大名鼎鼎的莱布尼茨”一边,甚至声称牛顿不仅没有发明微积分,而且从来没有完全理解它。2 这当然是对历史上最杰出的一个数学家的粗野无端的攻击。
2 Richard S. Westfall, Never at Rest, Cambridge University Press, 1980, pp. 741-743。
非常不幸,由于家庭不和睦,雅各布和约翰也以相互争斗为乐。例如,哥哥雅各布称弟弟约翰为“我的学生”,即使是在这个学生的才干已经明显和他相当的时候也是这样。同样,约翰在事隔多年后还在津津乐道地谈论如何在一个晚上解决了困扰雅各布将近一年的一个问题。3
3 Morris Kline, Mathematical Thought from Ancient to Modern Times, Oxford University Press, 1972, p. 473。
尽管他们具有难以相处的执拗天性,但是,伯努利兄弟还是在数学史上写下了浓墨重彩的篇章。雅各布除了在微积分上的贡献以外,还著有《猜度术》一书,在1713年(他去世后)出版。这本书是概率论的经典之作,书中给出大数定律的证明,为了纪念他,人们往往把这个基本结果称为“伯努利定理”。4 至于约翰,他是世界上第一本微积分教科书的捉刀人。这件事情起于一项协议,按照协议约翰给法国贵族马奎斯·德·洛必达(1661—1704)提供微积分课材料,获取报酬。洛必达随后在1696年整理出版了这些材料,书名为《用于了解曲线的无穷小分析》。在这本书里首次出现“洛必达法则”,虽然同这本书一样,这个法则实际上是约翰·伯努利发现的,但是这个名称在微分学中从此就固定下来。5 在书的前言里,洛必达表达了对伯努利和莱布尼茨的感谢,他写道:“我无偿地使用了他们的发现,所以只要他们愿意,我真诚地把他们要求拥有的任何东西归还他们。”6
4 Jakob Bernoulli, Ars conjectandi (Reprint), Impression anastaltigue, Culture et Civilisation, Bruxelles, 1968。
5 L'Hospital, Analyse des infiniment petits (Reprint), ACL-Editions, Paris, 1988, pp.145-146。
6 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p. 312。
性情暴躁的约翰当然不满足于这种表示,他确实声明这个法则是他发明的,而在几年后,他抱怨洛必达用金钱换取他人的才智。当然正如数学史家Dirk Struik所说,是伯努利自己(实际)促成了这起交易。他给我们的简单的劝告是“就让善良的马奎斯持有他的典雅的法则吧,他支付费用了”。7 为避免再次失去荣誉,约翰写了一篇关于积分学的内容广泛的论文,在1742年用自己的署名发表。8
7 Dirk Struik, “The origin of L'Hospital's rule,” Mathematics Teacher, Vol. 56 (1963), p. 260。
8 Johannis Bernoulli, Opera omnia, vol. 3, Georg Olms, Hildesheim, 1968, pp. 385-563。
为更清楚了解伯努利兄弟二人在数学上的成就,我们有选择地介绍他们的成果。首先从雅各布的调和级数的发散证明开始,然后考察他对一些奇异收敛级数的处理,最后介绍约翰对他所谓 “指数微积分”的贡献。
雅各布和调和级数
像在他之前的牛顿和莱布尼茨以及许多后来的数学家一样,雅各布·伯努利认为无穷级数是进入分析学的必由之路。这一点从1689年他所写的专题论文《论无穷级数及其有限和》中可以明显看出。这篇文章是对无穷级数的最高水平的讨论,因为无穷级数在临近17世纪末才被人们了解。1 雅各布考察了一类相似的级数,例如等比级数、二项式级数、反正切级数和对数级数,以及某些以前从未讨论过的级数。在本章,我们考察从《论无穷级数及其有限和》中节录的两段文字,第一段专门讨论调和级数的奇异特性。
1 “论无穷级数及其有限和”是雅各布·贝努利《猜度术》一书的附录,参见[4],pp. 241-306。
在1689年之前很久,有人已经发现级数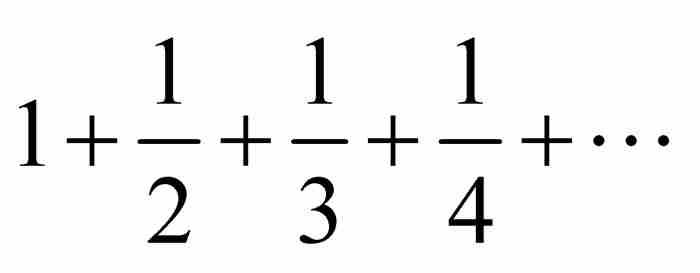 发散到无穷大。在大多数现代教科书中可以找到尼科尔·奥雷姆(大约1323—1382)发现的证明,以及彼得罗·门戈里(1625—1686)提出的另一种证明。2 莱布尼茨也许并不了解这两位先驱者的工作,在他早年在巴黎任职期间发现这个级数是发散的,用他的话说是
发散到无穷大。在大多数现代教科书中可以找到尼科尔·奥雷姆(大约1323—1382)发现的证明,以及彼得罗·门戈里(1625—1686)提出的另一种证明。2 莱布尼茨也许并不了解这两位先驱者的工作,在他早年在巴黎任职期间发现这个级数是发散的,用他的话说是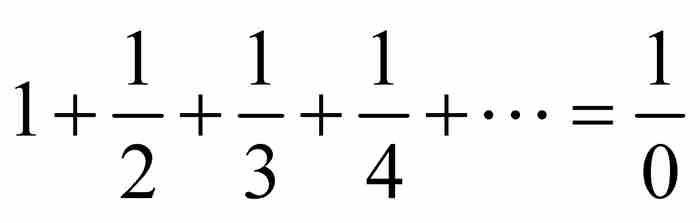 ,并告诉他的英国同行,而从他们那里获悉,又有人捷足先登了。3
,并告诉他的英国同行,而从他们那里获悉,又有人捷足先登了。3
2 参见William Dunham, Journey through Genius, Wiley, 1990, pp. 202-205。
3 Joseph E. Hofmann, Leibniz in Paris: 1672-1676, Cambridge Univesity Press, 1974, p. 33。
所以,调和级数的发散已不再是新闻。但是,我们通过下面另外一种方法得到同样的结果,可以增长见识,更不必说其中的多样性的魅力了。雅各布·伯努利的发散性证明就是与他的前辈们的证明迥然不同的这样一种方法。
等比数列和等差数列在他那个时代如日中天,他首先从对比这两类数列开始。他将前一种数列描述为A, B, C, D, …,其中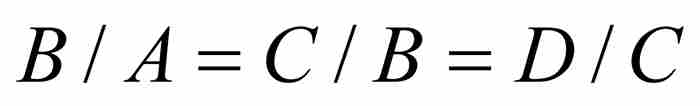 ,等等,例如,2, 1, 1/2, 1/4,…。他将后一种的数列,写成A, B, C, D,…的形式,其中
,等等,例如,2, 1, 1/2, 1/4,…。他将后一种的数列,写成A, B, C, D,…的形式,其中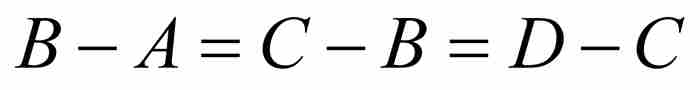 ,等等;一个例子就是2, 5, 8, 11,…。当然,现代的书写习惯是强调等比数列的公比(r)和等差数列的公差(d),因此我们将等比数列写成
,等等;一个例子就是2, 5, 8, 11,…。当然,现代的书写习惯是强调等比数列的公比(r)和等差数列的公差(d),因此我们将等比数列写成 ,
,  ,
, 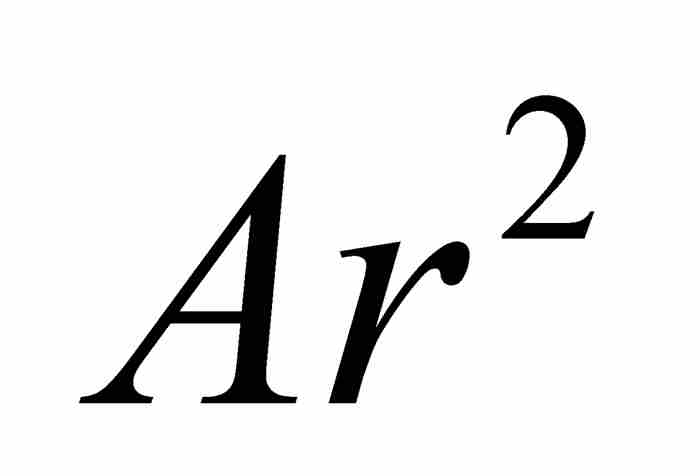 ,
, 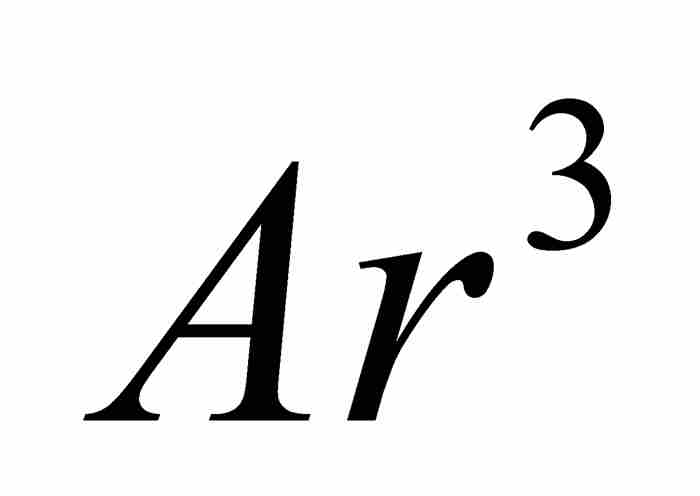 , …,而将等差数列写成
, …,而将等差数列写成 ,
, 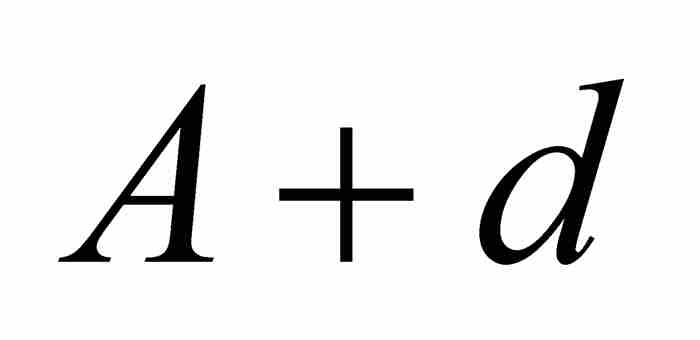 ,
, 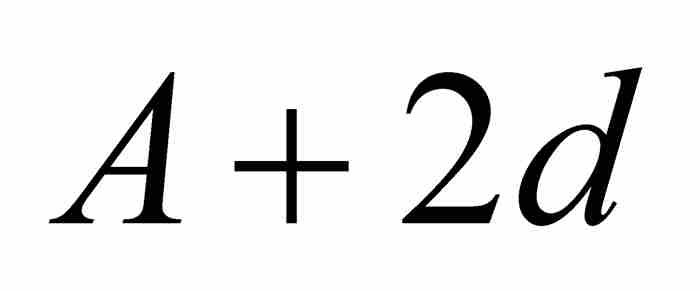 ,
, 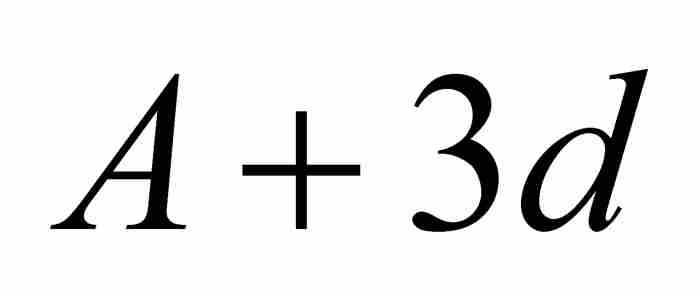 , …。
, …。
作为雅各布的《论无穷级数及其有限和》的第4个命题,他证明了关于前两项相同的正数项等比数列和等差数列的一个引理。
定理 如果A, B, C,…, D, E是公比为r>1的正数项的等比数列,而A, B, F,…, G, H也是从A和B开始的正数项的等差数列,那么,等比数列中其余每一项都大于对应的等差数列中的相应项。
证明 使用现代的记号,我们将等比数列表示为 ,
,  ,
, 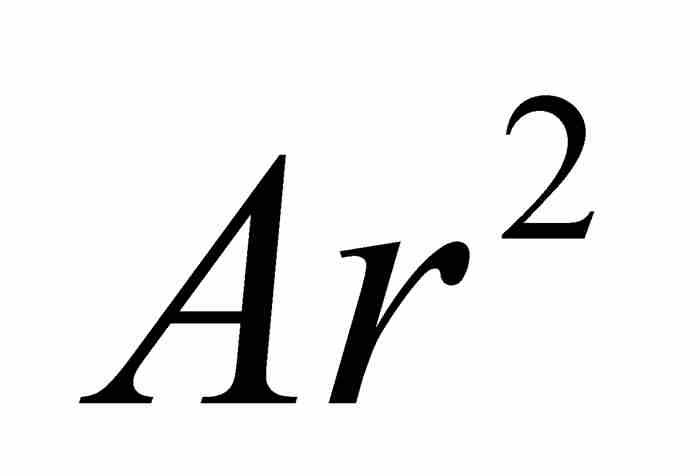 ,
, 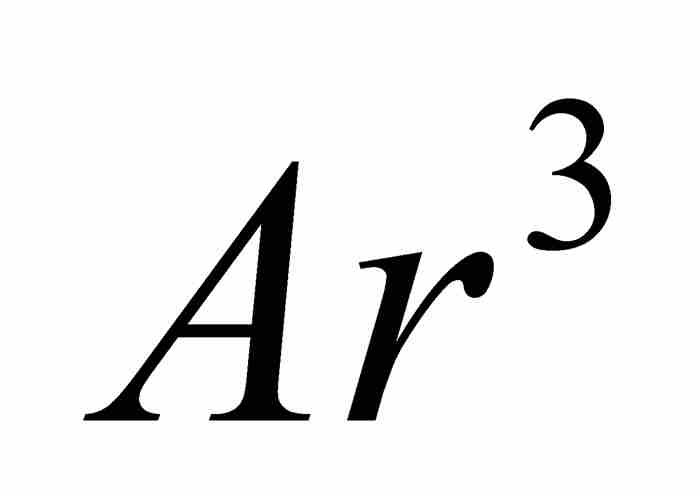 , … ,而将等差数列表示为
, … ,而将等差数列表示为 ,
, 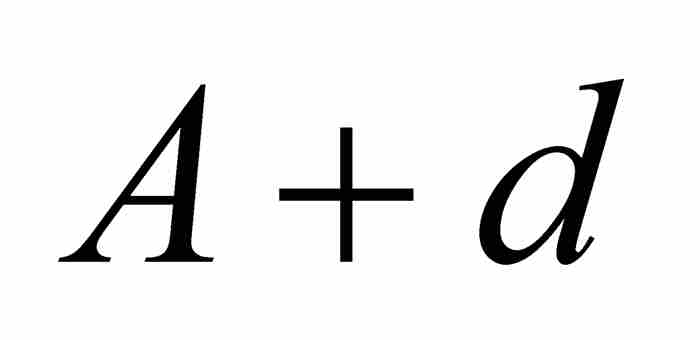 ,
, 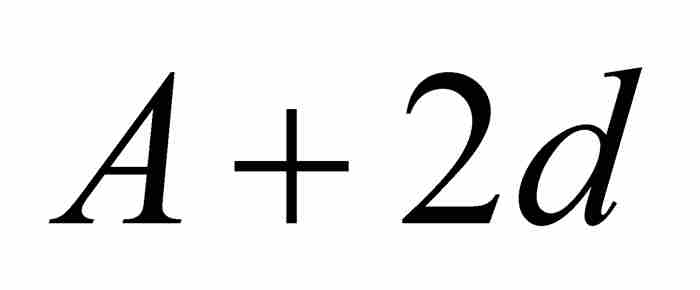 ,
, 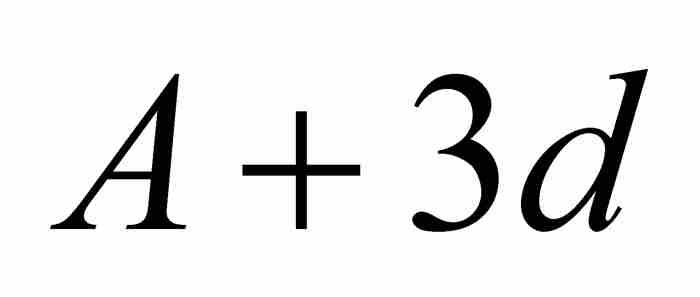 , …。根据假设,可知
, …。根据假设,可知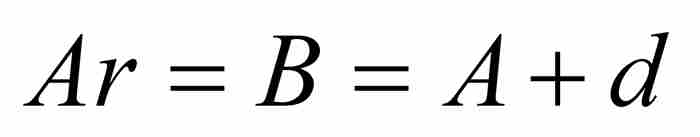 。由于
。由于 ,我们有
,我们有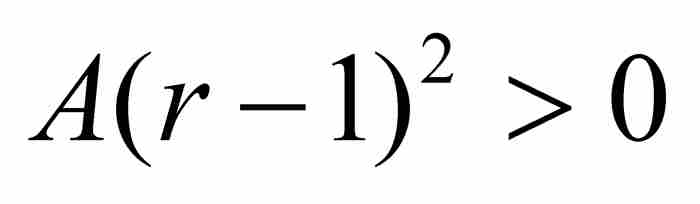 ,展开得到
,展开得到
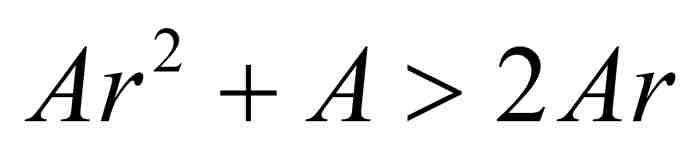
或者简化成
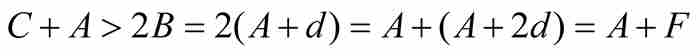
因此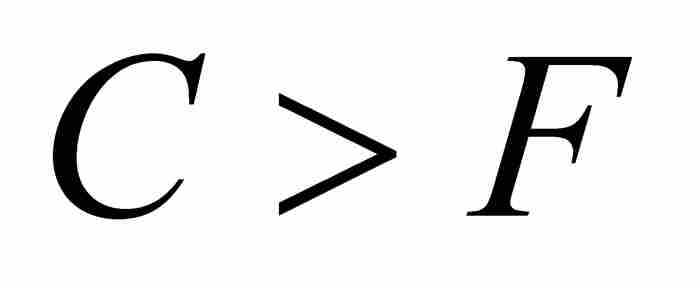 ,这就是说,如定理所述,等比数列的第3项大于等差数列的第3项。这个证明,可以重复到第4项、第5项以及此后的任何项。
,这就是说,如定理所述,等比数列的第3项大于等差数列的第3项。这个证明,可以重复到第4项、第5项以及此后的任何项。
在几个命题之后,雅各布证明了在描述方式上带有17世纪风格的下述结果。
定理 在任意有限项等比数列A, B, C, …, D, E中,第1项与第2项的比,等于除最后一项外所有项的和与除第1项外所有项的和的比。
证明 一旦我们掌握了不熟悉的数学语言,这是就很容易证明的,因为
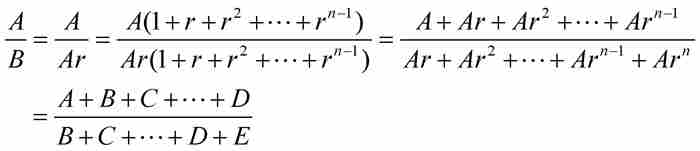
接下来雅各布求有限项等比数列的和。令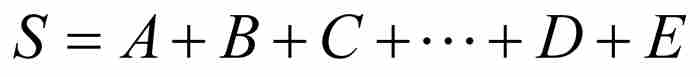 为待求的和,他应用上述结果得到
为待求的和,他应用上述结果得到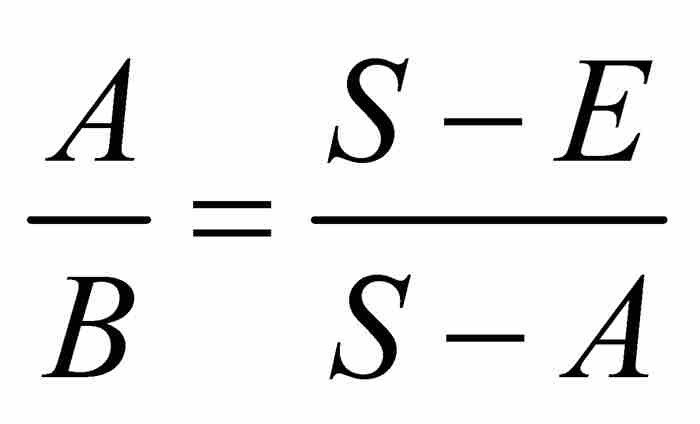 ,求解得
,求解得
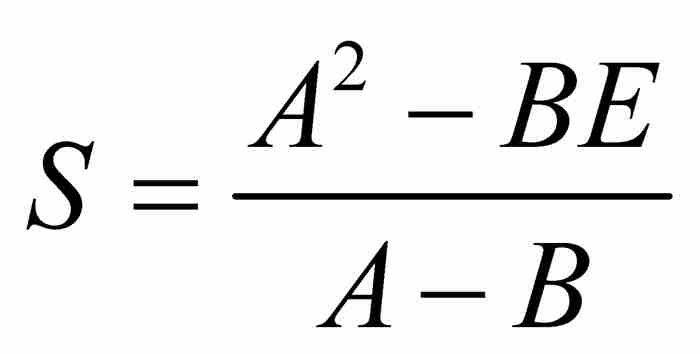 (1)
(1)
注意式(1)用到了有限等比数列的第1项(A)、第2项(B)和最后一项(E)。这与我们今天看到的标准求和公式
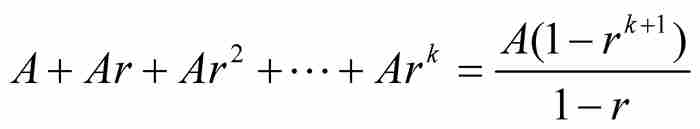
不同,这个公式利用的是第1项、项数和公比。
以这些预备知识做铺垫,现在我们可以看看雅各布对调和级数进行的分析。此项分析在《论无穷级数及其有限和》一文中紧接在约翰的级数发散证明之后。4 将弟弟的成果包含在他的论文中也许显得异乎寻常地慷慨,但是雅各布发起了挑战,给出自己的另一个证明。用他的话说,目标是证明“无穷调和级数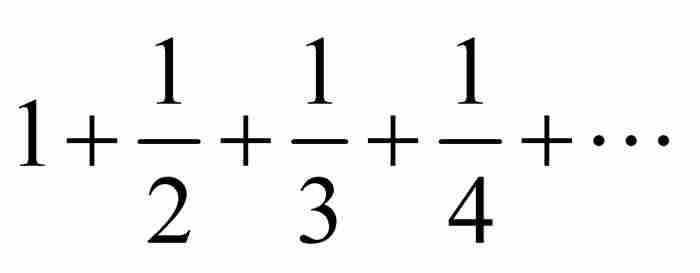 的和超过任意给定的数。因此,它的和为无穷大”。5
的和超过任意给定的数。因此,它的和为无穷大”。5
4 Jakob Bernoulli, Ars conjectandi, p. 250。
5 Jakob Bernoulli, Ars conjectandi, p. 251。
定理 调和级数发散。
证明 选择任意自然数N,雅各布首先试图从调和级数中去除从第1项开始的相继若干项,这些项的和大于或等于1。他再从剩下的项中,去除和等于或大于1的相继若干项。按这种方式进行下去,直到N次把这样的有限项去除,使整个调和级数之和减少的值至少为N。由于N是任意的自然数,所以调和级数之和为无穷大。
倘若我们总是能去除和为1或更大的有限项,那么从雅各布的文章中几乎一字不差地抄录下来的这个论证步骤就是正确的。为完成证明,伯努利必须证明这的确是事实。于是,他假定情况相反,就是说,“如果在去除一些项后,剩余项之和不可能超过1,那么,令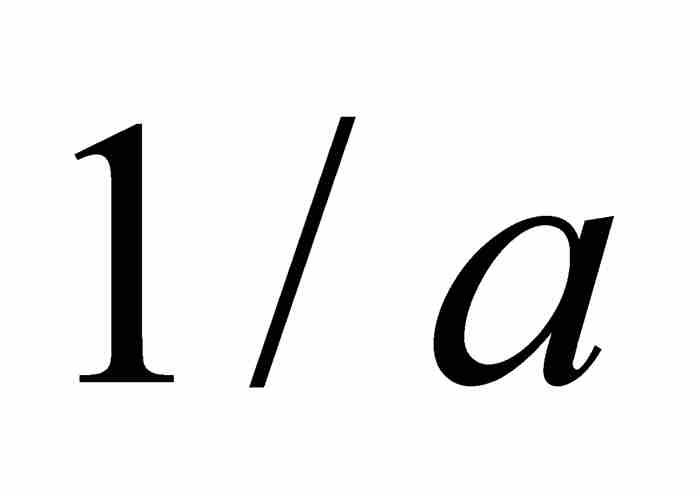 为最后一次去除有限项以后的第1项”。换句话说,为了引出矛盾,他假定不管达到多少项,
为最后一次去除有限项以后的第1项”。换句话说,为了引出矛盾,他假定不管达到多少项,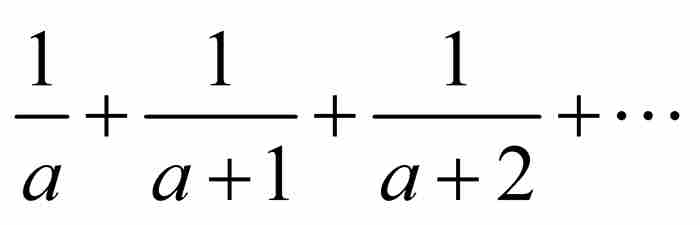 的和都小于1。但是这些分母
的和都小于1。但是这些分母 ,
, 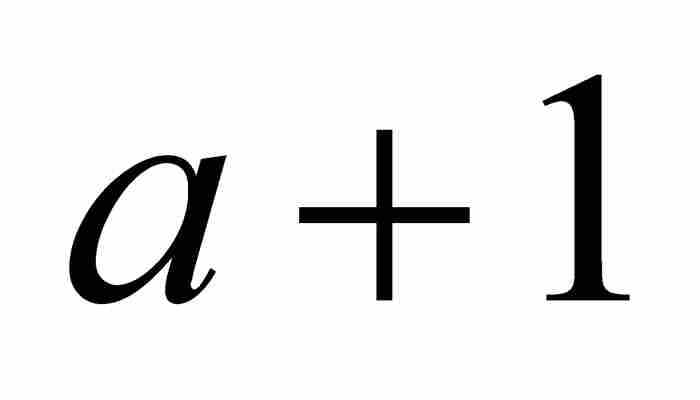 ,
, 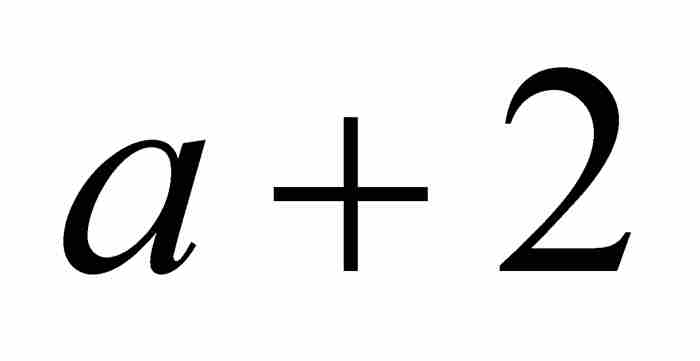 , …构成一个等差数列,因此雅各布引入与这个等差数列前两项相同的等比数列。就是说,他考虑等比数列
, …构成一个等差数列,因此雅各布引入与这个等差数列前两项相同的等比数列。就是说,他考虑等比数列 ,
, 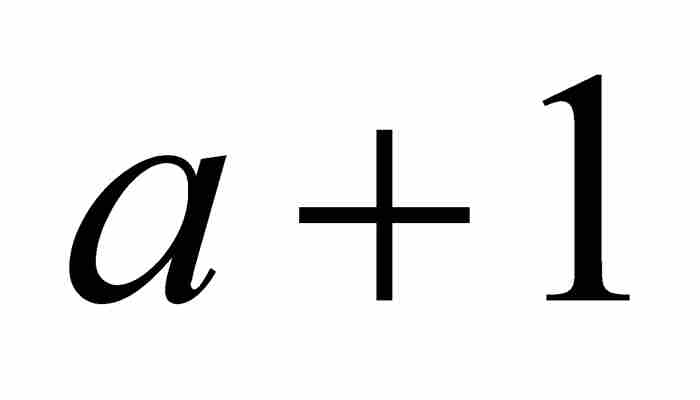 , C, D, …, K,其中他要求我们一直取到
, C, D, …, K,其中他要求我们一直取到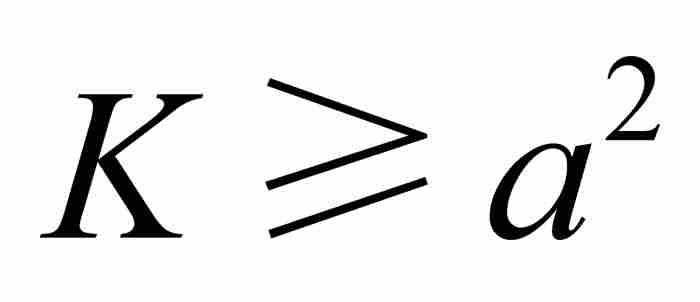 。这是可以做到的,因为数列的公比为
。这是可以做到的,因为数列的公比为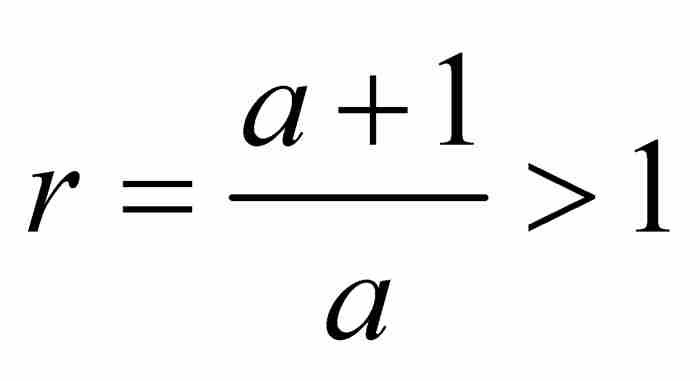 ,所以其项可以随意地增大。
,所以其项可以随意地增大。
如前所见,雅各布知道等比数列的每一项都大于对应的等差数列的相应项,因此,他取倒数,推出
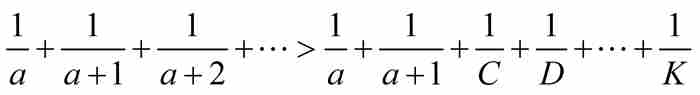
其中不等式左边具有的(有限)项数同右边的项数相等。雅各布使用式(1)计算这个等比数列的和,其中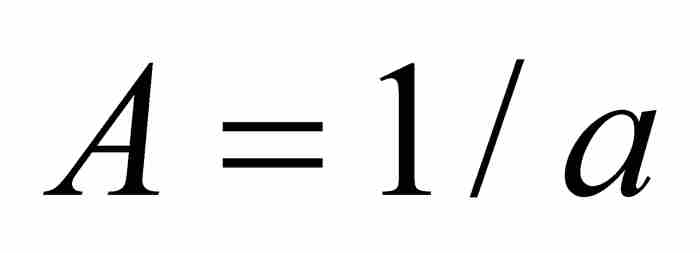 ,
,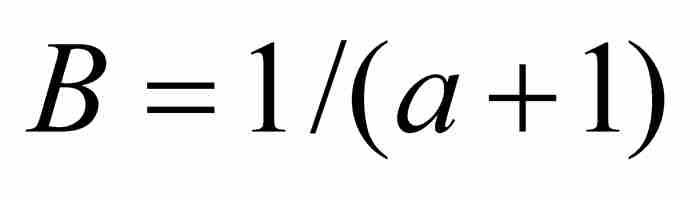 ,而
,而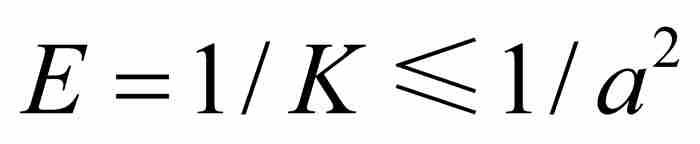 ,得到
,得到
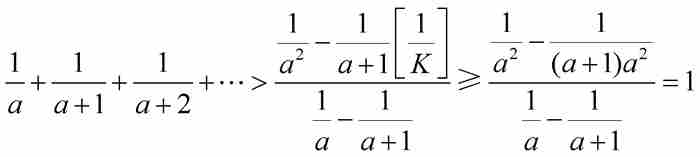
这与他最初的假设矛盾。通过这种方式,雅各布断定,从调和级数的任何一项开始,其剩余部分的某个有限项的和必然超过1或者更大。
为了完成证明,他使用下面的方式重新组合调和级数:
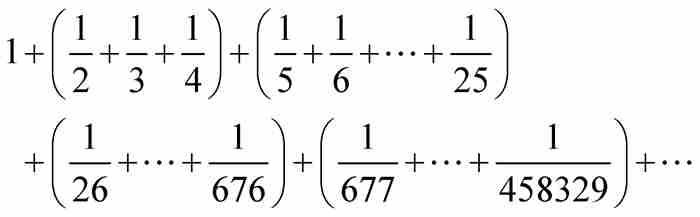
其中每个括号中的表达式都超过1。因此,所得的和可以比任何预先指定的数大,所以调和级数发散。
这是一个构思巧妙的证明。雅各布很清楚它的重要意义,他强调,“一个最后项趋近零的无穷级数的和也许是有限的,也许是无限的”。6自然,不会有现代数学家谈论无穷级数的“最后项”,但是雅各布的意图是清楚的:即使无穷级数的一般项缩小至零,也不足以保证级数收敛。调和级数就是一个极好的例子。雅各布·伯努利因此证明了这一点,今天大家依然采用这个证明。
6 Jakob Bernoulli, Ars conjectandi, p. 252。
雅各布和他的垛积级数
调和级数之所以被关注是因为它的不良特性,即发散性。受到同样关注的是具有有限和这种良好特性的无穷级数。雅各布从等比级数开始并巧妙地对其进行改变,计算了一些非同一般的级数的精确值。下面我们考察其中几个级数。
首先,他需要求无穷等比数列的和。如式(1)所示,伯努利使用公式
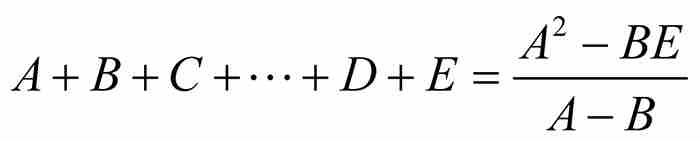
求出有限等比数列的和。他注意到一个必然结果,由正数构成的公比小于1的无穷等比数列的一般项必定趋近零。因此,他简单地令他的“最后”项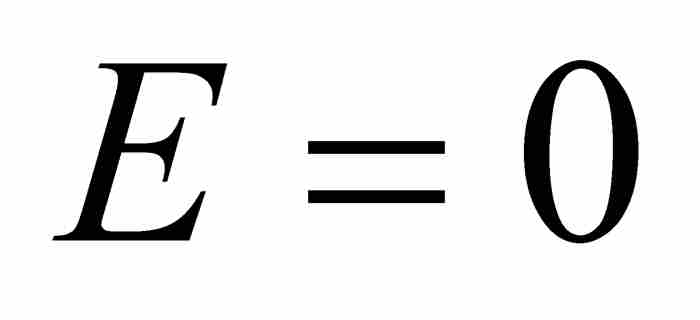 ,得到
,得到
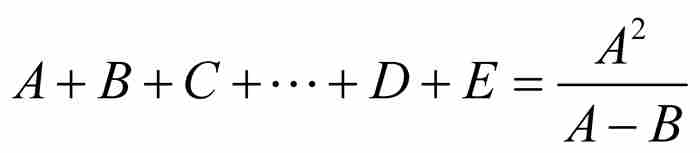 (2)
(2)
等差数列和等比数列并不是17世纪的数学家们唯一熟悉的数列形式。他们也熟悉“垛积数”,这是同某些几何形体(如三角形、棱锥体和立方体)相关的整数的家族。例如我们有三角形数1, 3, 6, 10, 15, …,这样命名是因为它们来源于图3-1所示的不断扩展的三角形中的点数。容易看出,第k个三角形数是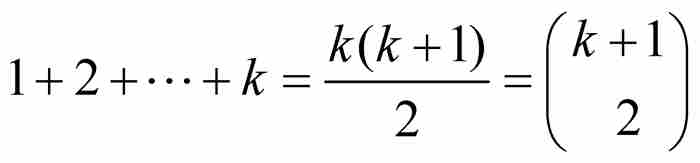 ,其中的二项式系数是在雅各布·伯努利之后才出现的记号。
,其中的二项式系数是在雅各布·伯努利之后才出现的记号。
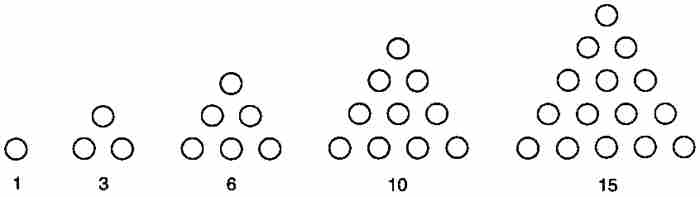
图 3-1
同样,棱锥体数是1, 4, 10, 20, 35, …,它们是以三角形为底的棱锥垛中弹丸的数目。可以证明,第k个棱锥体数是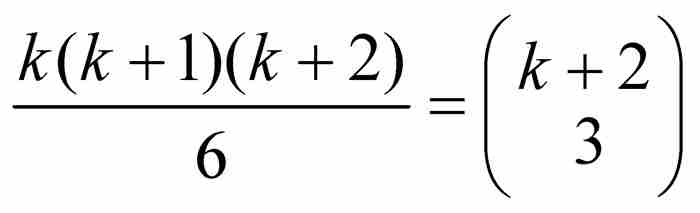 。自然,正方形数1, 4, 9, 16, 25, …和立方体数1, 8, 27, 64, 125, …同样有其几何意义。
。自然,正方形数1, 4, 9, 16, 25, …和立方体数1, 8, 27, 64, 125, …同样有其几何意义。
伯努利在这方面的研究兴趣表现为如下形式:他想求出无穷级数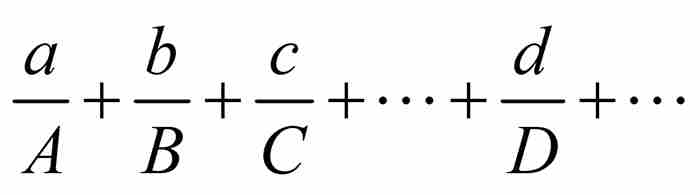 的精确和,其中,分子a, b, c, …, d, …是垛积数,而分母A, B, C, …, D, …构成等比数列。例如,他想要计算
的精确和,其中,分子a, b, c, …, d, …是垛积数,而分母A, B, C, …, D, …构成等比数列。例如,他想要计算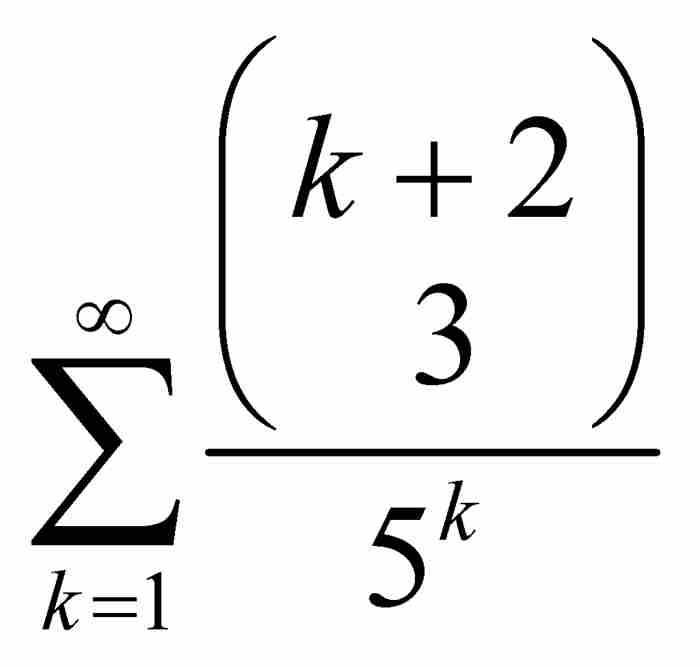 或者
或者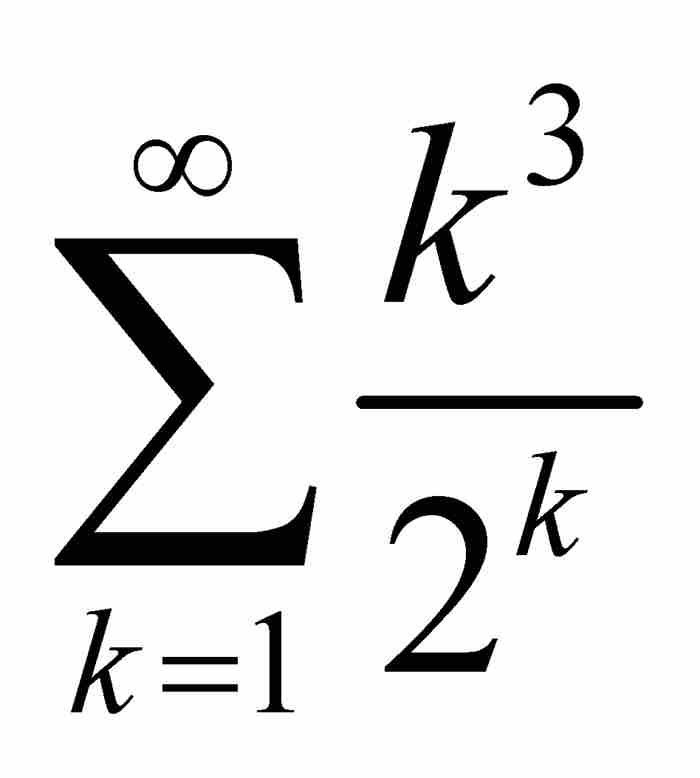 这样一些级数的和。当时,这种求和是极具挑战性的问题。
这样一些级数的和。当时,这种求和是极具挑战性的问题。
雅各布解决这类问题的办法是先解决简单问题,再解决复杂问题,在数学上,这始终是一种正确的策略。仿照他的论证过程,我们从以自然数为分子和等比数列为分母的无穷级数着手。1
1 Jakob Bernoulli, Ars conjectandi, pp. 246-249。
定理N 如果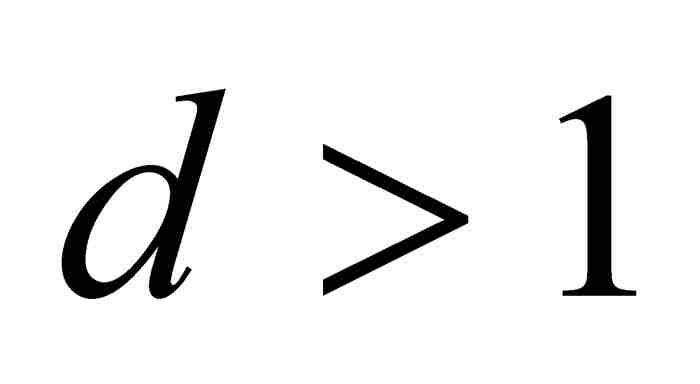 ,那么
,那么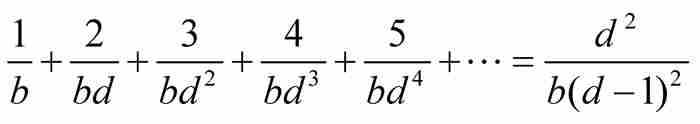 。
。
证明 雅各布令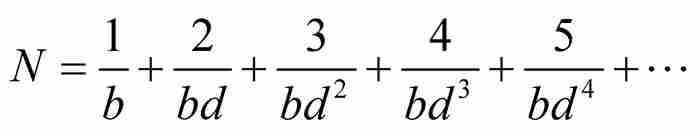 ,然后将其分解为一系列无穷等比数列,再利用式(2)对每个数列求和:
,然后将其分解为一系列无穷等比数列,再利用式(2)对每个数列求和:
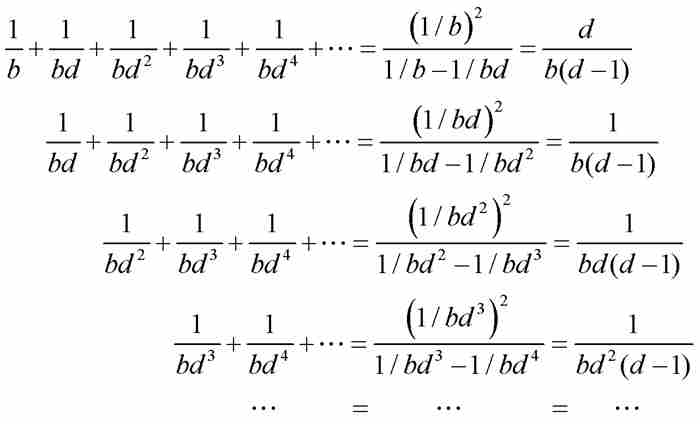
对上述等式按列相加,他求出
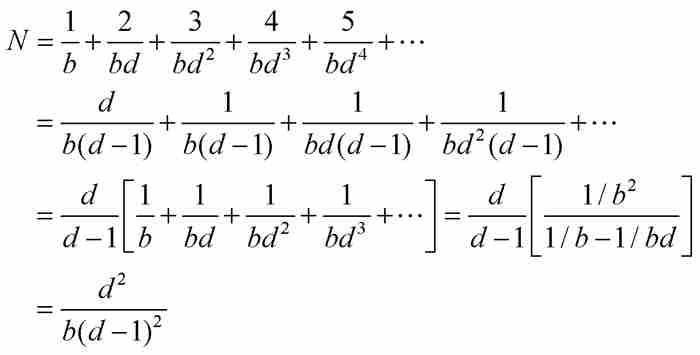
因为方括号中的无穷级数又是等比级数。
例如,当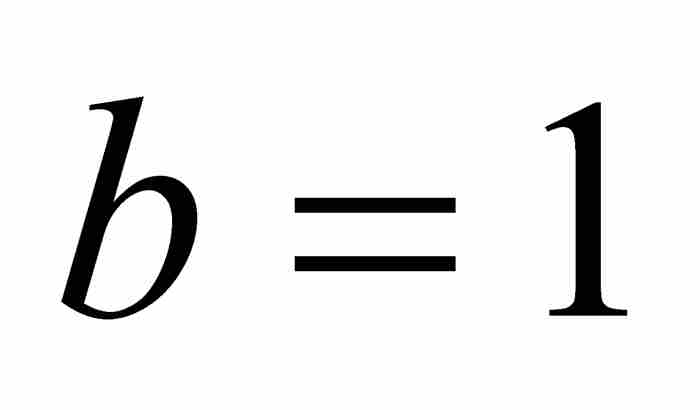 和
和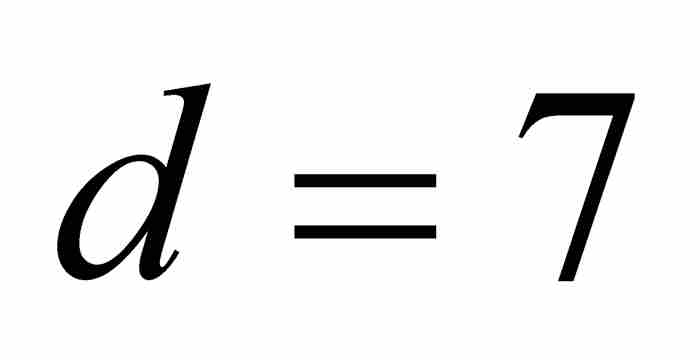 时,可得
时,可得 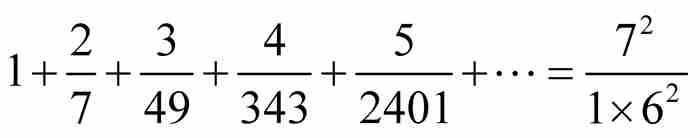
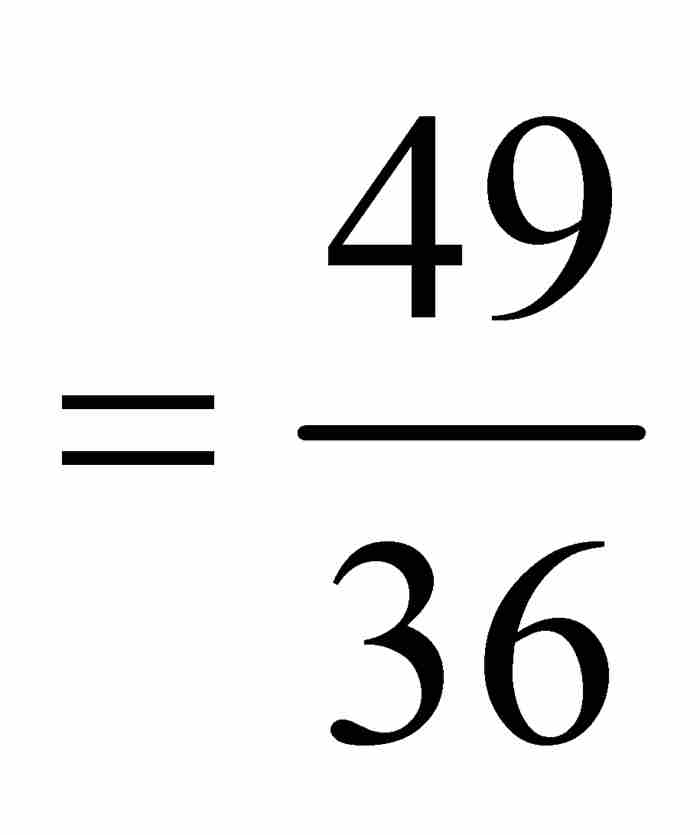 。
。
下一步,雅各布将分子换成三角形数。
定理T 如果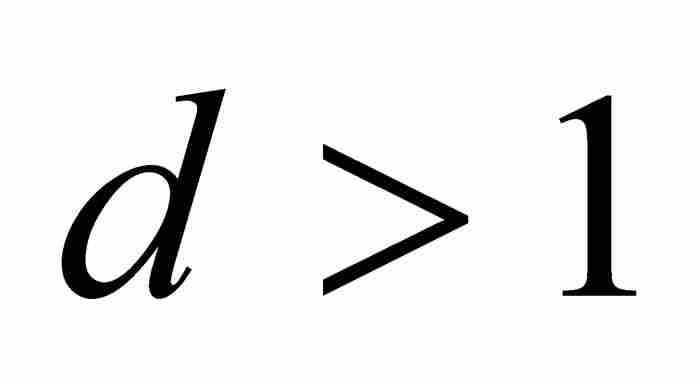 ,那么
,那么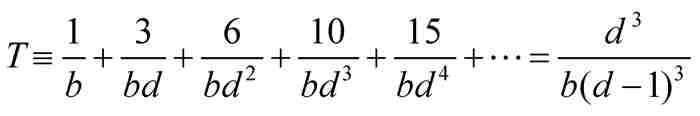 。
。
证明 窍门是将T分解成一系列等比级数,并且利用第k个三角形数为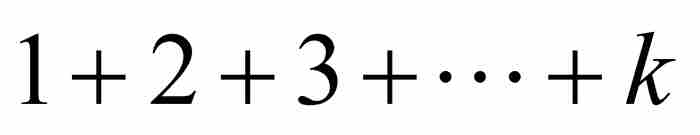 这个事实:
这个事实:
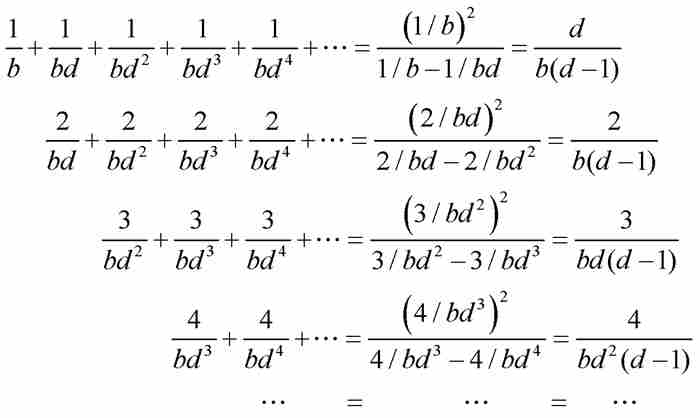
对上述等式按列相加,得到
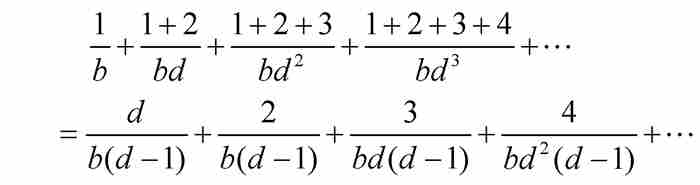
换句话说,由定理N可得
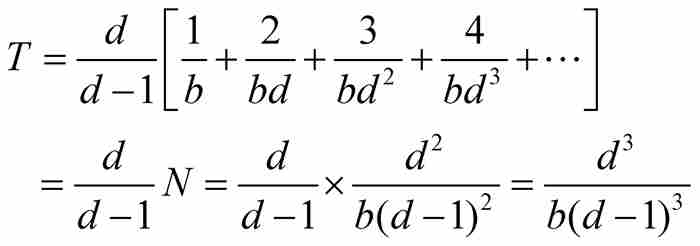
例如,当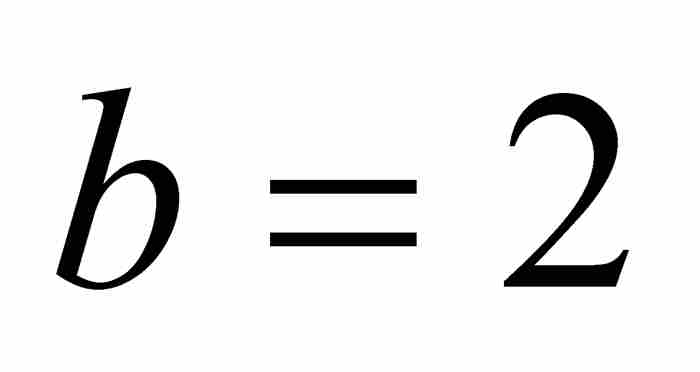 和
和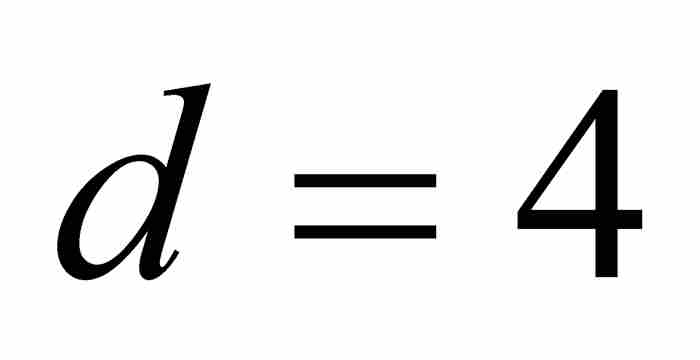 时,有
时,有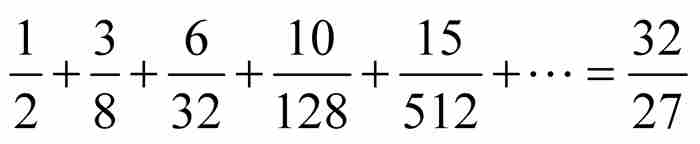 。
。
接下来雅各布考虑分子为棱锥体数的情况。
定理P 如果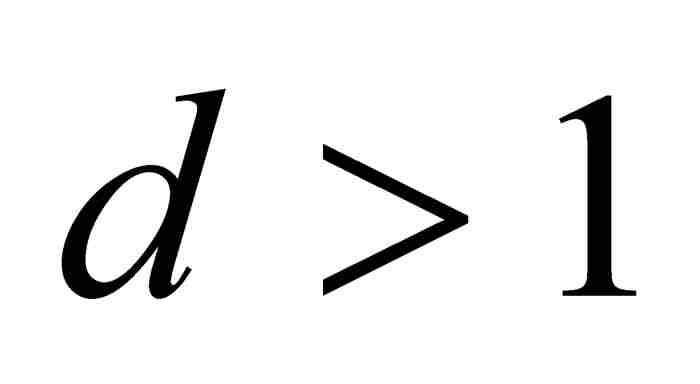 ,那么
,那么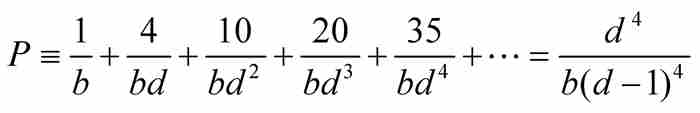 。
。
证明 这个证明很简单,因为
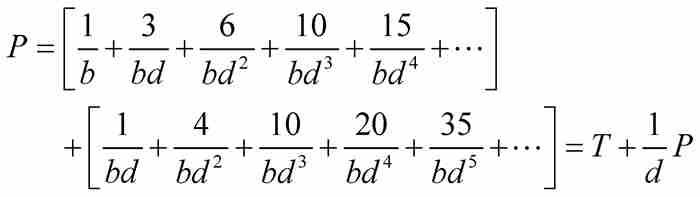
由于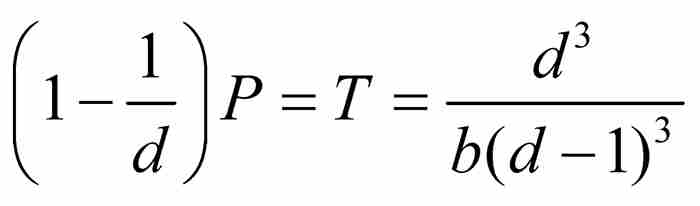 ,所以
,所以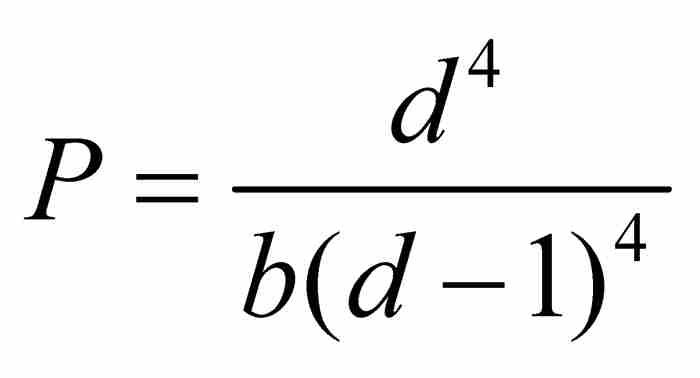 。
。
例如,当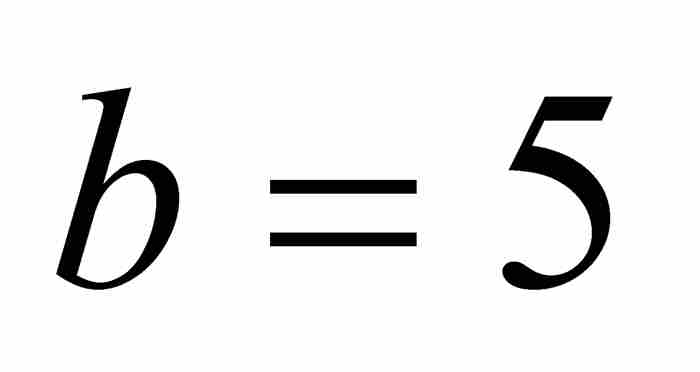 和
和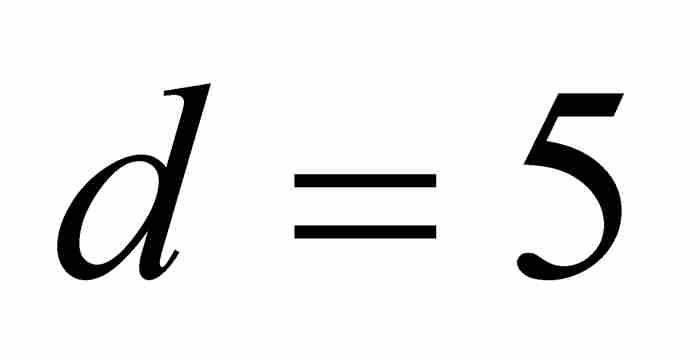 时,可得
时,可得
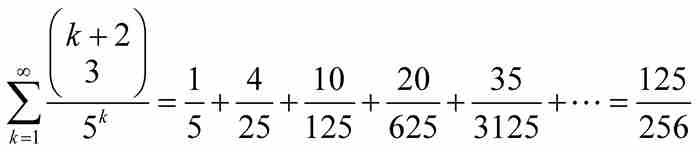
在《论无穷级数及其有限和》一文中这一部分的最后,雅各布讨论了以立方体数为分子和等比数列为分母的无穷级数。
定理C 如果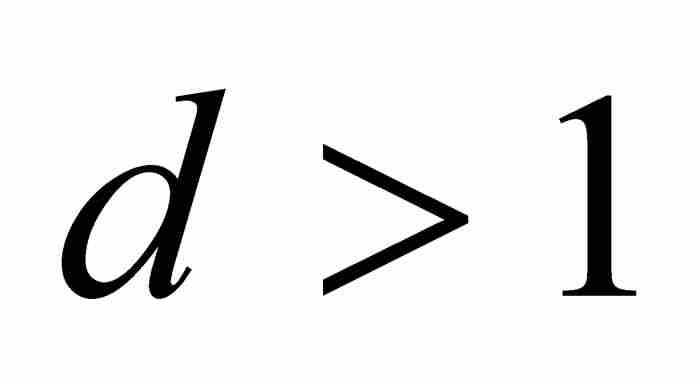 ,那么
,那么
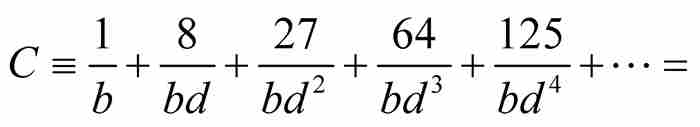
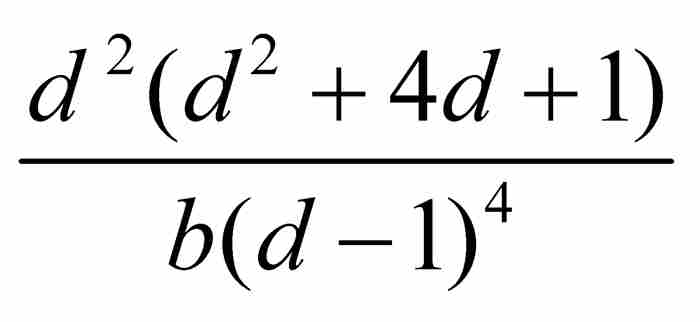
证明
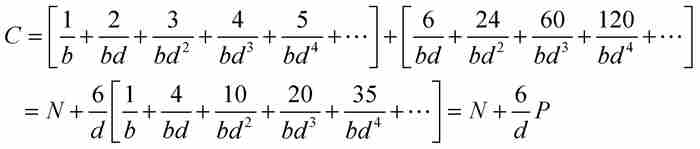
所以
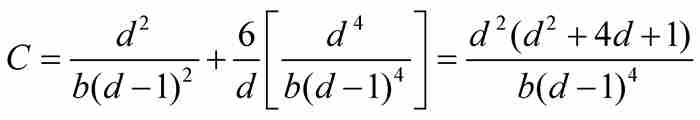
当雅各布令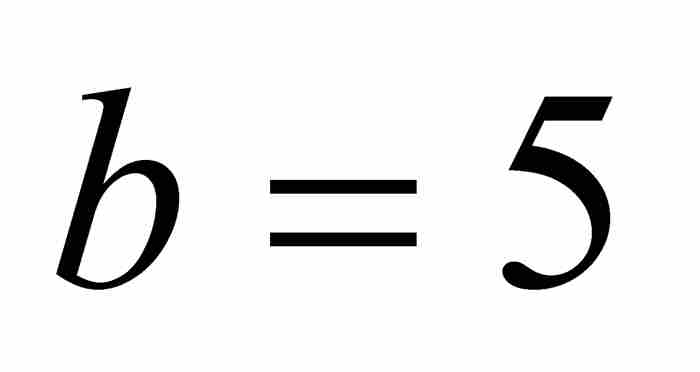 和
和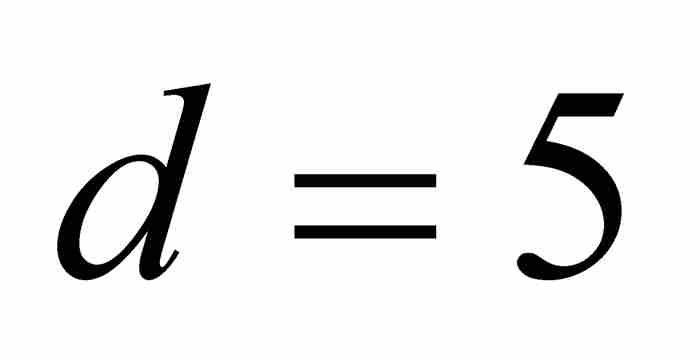 时,他得到精确的和:
时,他得到精确的和:
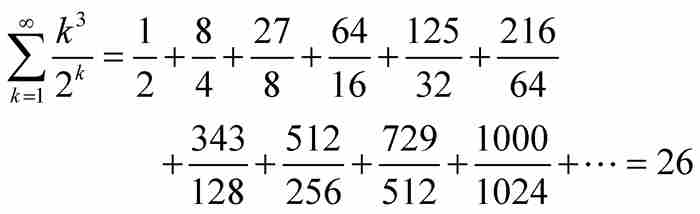
这是一个令人惊奇而又非直观的结果。
在取得这些成果之后,雅各布·伯努利也许开始感到无往而不胜了。倘若他当时真地怀有这种想法,很快也会转变态度的,因为由平方数的倒数构成的级数,即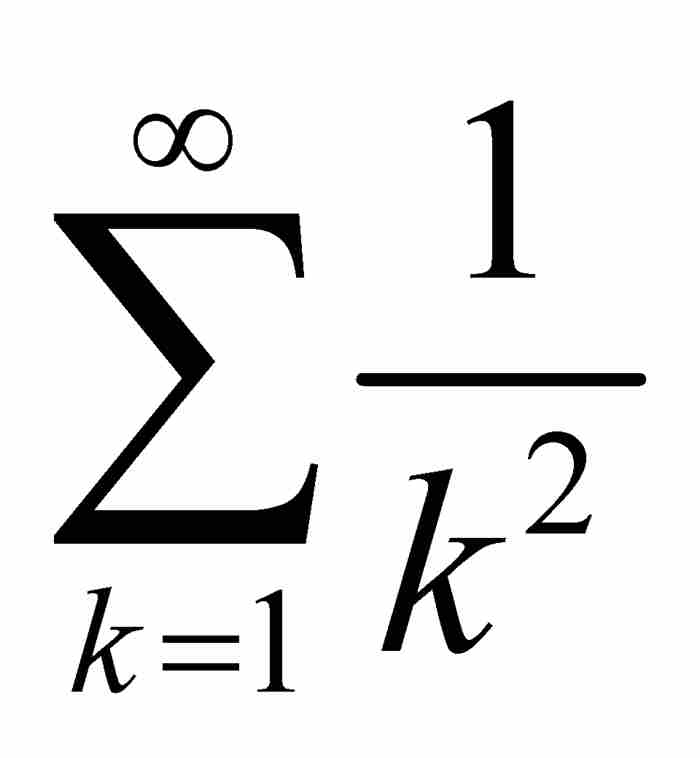 ,挡住了他的去路。他可以采用我们现在所知的比较检验法证明这个级数收敛于某个小于2的数,但是他未能求出这个数。雅各布收起了他的傲慢,在他的《论无穷级数及其有限和》中提出了这样的恳求:“如果谁能解决并告知这个我们无能为力的问题,我们将不胜感谢。”2
,挡住了他的去路。他可以采用我们现在所知的比较检验法证明这个级数收敛于某个小于2的数,但是他未能求出这个数。雅各布收起了他的傲慢,在他的《论无穷级数及其有限和》中提出了这样的恳求:“如果谁能解决并告知这个我们无能为力的问题,我们将不胜感谢。”2
2 Jakob Bernoulli, Ars conjectandi, p. 254。
正如我们在后面要看到的,对于伯努利提出的难题,整整一代人不得其解,直到最后由历史上最卓越的分析学家之一的欧拉给出问题的答案。
雅各布·伯努利堪称一位无穷级数的大师。他那位具有同样天赋的弟弟约翰有着自己感兴趣的研究领域。下面我们来讨论其中约翰称为“指数微积分”的问题。
约翰和x^x
在1697年的一篇论文中,约翰·伯努利从下述一般法则开始他的讨论:“一个对数函数无论多么复杂,它的微分等于函数表达式的微分除以表达式。” 1 例如,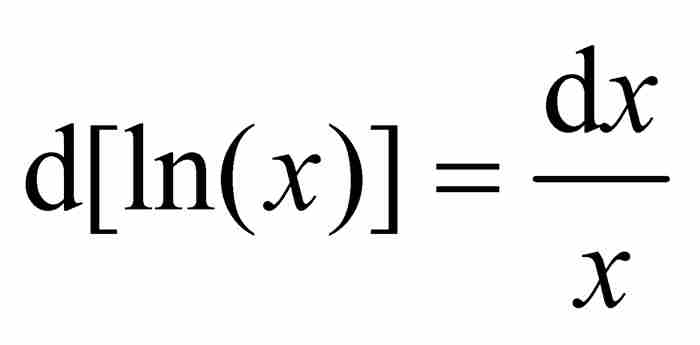 ,或者
,或者
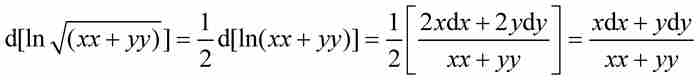
1 Johannis Bernoulli, Opera omnia, vol.1, Georg Olms, Hildesheim, 1968, p. 183。
在最后的这个表达式中,我们保留了伯努利的原有记号。在当时的数学出版物中,高次幂的写法与现在相同,但是通常把平方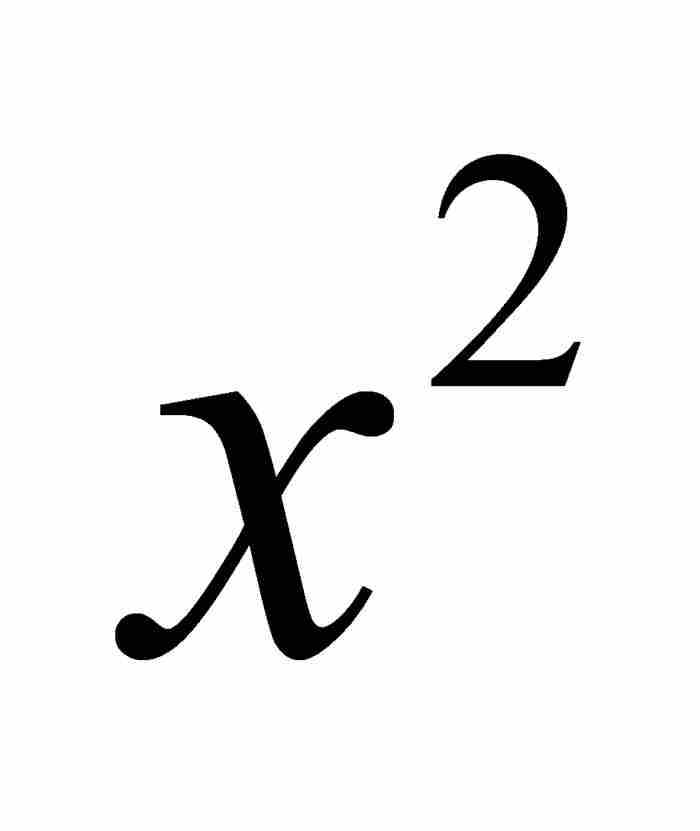 写成
写成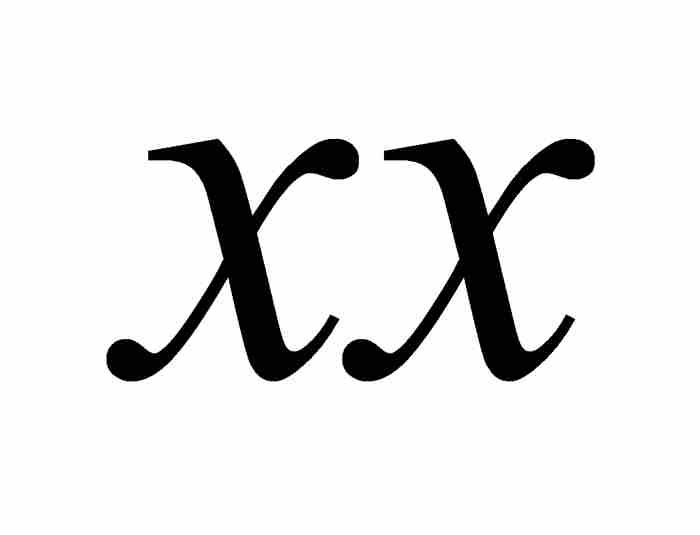 。此外,顺便说一下,伯努利还用lx表示
。此外,顺便说一下,伯努利还用lx表示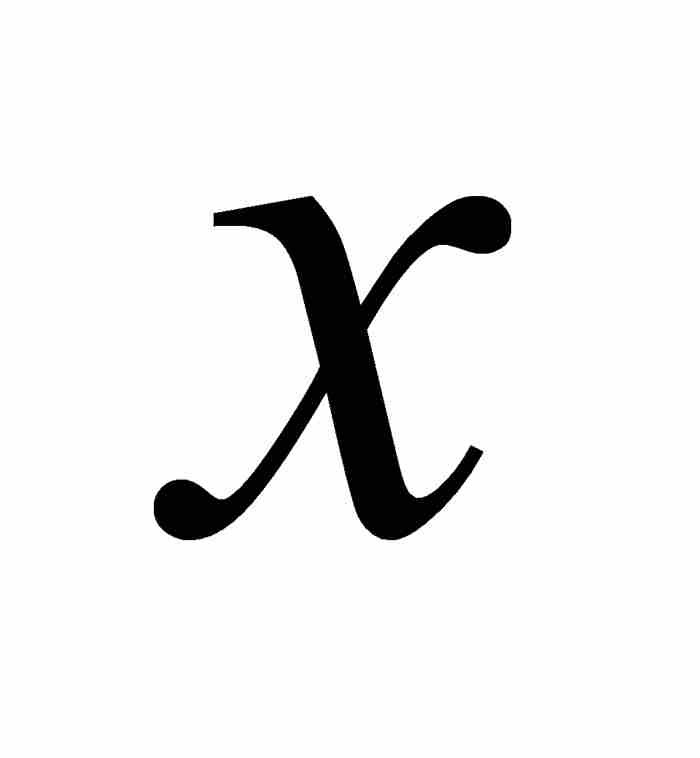 的自然对数。
的自然对数。
约翰给出了对应的积分公式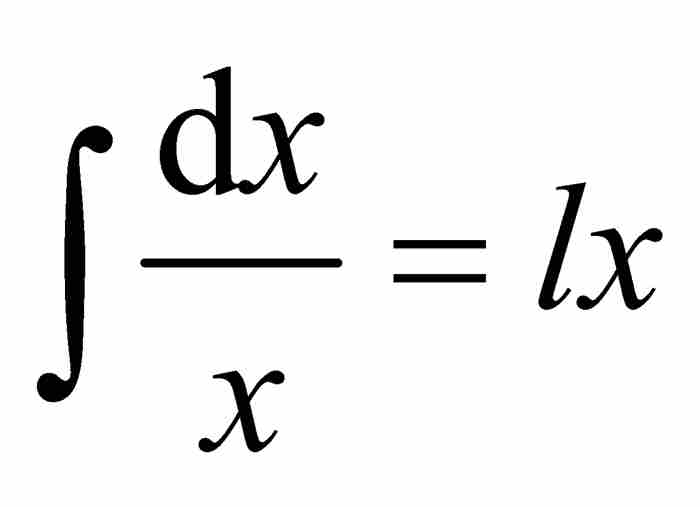 。在他学术生涯的早期,对于这一点的理解极为混乱,他相信
。在他学术生涯的早期,对于这一点的理解极为混乱,他相信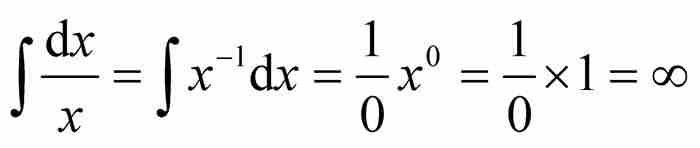 ,这是一种对指数法则的滥用,今天许多初学微积分的学生也有这样的错误理解。2 幸好约翰改正了他的错误。
,这是一种对指数法则的滥用,今天许多初学微积分的学生也有这样的错误理解。2 幸好约翰改正了他的错误。
2 Johannis Bernoulli, Opera omnia, vol.3, p. 388。
凭借这些预备知识,约翰作出承诺,他要用“由我首先创立的”法则去获取丰硕的知识成果,“用以前没有被发现的或者不是广为人知的知识去充实这座新的微积分的宝库”。3 也许他最感兴趣的例子莫过于图3-2所示的曲线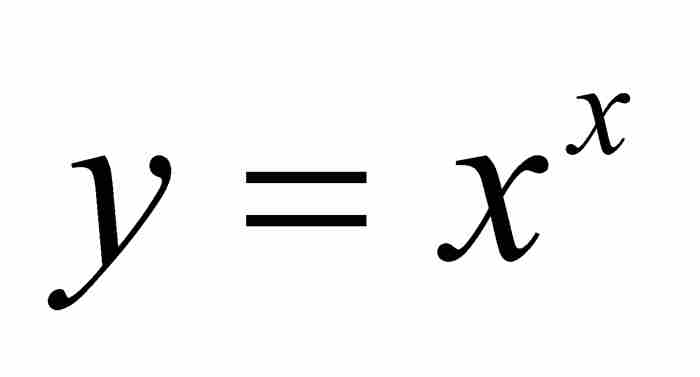 。
。
3 Johannis Bernoulli, Opera omnia, vol.3, p. 376。
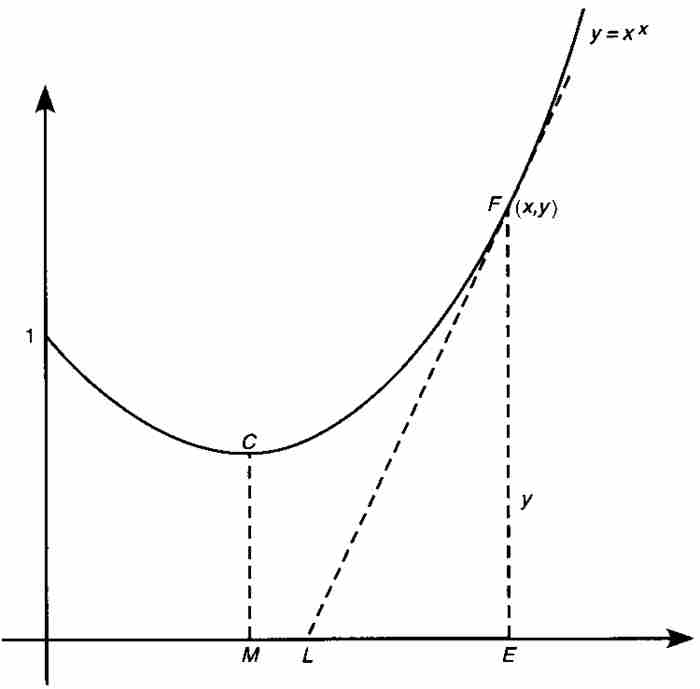
图 3-2
约翰从曲线上任意一点F求出次切距,即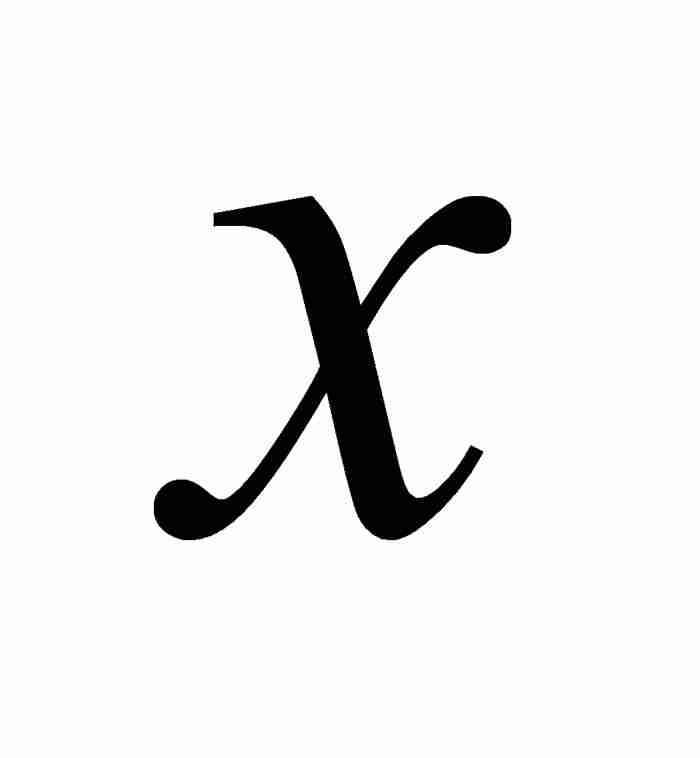 轴上切线下方的线段LE。为做到这一点,他首先对曲线方程两端取对数:
轴上切线下方的线段LE。为做到这一点,他首先对曲线方程两端取对数: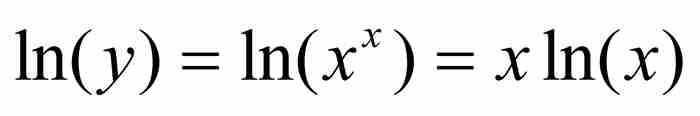 。然后他利用自己的法则求微分:
。然后他利用自己的法则求微分:
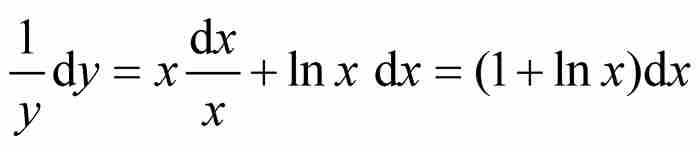
但是,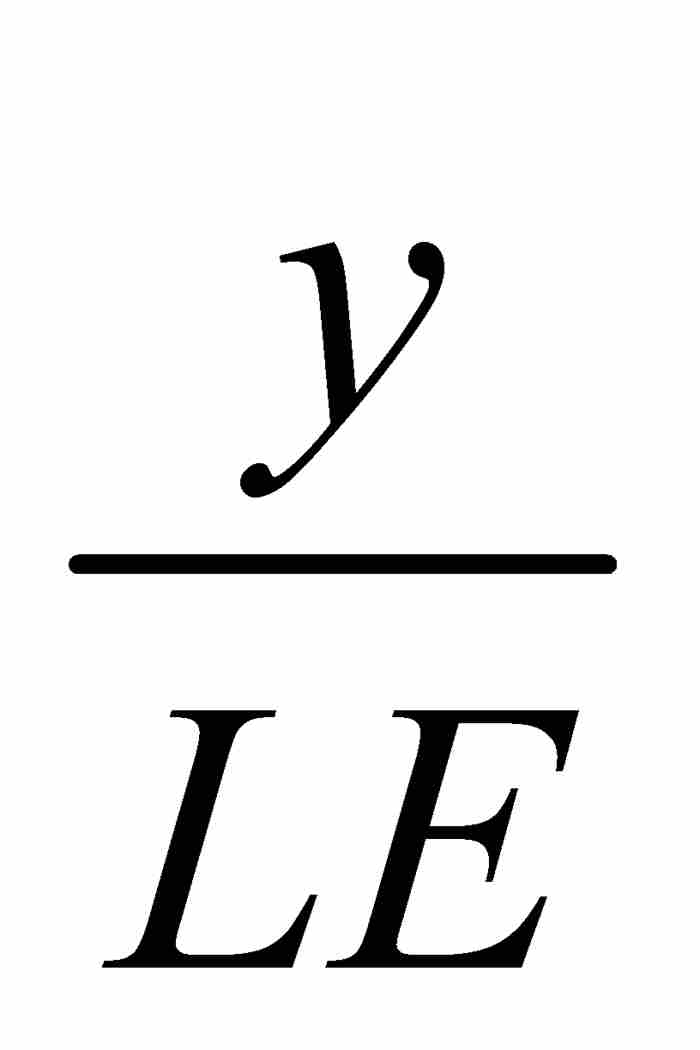 =切线的斜率=
=切线的斜率=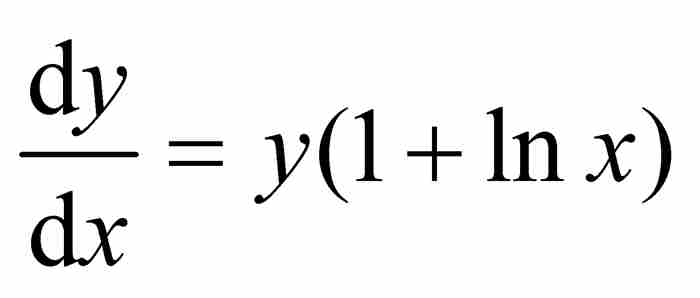 ,他由此求出次切距的长度
,他由此求出次切距的长度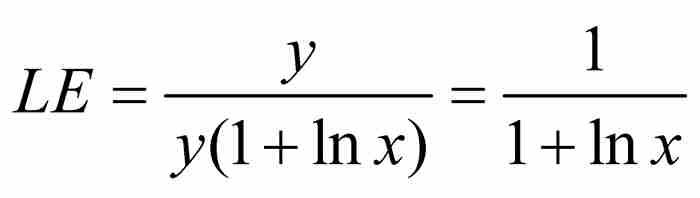 。
。
伯努利下一步就是寻找曲线的极小值,他将其称为“所有纵坐标的最小值”。当切线处于水平方向或者等价于次切距为无穷大时,得到曲线的极小值。为了确定当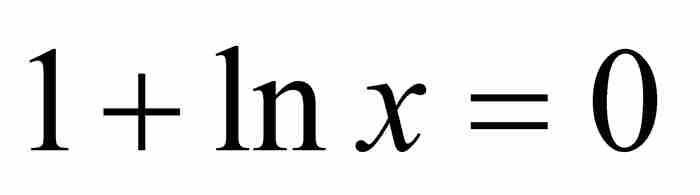 时x的值,约翰描述了一个颇为复杂的几何步骤。4
时x的值,约翰描述了一个颇为复杂的几何步骤。4
4 Johannis Bernoulli, Opera omnia, vol.1, pp. 184-185。
他的推理无懈可击,但是他的答案的形式按照当今的判别标准,看起来不是最佳的。由于指数函数的引进是几十年之后的事情,所以,约翰受到制约,他缺乏一种用于简单表达结果的记号。现在我们可以求出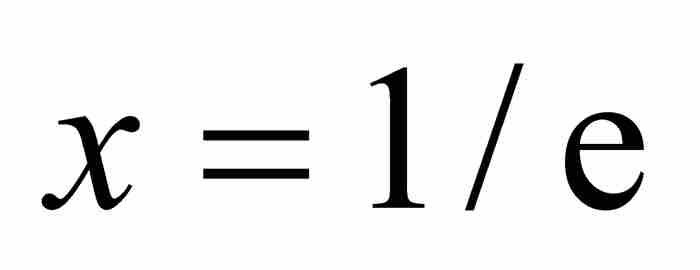 ,再确定xx的最小值,也就是图3-2中线段CM的长度,等于
,再确定xx的最小值,也就是图3-2中线段CM的长度,等于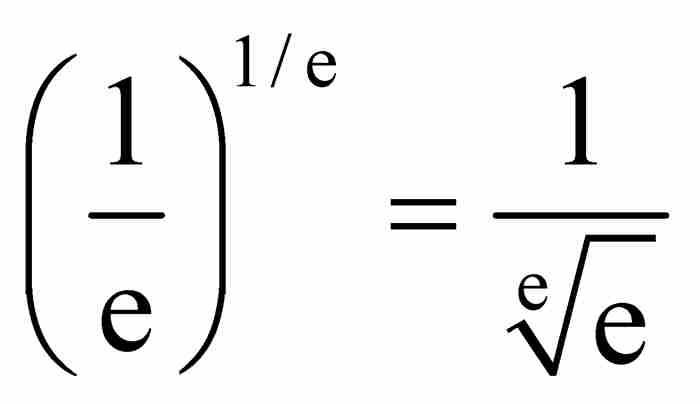 ,这个值近似为0.6922。不言而喻,这个答案决不是显而易见的。
,这个值近似为0.6922。不言而喻,这个答案决不是显而易见的。
至此,约翰只不过作好了继续前进的准备。他在1697年的另一篇论文中,解决了一个更为棘手的问题:求他的曲线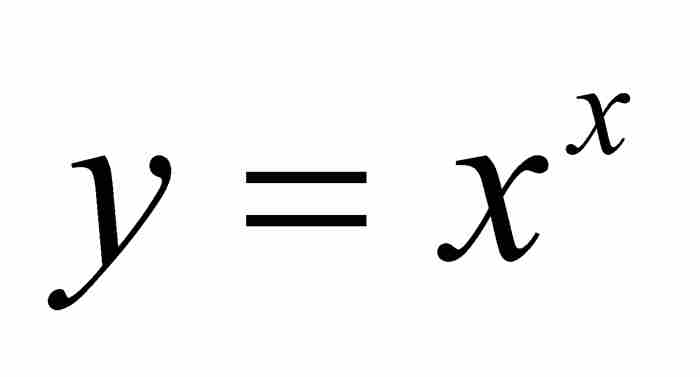 之下从
之下从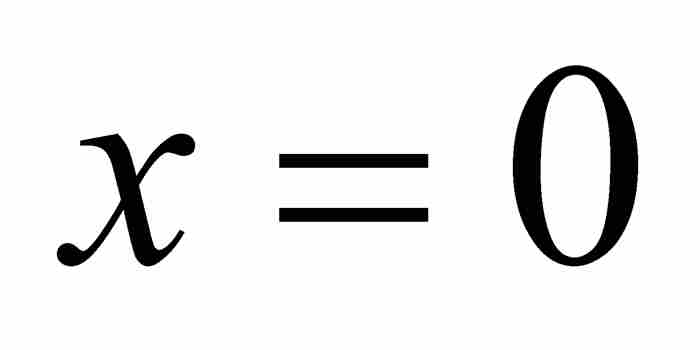 到
到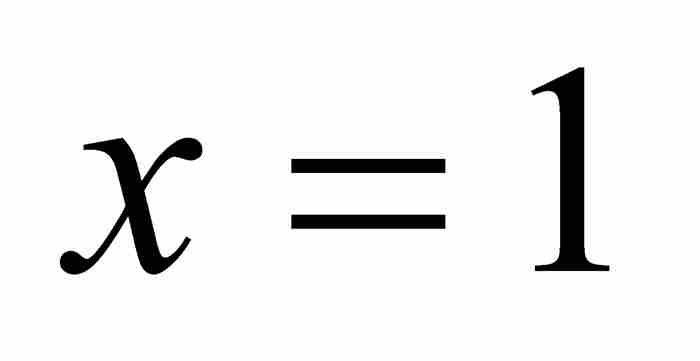 的区域的面积。就是说,他想求
的区域的面积。就是说,他想求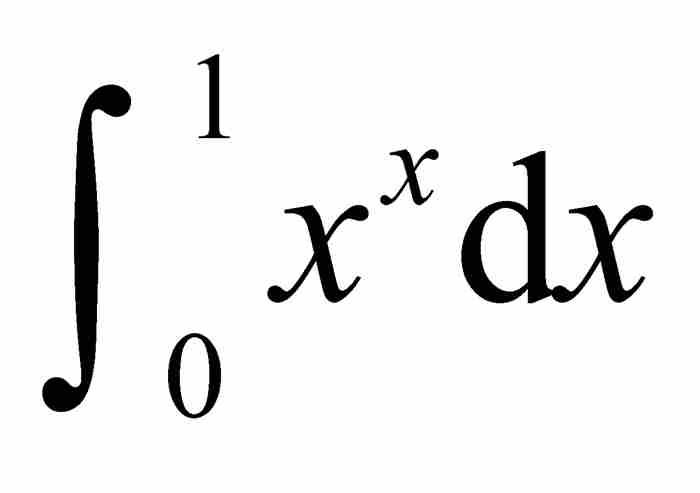 的值。相当令人吃惊,他求出了他一直试图寻找的答案。5
的值。相当令人吃惊,他求出了他一直试图寻找的答案。5
5 Johanis Bernoulli, Opera omnia, vol.3, pp. 376-381。
这个论证需要两个前提条件。他将第一个条件表述如下:
如果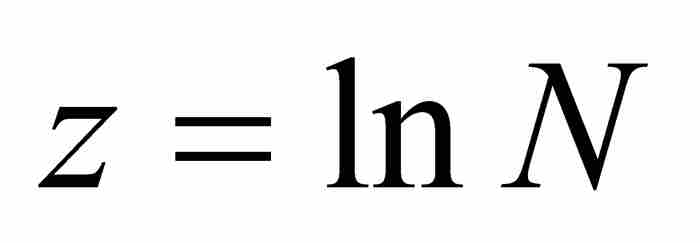 ,那么
,那么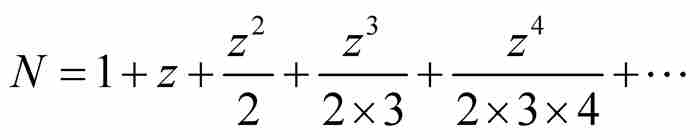
从这里,我们看出N的表达式是指数级数。如果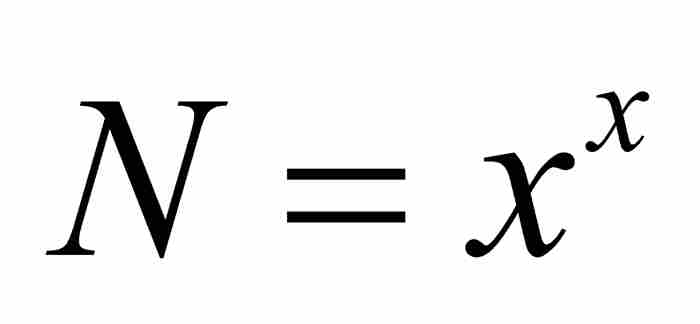 ,那么
,那么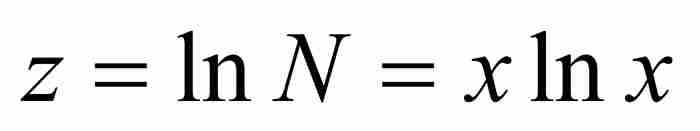 ,而约翰推导出
,而约翰推导出
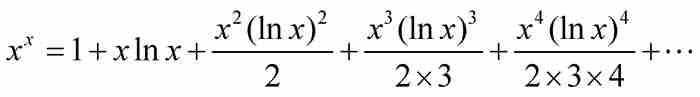 (3)
(3)
约翰的目标是通过对每一项积分求和来求这个和的积分。为此,他需要求积分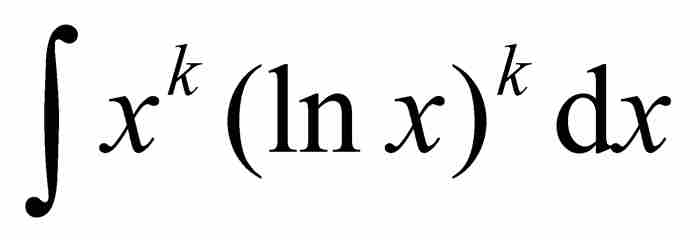 的公式。他采用递归的方法产生如下所示的积分表。
的公式。他采用递归的方法产生如下所示的积分表。
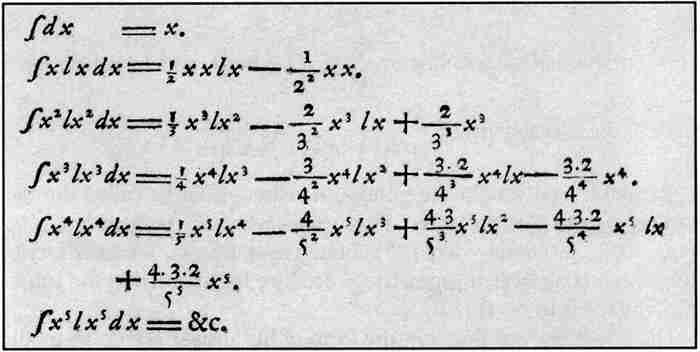
约翰·伯努利的积分表(1697)
一种现代的方法则是利用分部积分证明约化公式
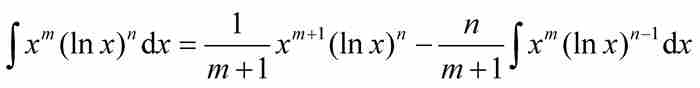 (4)
(4)
对于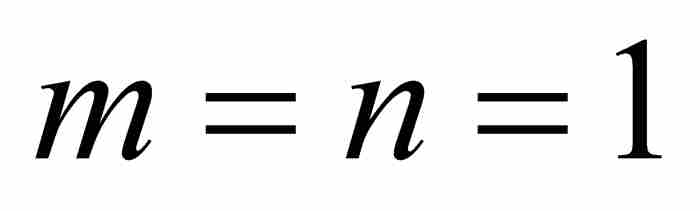 ,式(4)中的递归公式给出
,式(4)中的递归公式给出
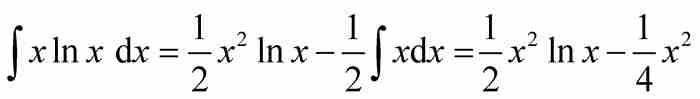
(像伯努利和他同时代的数学家一样,我们忽略了积分公式后面的任意常数项“+C”。)对于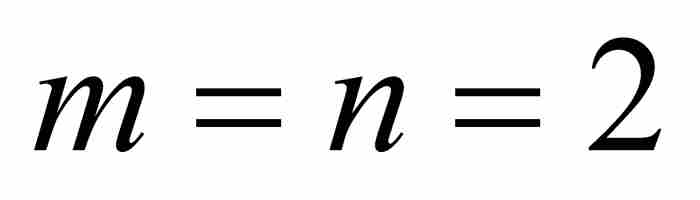 ,得到
,得到
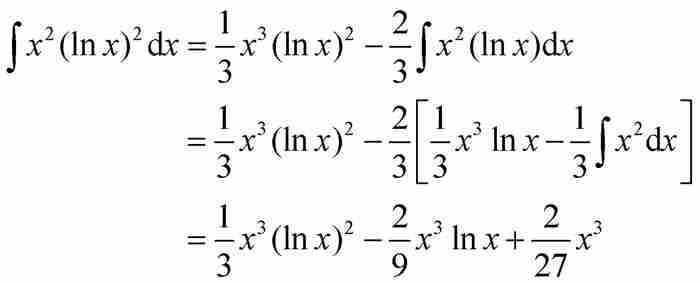
其中我们已经应用了取m=2和n=1时的公式(4)。
通过这种方式,我们重新得到了伯努利的积分表。同式(3)的指数级数一样,这也是求解他的奇特问题的关键。
定理 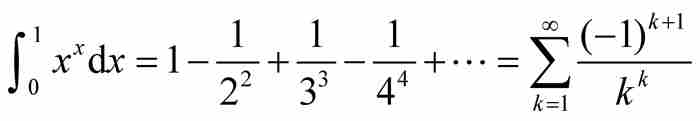 。
。
证明 由式(3),
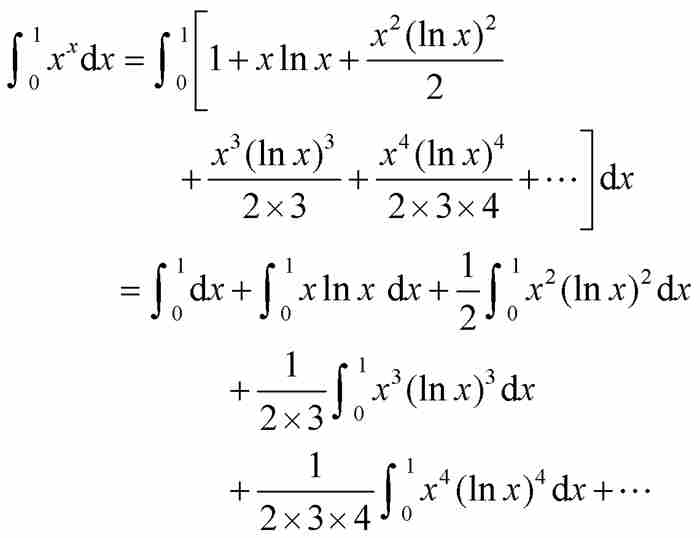
其中伯努利毫不犹豫地用积分的级数替换了级数的积分。他利用他的积分表中的公式继续推导:
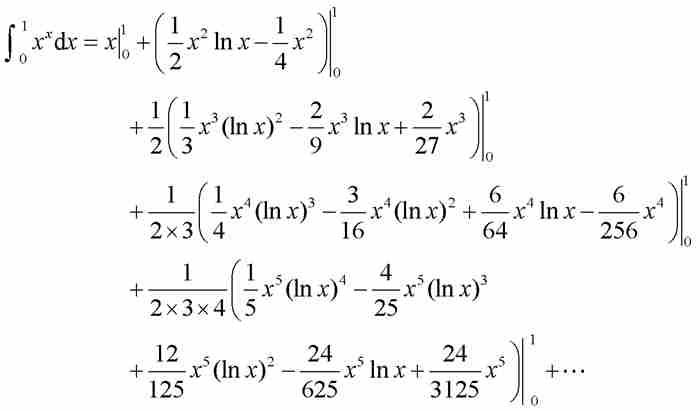
在这里,他注意到代入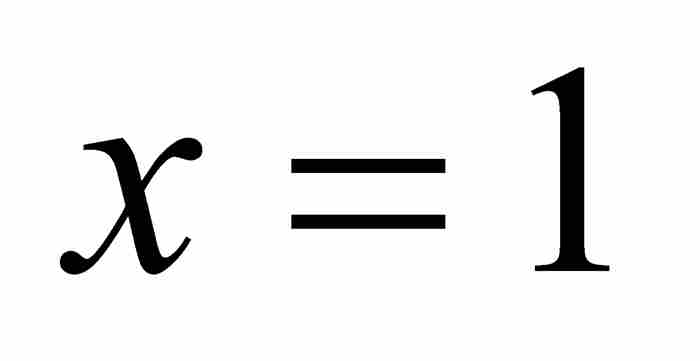 ,“所有含自然对数lx或lx任意乘方的项都化为零,因为1的对数等于零”。6 这是很精彩的,但是现代读者可能感到困惑,因为他没有提及代入x = 0会产生像
,“所有含自然对数lx或lx任意乘方的项都化为零,因为1的对数等于零”。6 这是很精彩的,但是现代读者可能感到困惑,因为他没有提及代入x = 0会产生像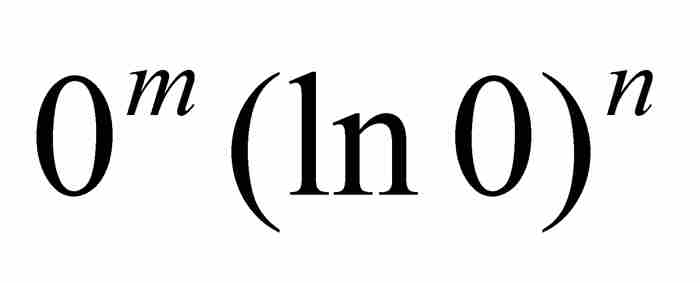 这样的不定式。今天,我们可以应用洛必达法则(最恰当的选择!)证明
这样的不定式。今天,我们可以应用洛必达法则(最恰当的选择!)证明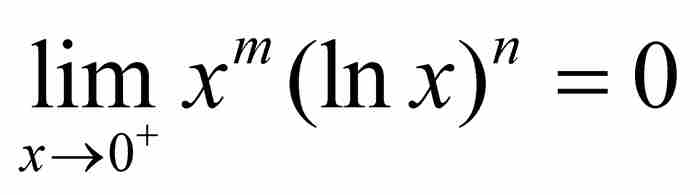 。
。
6 Johanis Bernoulli, Opera omnia, vol.3, p. 381。
在任何情况下,在如此多的项消失以后,伯努利保留下
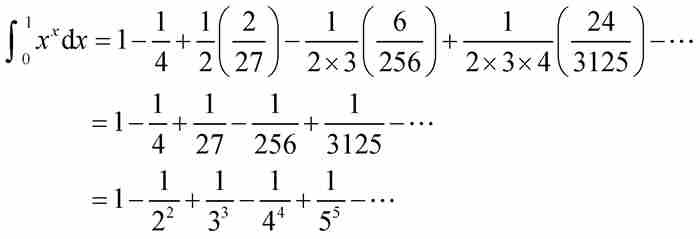
这个级数给出曲线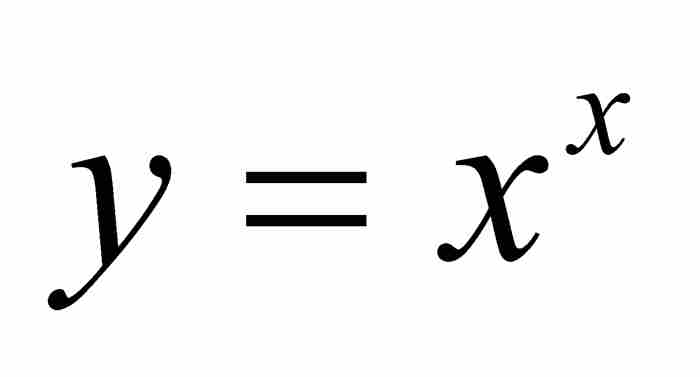 下单位间隔内的面积,这是十分引人注目的。除了级数极好的对称性和直观性以外,约翰还发现了它具备另外一种特性。他写道:“这个奇妙的级数收敛得非常快,第10项的值只占总和的10亿分之一。” 7 无疑,仅需要计算很少的几项就得到
下单位间隔内的面积,这是十分引人注目的。除了级数极好的对称性和直观性以外,约翰还发现了它具备另外一种特性。他写道:“这个奇妙的级数收敛得非常快,第10项的值只占总和的10亿分之一。” 7 无疑,仅需要计算很少的几项就得到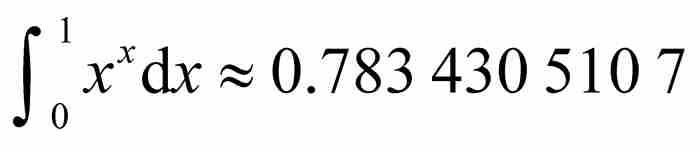 ,这是精确到第10位小数的数值。
,这是精确到第10位小数的数值。
7 Johanis Bernoulli, Opera omnia, vol.3, p. 377。
从本章的例子明显看出,雅各布·伯努利和约翰·伯努利确实是戈特弗里德·威廉·莱布尼茨的得意门生。用现在的话来说,莱布尼茨的微积分在他们的手中变成“用户友好的”。这兄弟二人使在他们之前原本很深奥的微积分成为非常容易理解的学科。
此外,约翰还留下了另外一份“遗产”。在18世纪20年代,他培养了一名前途无量的年轻的瑞士学生。这位学生的名字是莱昂哈德·欧拉,我们将在下一章介绍他的成就。