第2章 莱布尼茨
04-13Ctrl+D 收藏本站

戈特弗里德·威廉·莱布尼茨(1646—1716)
微积分的两位创建者都因为在其他的方面也有建树而更闻名,这也许是独一无二的。在公众的心目中,艾萨克·牛顿往往被看成一位物理学家,而微积分的共同创建者戈特弗里德·威廉·莱布尼茨则多半被认为是一位哲学家。这既令人不悦又让人欣喜,不悦是因为这表明人们无视他们在数学上的贡献,而欣喜是由于人们公认创建微积分需要超越一般天才的奇才。
莱布尼茨兴趣广泛,贡献突出,具有渊博的知识。除了哲学和数学,他在历史、法学、语言、神学、逻辑学和外交方面都有杰出的成就。在年仅27岁时,莱布尼茨就凭借他发明的一台机械计算器加入了英国皇家学会,这台可以进行加、减、乘、除运算的机器以其复杂性被公认为一次革命。1
1 Joseph E. Hofmann, Leibniz in Paris: 1672-1676, Cambridge University Press, 1974, pp. 23-25和p. 79。
虽然晚于牛顿,并且出生在另一个国度,莱布尼茨还是和牛顿一样有着一段热烈进行数学研究的时期。牛顿在17世纪60年代中期已经在剑桥大学建立了他的流数思想,而莱布尼茨是在十年之后在巴黎履行外交使命时完成他自己的奠基工作的。这使牛顿捷足先登,也让牛顿和他的同胞们后来认定这是事关优先权的唯一凭据。但是当莱布尼茨发表他的微积分成果时,牛顿的《分析学》和其他论文仍然以手稿的形式尘封着。关于接着发生的微积分发明权应该归功于哪一位的争论,已有很多著述,而且这并不是一个动听的故事。2上百年来,现代学者们终于抹去了国家和个人的感情因素,认定牛顿和莱布尼茨各自独立创建了微积分。像水到渠成的一种观念的产生一样,微积分到了“呼之欲出”的时刻,只是需要极端敏锐的和总揽其成的思想将它变成现实。牛顿恰恰具有这种思想。
2 例如,参考Rupert Hall, Philosphers at War, Cambridge University Press, 1980。
毫无疑问,莱布尼茨也具有这种思想。在1672年,他到巴黎担任外交官之前,莱布尼茨还是一个被认为对“阅读冗长的数学证明”缺乏耐心的新手。3他不满足于自己的知识,花费时间填补缺口,大量阅读令人敬仰的数学家们的著作,远至古代的欧几里得(公元前3世纪前后),近至他那个时代的帕斯卡(1623—1662)、巴罗以及他一度师从的克里斯琴·惠更斯(1629—1695)。开始的时候困难重重,但是莱布尼茨坚持了下来。他后来回忆说,尽管他还有很多不足,但是“不知从哪里来的自信让我坚信,只要努力我就可以成为他们中的一员”。4
3 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 11。
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p.12。
莱布尼茨取得的成功是激动人心的。他在一段回忆文章中写道,他很快就“作好进行独立研究的准备,因为我阅读数学文献就如同别人阅读浪漫的小说一样轻松”。5 在几乎是狼吞虎咽地吸收同时代的人的成果之后,莱布尼茨把他们远远地抛在后面,创造了微积分,从而使他在数学上赢得名垂青史的业绩。
5 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p.12。

莱布尼茨关于微分学的第一篇论文(1684)
与英吉利海峡对岸的牛顿不同,莱布尼茨愿意发表成果。微积分的第一个刊载形式是莱布尼茨1684年撰写的论文,这篇论文带有一个冗长的标题Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas, nec irrationales quantitates moratur; et singulare pro illis calculi genus,翻译过来是《一种求极大值与极小值以及求切线的新方法,它也适用于有理量与无理量以及这种新方法的奇妙类型的计算》。6 既然涉及求极大值与极小值以及求切线问题,毫无疑问,莱布尼茨的这篇文章是介绍微分法的。两年以后他又发表了另一篇介绍积分法的文章。即使处于早期阶段,莱布尼茨不但构造和整理了许多微积分的基本法则,而且已经用 表示 x 的微分和用
表示 x 的微分和用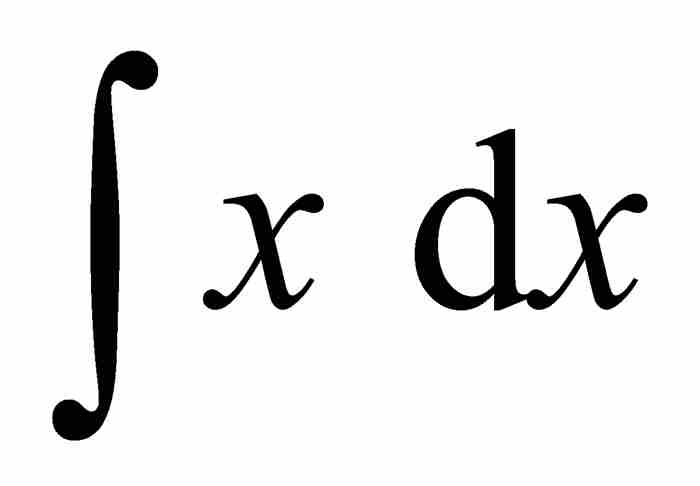 表示 x 的积分。他的卓越才能之一,正是后来拉普拉斯所说的提供了“一种非常恰当的符号”。7
表示 x 的积分。他的卓越才能之一,正是后来拉普拉斯所说的提供了“一种非常恰当的符号”。7
6 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, pp. 272-280。
7 Robert E. Moritz (ed.), Memorabilia Mathematica, MAA, 1914, p. 323。
在这一章,我们考察他在1673年至1674年间证明的两个定理。所讨论的大部分材料来自莱布尼茨的专著《微分学的历史和起源》,书中叙述了他创建微积分过程中发生的事情。8 我们讨论的第一个定理是很抽象的所谓变换定理。在它的推导中搀杂着几何技巧,虽然这一点现在不能引起人们的兴趣,而在当初却显示了他的数学天分,产生了我们现在所说的分部积分法的初期形式。第二个结果是第一个结果的推论,被称为“莱布尼茨级数”。如前面一章讨论的牛顿的成果一样,这种级数展开和基本积分方法的结合产生一个重要的和妙不可言的结果。
8 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, pp. 22-58。
变换定理
在17世纪中期,计算曲线之下的面积是一个热门话题,这也是莱布尼茨变换定理的主题。在图2-1中,假定我们要计算曲线AB下面的面积。莱布尼茨将这个区域的面积想象成是由无限多个无限小的矩形构成的。每个矩形的宽度为 ,长度为y,其中y随曲线AB的形状变化而改变。
,长度为y,其中y随曲线AB的形状变化而改变。
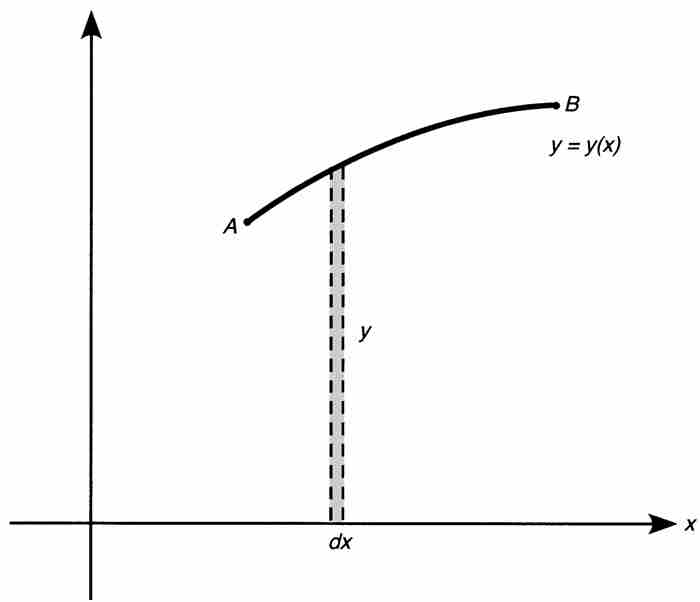
图 2-1
在我们看来,莱布尼茨的 的性质是不明确的。在17世纪,
的性质是不明确的。在17世纪, 被看作是最小的可能长度,一个无限小的不可能再分的长度。但是怎么可能有这样的事情呢?很明显,任意长度,即使是刀刃一样薄的长度,也可以分为两半。莱布尼茨关于这一点的解释无助于概念的澄清,他对问题的说明是难以理解的。下面是莱布尼茨在1684年之后的一份手稿中的一段文字:
被看作是最小的可能长度,一个无限小的不可能再分的长度。但是怎么可能有这样的事情呢?很明显,任意长度,即使是刀刃一样薄的长度,也可以分为两半。莱布尼茨关于这一点的解释无助于概念的澄清,他对问题的说明是难以理解的。下面是莱布尼茨在1684年之后的一份手稿中的一段文字:
关于……无限小,我们理解为……某种无限的小,所以每次分割本身都成为一个级别,只不过不是一个最后的级别。如果有谁希望将这些[无限小]理解为最终的事物……,那么,这也是可以的,而且也不会陷入关于延伸范围或者一般而论的无限连续统或者无限小的真实性的争论中,即使他认为这样的事是完全不可能的。1
1 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 150。
读者不必寻找这种概念的澄清,更无需自己去澄清。莱布尼茨看来选择了逻辑上的权宜之计,他作出补充,即使这些不可分量的性质尚不确定,它们依然可以作为“用于计算的有力工具”。我们再次看到了令后来的分析学家们进退维谷的数学泥潭。但是在1673年,莱布尼茨急切地向前推进,将这个逻辑上的问题留给下一代人解决。
回到图2-1,我们看到无限小矩形的面积为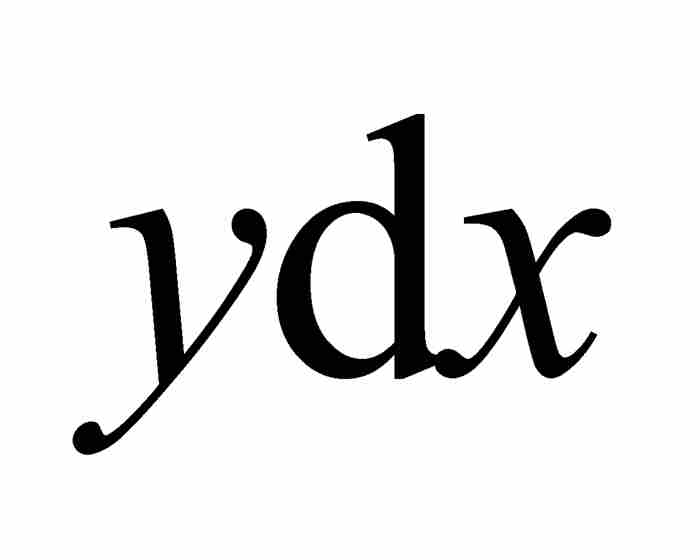 。为计算曲线AB下面的面积,莱布尼茨对这无穷多个面积求和。他选用伸长的“S”——代表“summa”(求和)——作为表示这个过程的记号。因此,这个面积表示成
。为计算曲线AB下面的面积,莱布尼茨对这无穷多个面积求和。他选用伸长的“S”——代表“summa”(求和)——作为表示这个过程的记号。因此,这个面积表示成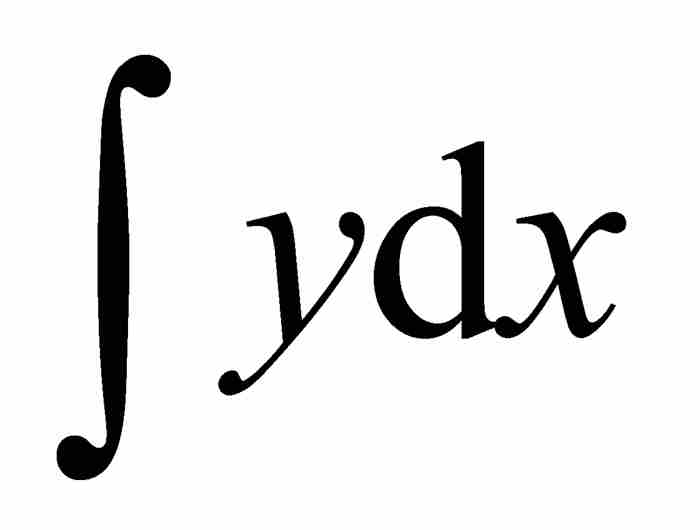 。从此以后,他的积分符号成了微积分的“标志”,向所有见到它的人宣告高等数学来临了。
。从此以后,他的积分符号成了微积分的“标志”,向所有见到它的人宣告高等数学来临了。
提出一个表示面积的记号是一回事,而掌握怎么计算面积完全是另一回事。莱布尼茨的变换定理就是以解决这个计算问题作为目标。
图2-2说明了他的思想,其中再次显示曲线AB,求它下面的面积是我们的目标。P是曲线上任意一点,其坐标为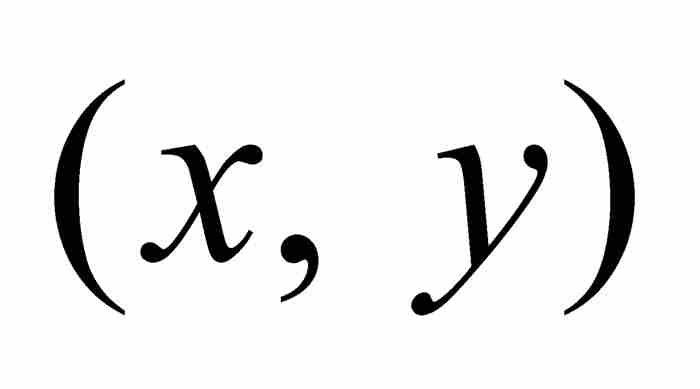 。莱布尼茨在P点画出切线 t,与纵坐标轴相交于点T(0, z)。莱布尼茨解释这个构造时说明“求一条切线意味着画一条直线连接曲线上距离无限小的两个点”。2 令
。莱布尼茨在P点画出切线 t,与纵坐标轴相交于点T(0, z)。莱布尼茨解释这个构造时说明“求一条切线意味着画一条直线连接曲线上距离无限小的两个点”。2 令 为x的无限小的增量,他建立一个无限小的直角三角形,以切线上的线段PQ为斜边,边长分别为
为x的无限小的增量,他建立一个无限小的直角三角形,以切线上的线段PQ为斜边,边长分别为 ,
, ,
, 的三角形放大后的图形显现在图2-3中。令α为切线的倾角。
的三角形放大后的图形显现在图2-3中。令α为切线的倾角。
2 Dirk Struik (ed.), A Source Book in Mathematics, 1200-1800, Harvard University Press, 1969, p. 276。
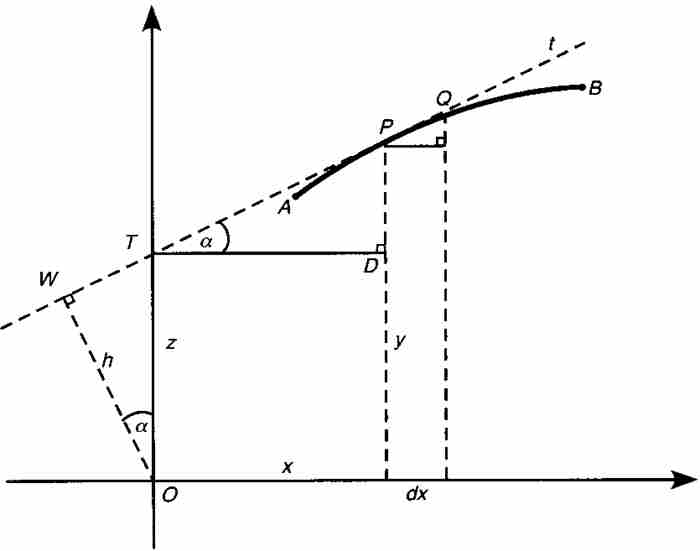
图 2-2
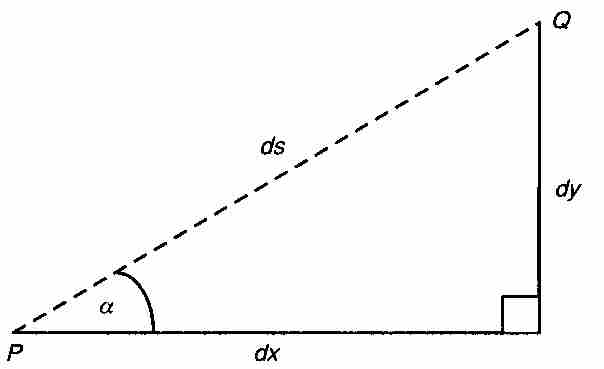
图 2-3
莱布尼茨强调,“虽然这个三角形是不确定的(无限小),但是……总可能找到一个相似于它的确定的三角形”。3 当然,有人会疑惑一个无限小三角形怎么可能同任何东西相似,但是这不是纠缠于细枝末节的时候。莱布尼茨把图2-2中的 看成与图2-3中的无限小三角形相似。于是有
看成与图2-3中的无限小三角形相似。于是有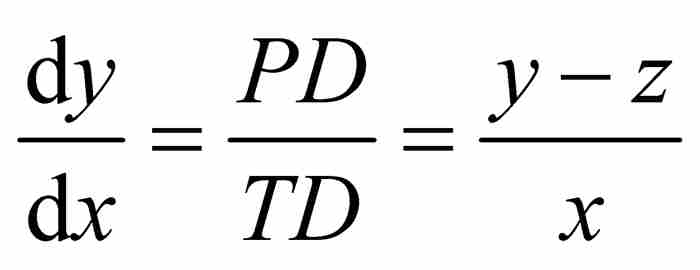 ,求解得到
,求解得到
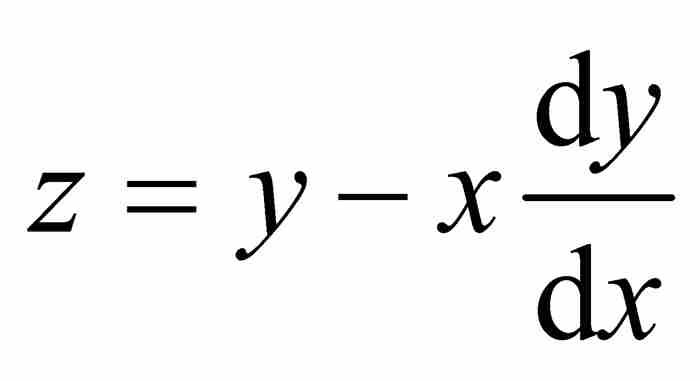 (1)
(1)
3 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 39。
下一步,莱布尼茨向左延长切线PT,并且从原点引出同这条延长线垂直的长度为 h 的线段OW(见图2-2)。由于 的值是α,可知
的值是α,可知 的值为
的值为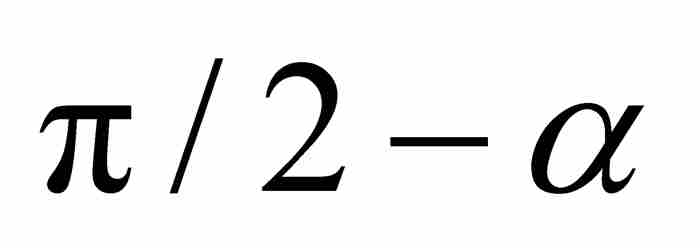 ,所以
,所以 的值也是α。这使得
的值也是α。这使得 相似于无限小的那个三角形,于是得到另一个比例关系
相似于无限小的那个三角形,于是得到另一个比例关系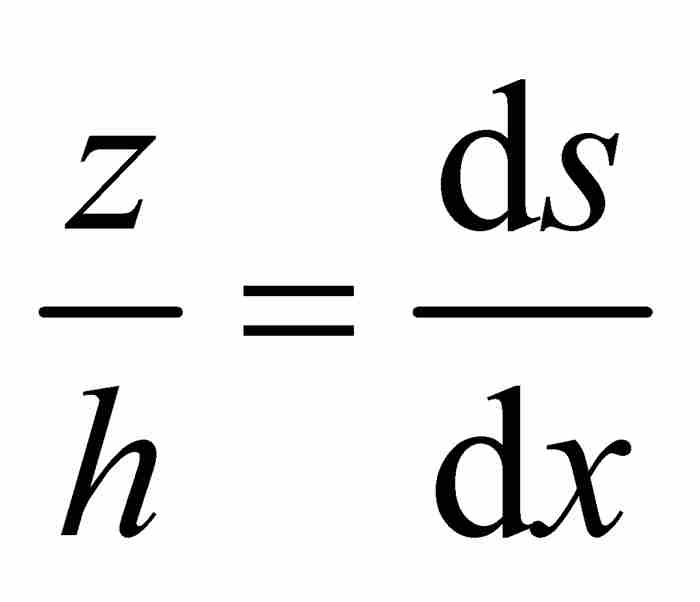 ,我们由此推出
,我们由此推出
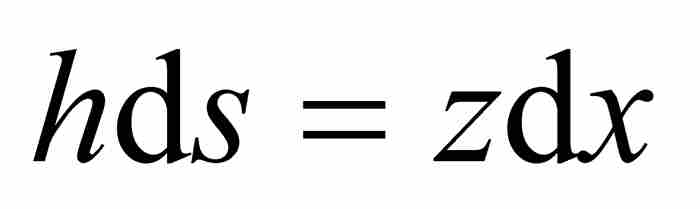 (2)
(2)
莱布尼茨然后画出从原点辐射出的 ,以无限小三角形的斜边PQ为底边。为避免使图2-2变得更为杂乱,我们将这个特别的三角形重新画在图2-4中。
,以无限小三角形的斜边PQ为底边。为避免使图2-2变得更为杂乱,我们将这个特别的三角形重新画在图2-4中。
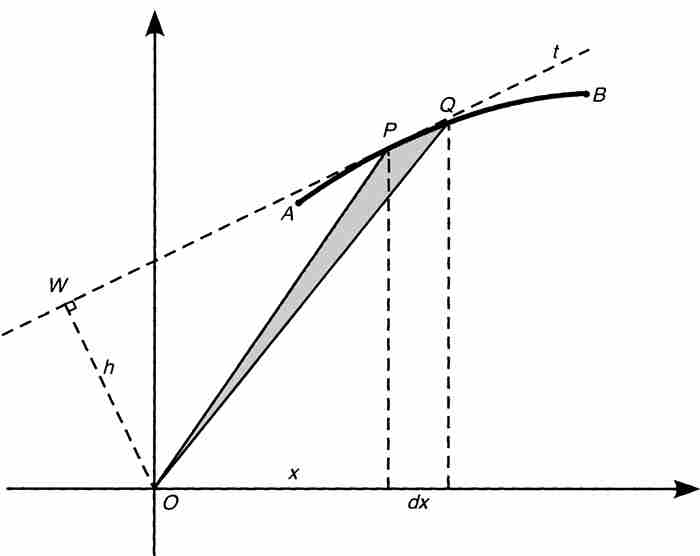
图 2-4
到这一步读者也许会想,莱布尼茨已经随波逐流地迷失在毫无目标的三角形的汪洋大海之中。然而,事实上,这个无限小斜三角形OPQ却成为他的变换定理的核心。由于三角形的底边为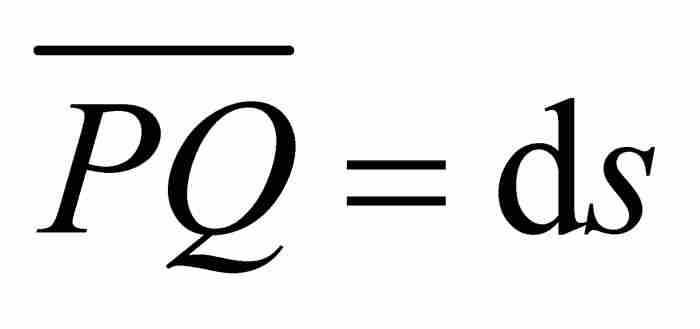 ,高为
,高为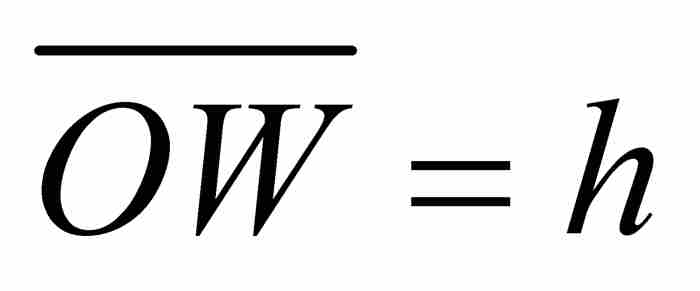 ,由此看出它的面积为
,由此看出它的面积为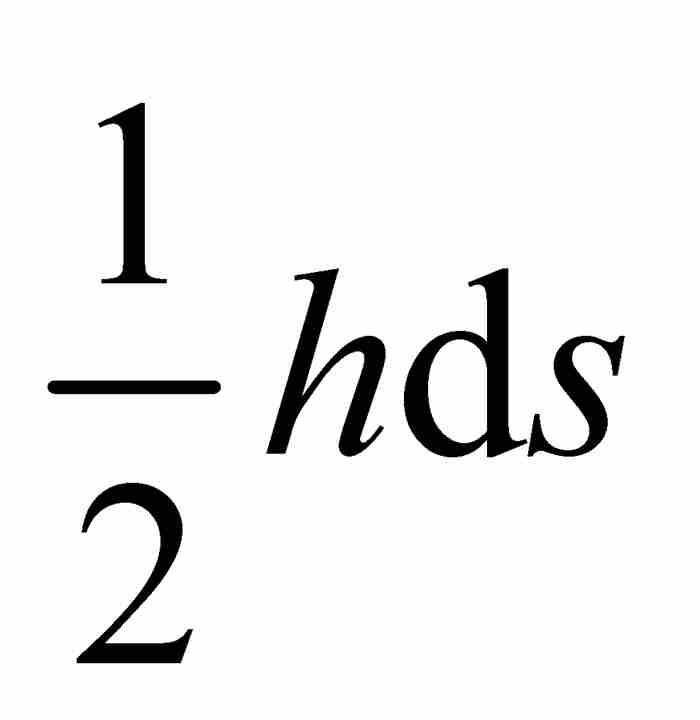 ,由上面的式(2)可知,这个面积恰好是
,由上面的式(2)可知,这个面积恰好是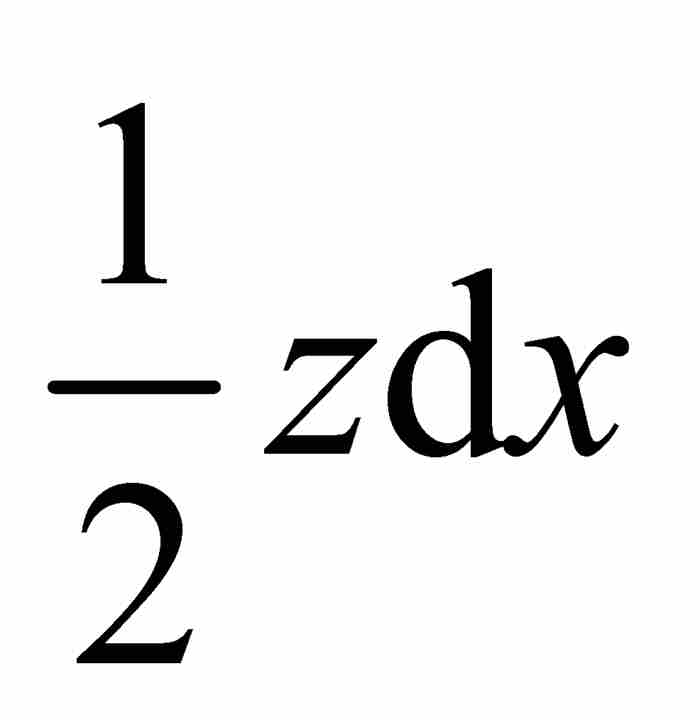 。
。
莱布尼茨画了无数个这样的无限小三角形,如图2-5所示,所有的三角形都是从原点辐射出来并终止于曲线AB。几年以后,莱布尼茨回忆起,他“偶然有机会用若干条通过同一点的直线将面积分成多个三角形,并且……察觉可以很容易从中获得某些结果”。4
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 42。
这种极透视三角形是非常关键的,因为莱布尼茨认识到图2-5中的楔形的面积就是那些无穷小三角形的面积之和,它们的面积的解析表达式已经在上面确定。就是说
面积(楔形)=三角形面积之和=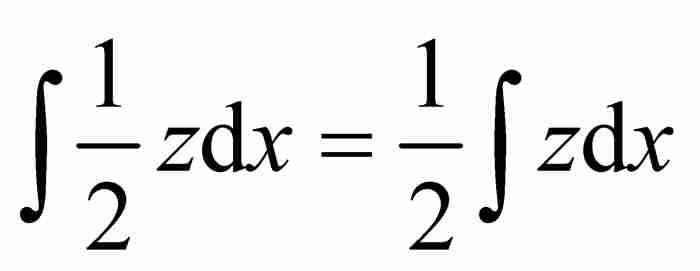 (3)
(3)
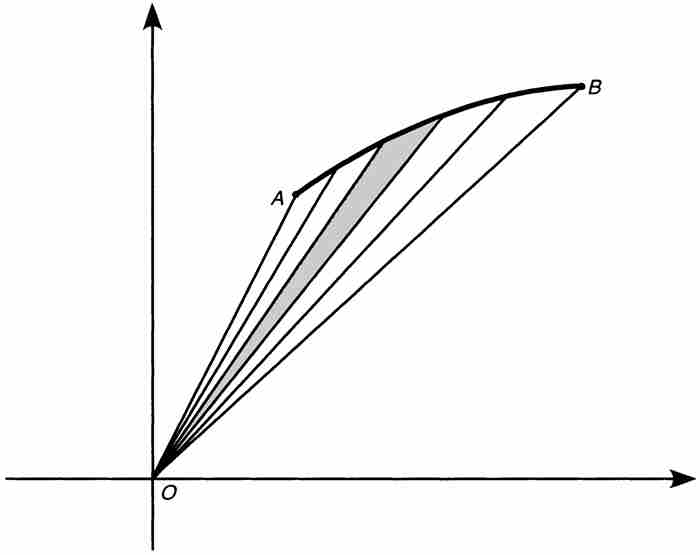
图 2-5
事实上,莱布尼茨的初衷并不是求这个楔形的面积。相反,他要寻求的是图2-1中曲线AB之下的面积,即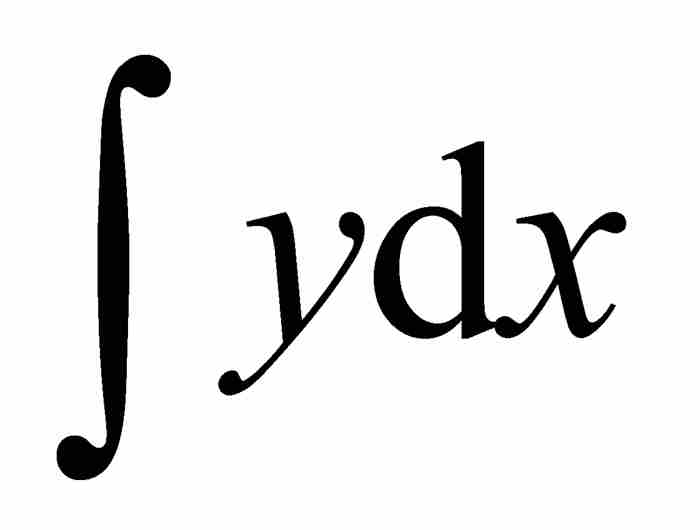 。幸好,只需要简单地修修补补就可以将讨论中的两个面积联系起来。图2-6中的几何图形表明:
。幸好,只需要简单地修修补补就可以将讨论中的两个面积联系起来。图2-6中的几何图形表明:
曲线AB下的面积=面积(楔形)+面积(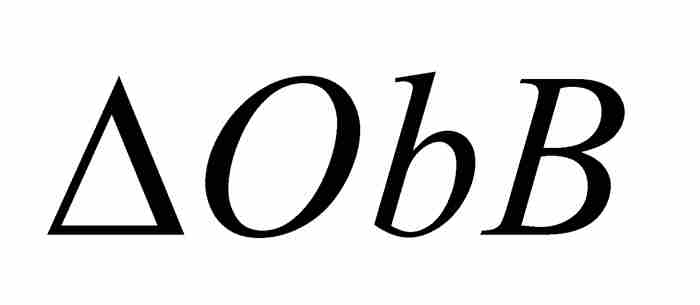 )-面积(
)-面积( )
)
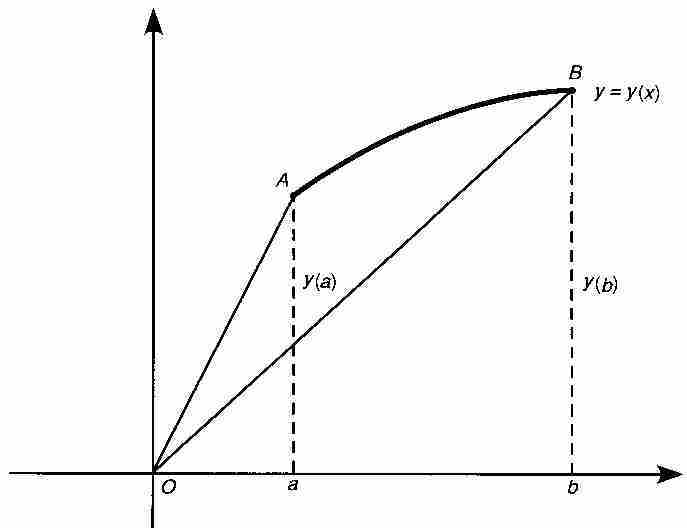
图 2-6
根据式(3),这个关系式从符号上等价于
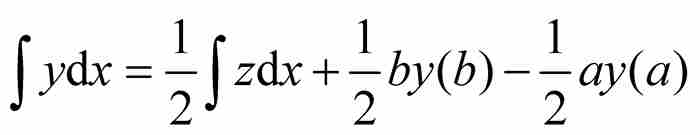 (4)
(4)
这就是最终的变换定理。定理的名称表示原来的积分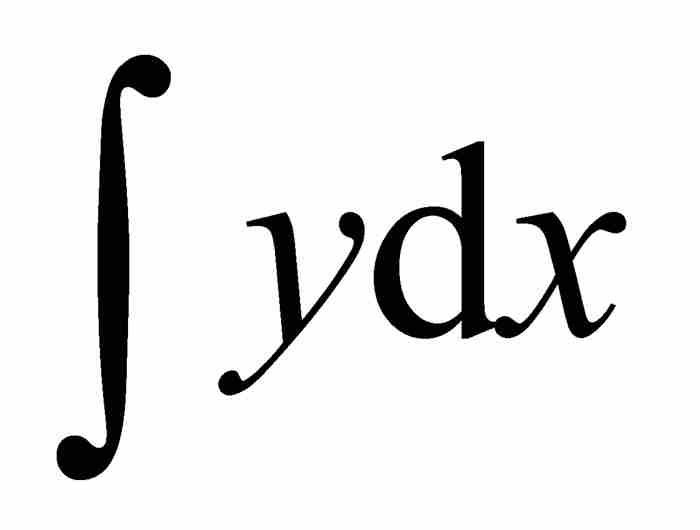 已经变换(或“转换”)成新积分
已经变换(或“转换”)成新积分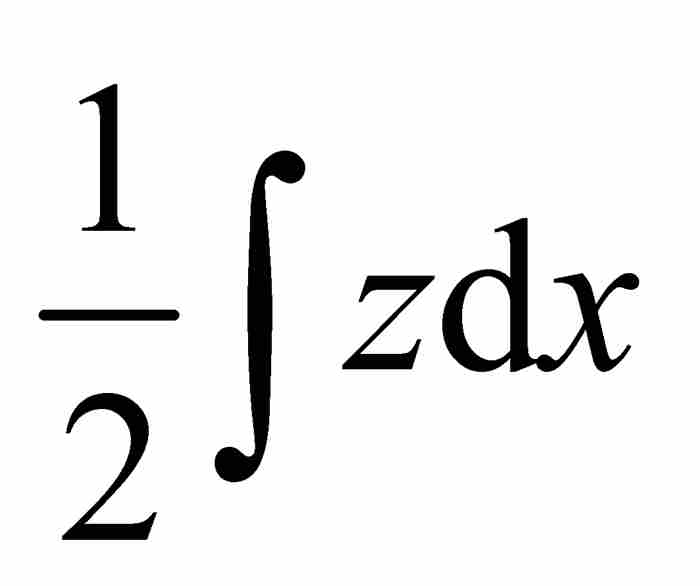 与常数
与常数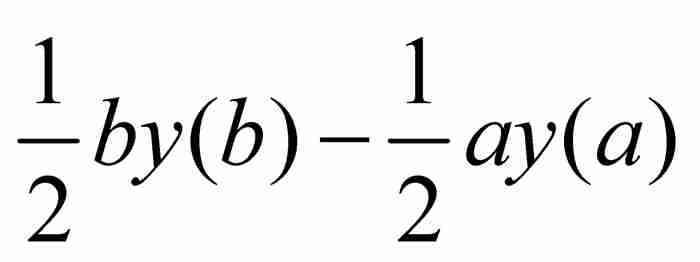 之和。如今,我们添加积分限(一个莱布尼茨没有用过的符号表示法)使得公式更称心如意,并且重写成
之和。如今,我们添加积分限(一个莱布尼茨没有用过的符号表示法)使得公式更称心如意,并且重写成
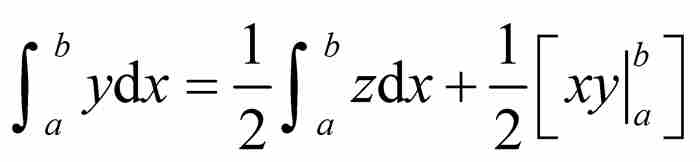 (5)
(5)
公式(5)由于至少以下两个原因而值得注意。
首先,“新的”对 z 的积分很可能比原来对 y 的积分更容易求值。如果是这样,z 就在求原来的面积中扮演了一个辅助的角色。对17世纪的数学家来说,一种称为割圆曲线的曲线就扮演这样的角色,也就是说,割圆曲线是一个求面积的助推器。如果从公式(5)能够产生一个更简单的积分,那么,这整个冗长的推导过程将获得补偿。正如我们立刻就会看到的,这种情况恰好出现在莱布尼茨级数的推导过程中。
其次,公式(5)中的关系具有理论意义。回想一下,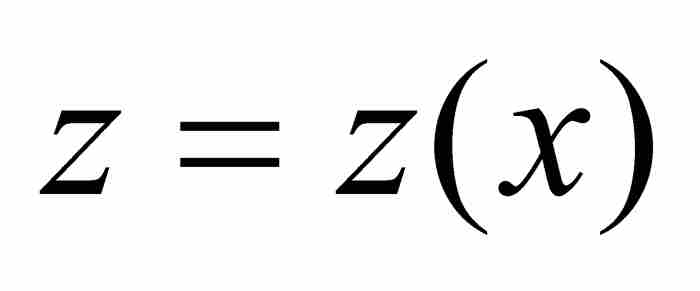 是曲线AB在点(x, y)处的切线在y轴的截距。因此 z 的值与切线的斜率有关,所以在这个复合的积分中注入了导数。这不禁使人意识到其中隐藏着重要的联系。
是曲线AB在点(x, y)处的切线在y轴的截距。因此 z 的值与切线的斜率有关,所以在这个复合的积分中注入了导数。这不禁使人意识到其中隐藏着重要的联系。
为更清楚地看到这一点,回想式(1)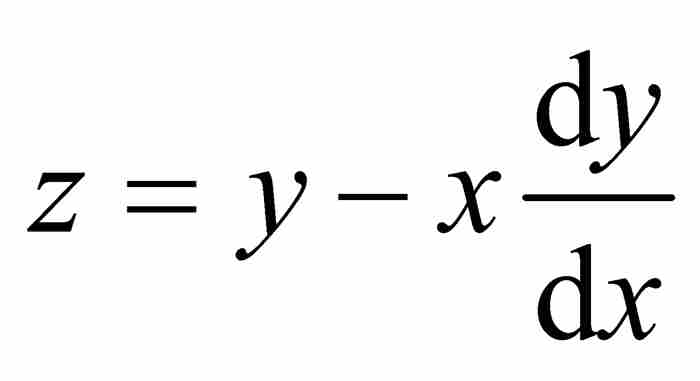 ,可得
,可得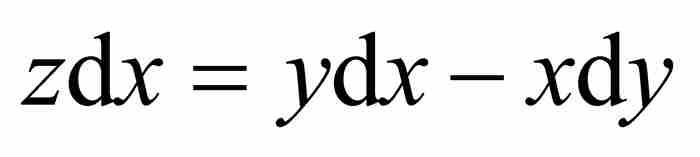 。代入式(4)得到
。代入式(4)得到
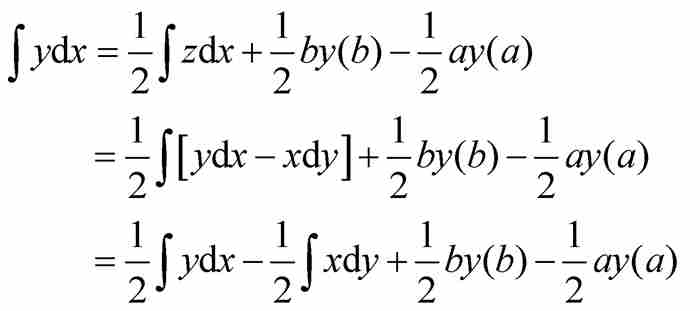
求解得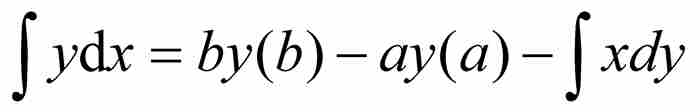 。
。
再加入积分限,给出
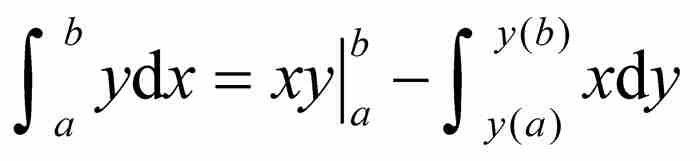 (6)
(6)
在图2-7中,式(6)在几何上的正确性是显而易见的,因为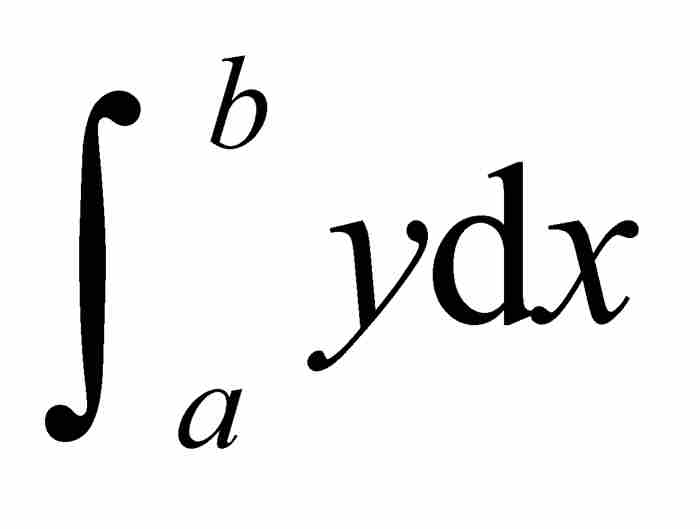 是所有纵向条形区域的面积,而
是所有纵向条形区域的面积,而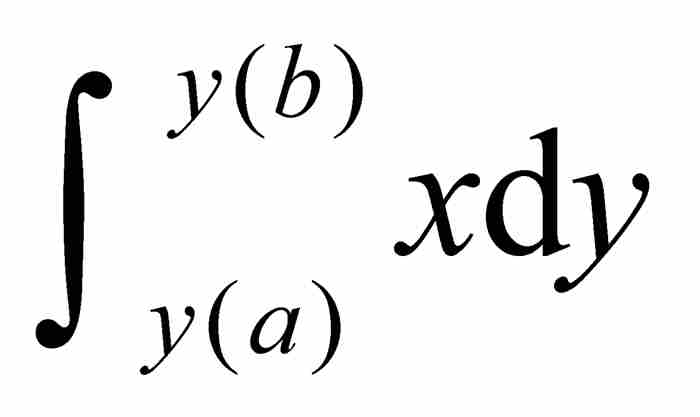 是所有横向条形区域的面积。这两部分面积的和显然是外围矩形和左下方小矩形面积之差。就是说,
是所有横向条形区域的面积。这两部分面积的和显然是外围矩形和左下方小矩形面积之差。就是说,
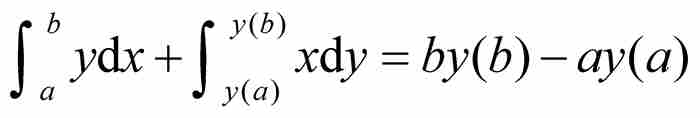
整理后即得式(6)。
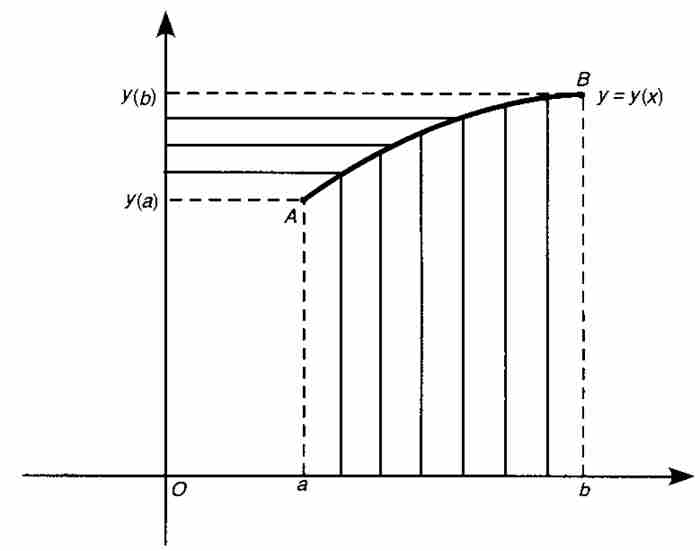
图 2-7
关于式(6)还要作一点说明:它看起来是大家熟悉的。这是理所当然的,因为它很容易地从著名的分部积分法公式
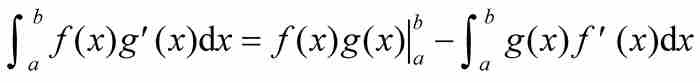
推出,只要在其中指定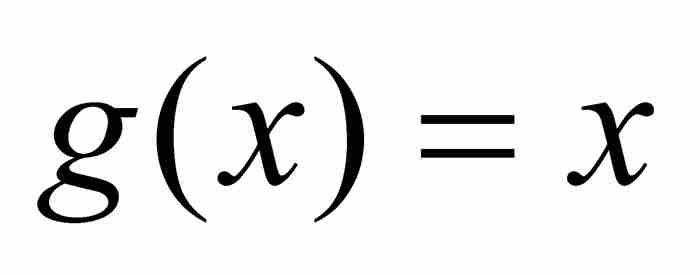 和
和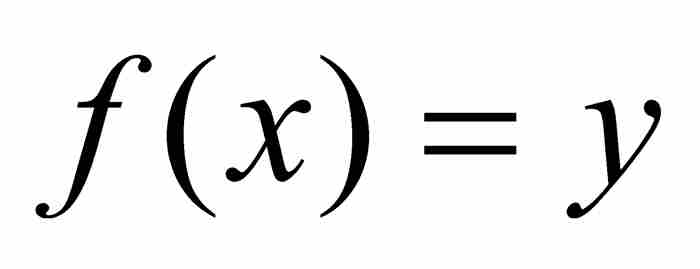 。在这种条件下
。在这种条件下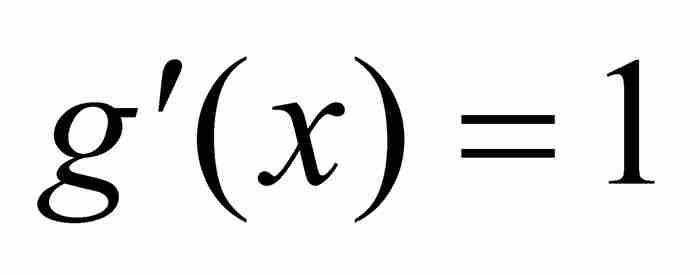 ,
,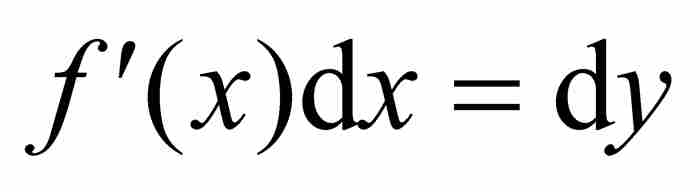 ,代入后就把分部积分公式转变成变换定理。莱布尼茨在使用无限小三角形、切线、相似三角形和楔形面积进行复杂推理以后,总之,在经过极其曲折的数学探索之旅以后,获得一个分部积分的实例,一位微积分的超级明星捷足先登,出人意料地走上舞台。
,代入后就把分部积分公式转变成变换定理。莱布尼茨在使用无限小三角形、切线、相似三角形和楔形面积进行复杂推理以后,总之,在经过极其曲折的数学探索之旅以后,获得一个分部积分的实例,一位微积分的超级明星捷足先登,出人意料地走上舞台。
这是令人兴奋的,但是莱布尼茨并没有停下脚步。在把他的变换定理应用于一条著名的曲线后,莱布尼茨发现了一个一直以他的名字命名的无穷级数。
莱布尼茨级数
莱布尼茨从一段圆弧开始。他特别考察半径为1和中心在点(1, 0)的圆,如图2-8所示。他把这个圆的四分之一作为他的一般变换定理里的曲线AB。下面马上就会看到,这是一个富有灵感的选择。
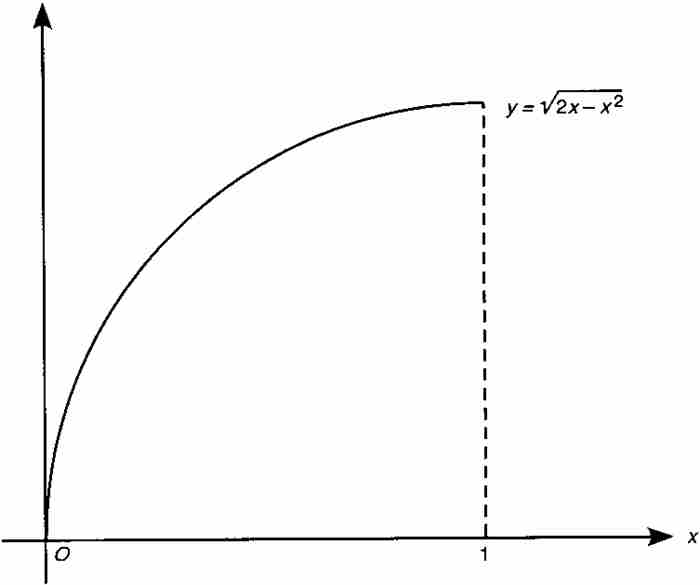
图 2-8
圆的方程为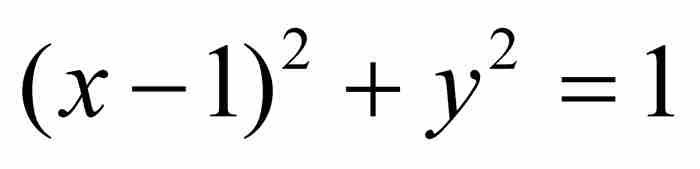 ,或者取另一种形式
,或者取另一种形式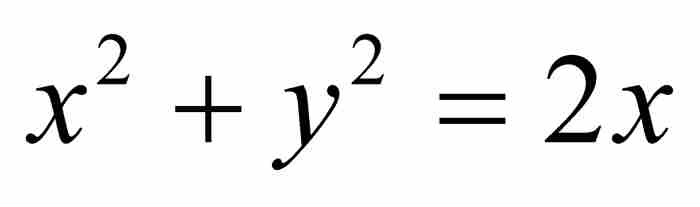 。由几何图形可知这段四分之一圆弧下的面积是
。由几何图形可知这段四分之一圆弧下的面积是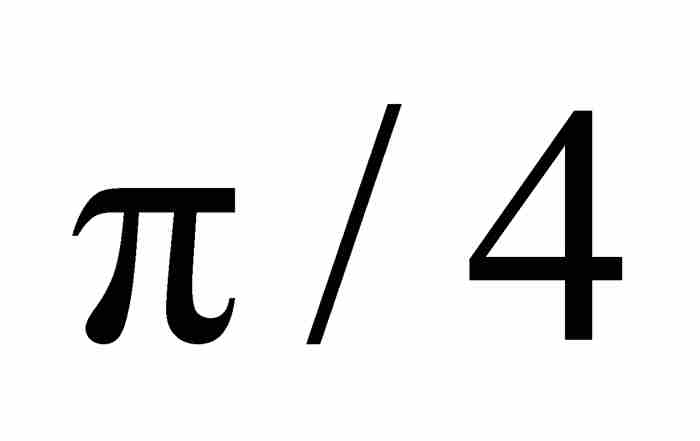 ,所以由式(1)和式(5)可得
,所以由式(1)和式(5)可得
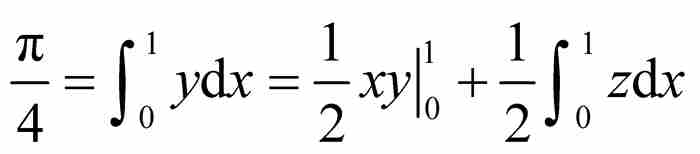 ,其中
,其中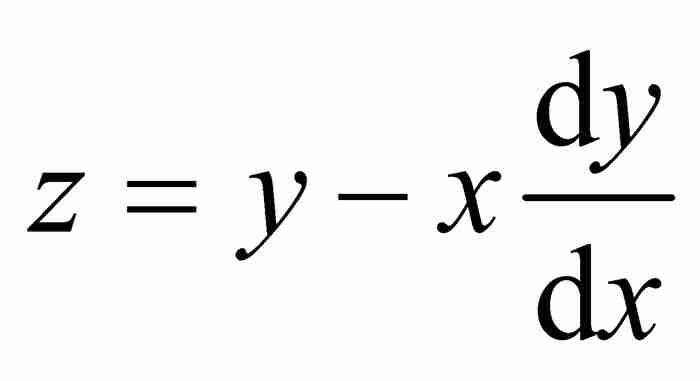
菜布尼茨利用他新创建的积分,对圆的方程求微分,得到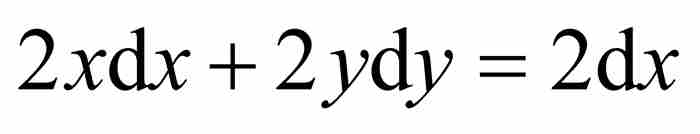 ,于是
,于是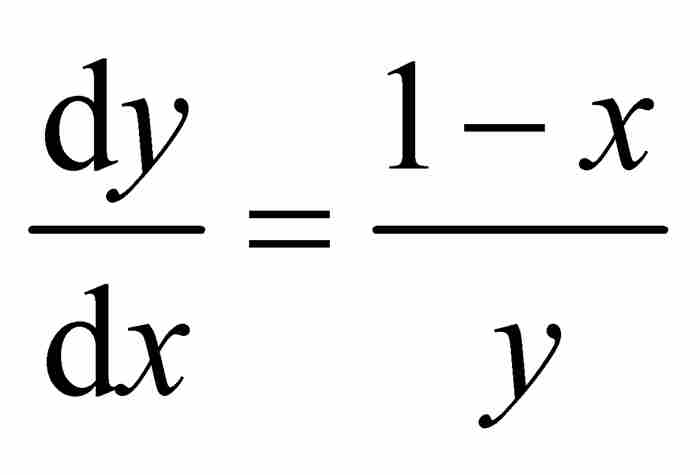 。这使式(1)简化成
。这使式(1)简化成
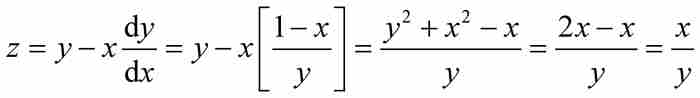
莱布尼茨的目标是求得由割圆曲线z的项来表示x的表达式,因此他将上式平方并利用圆的方程,得到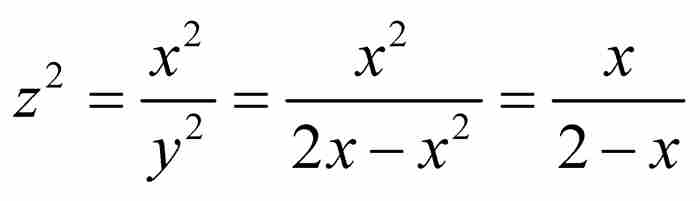 ,从中解出
,从中解出
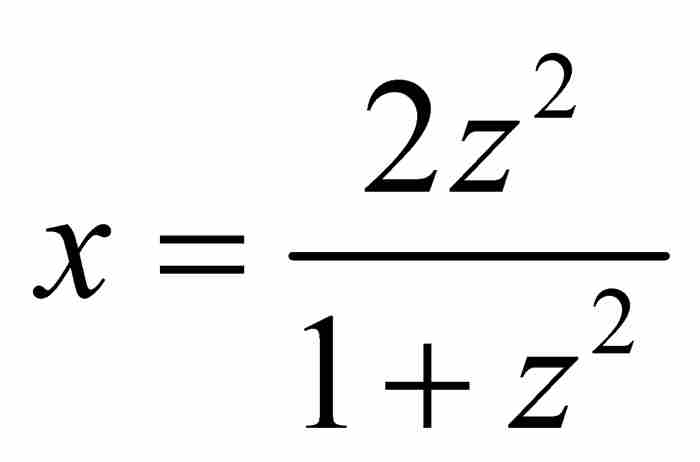 (7)
(7)
挑战在于计算图2-9中阴影区域的面积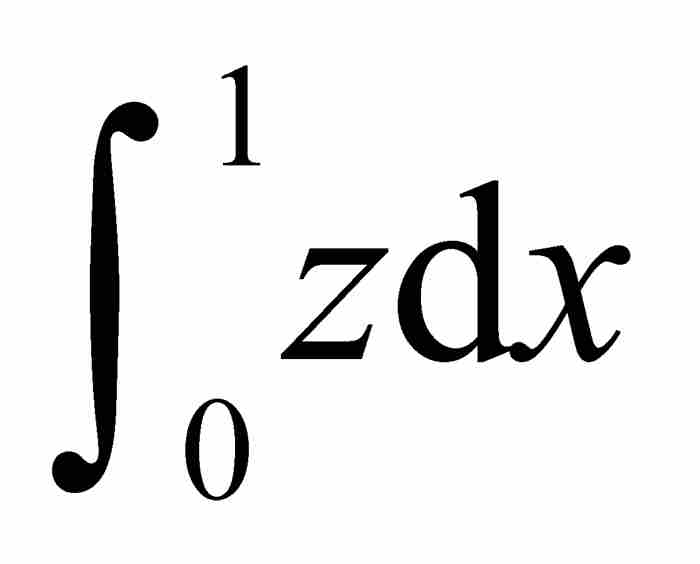 。考虑割圆曲线
。考虑割圆曲线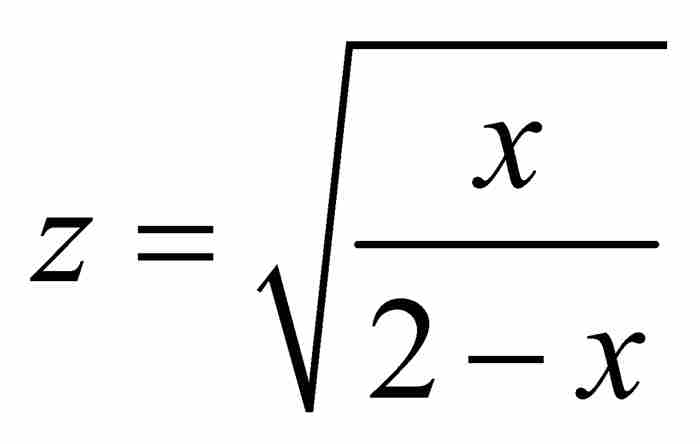 的图形,并按上述推导过程,证实
的图形,并按上述推导过程,证实
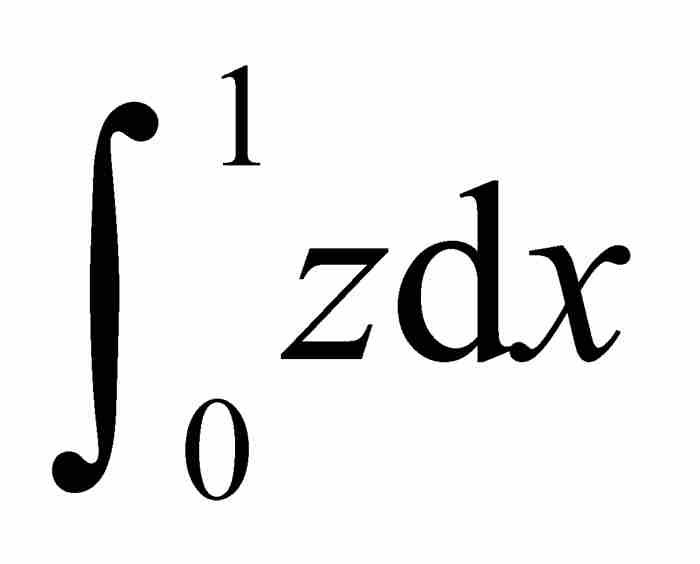 =面积(阴影区域)
=面积(阴影区域)
=面积(正方形)-面积(上方区域)=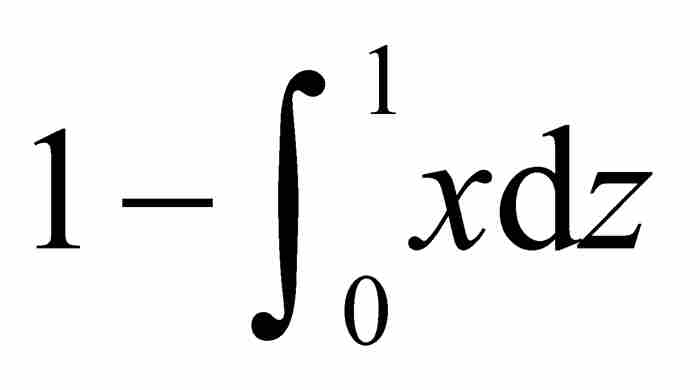 (8)
(8)
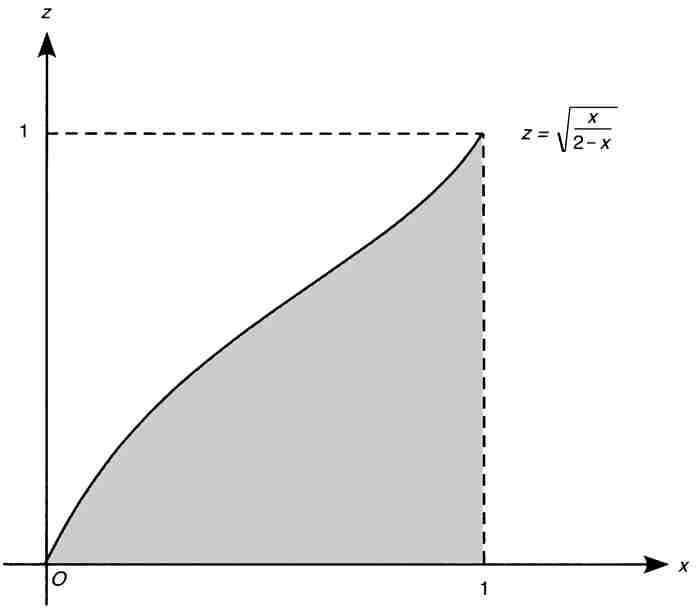
图 2-9
回到变换定理,莱布尼茨把式(7)和式(8)结合起来,得到
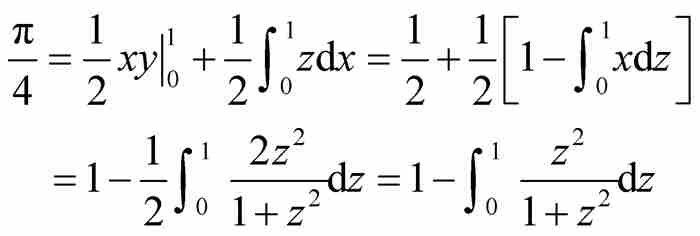
他将最后的被积函数重写成
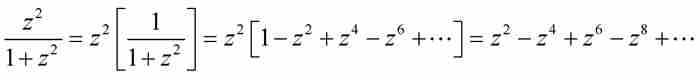
其中方括号内出现了一个等比级数。据此,莱布尼茨推断
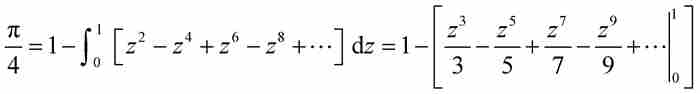
化简成
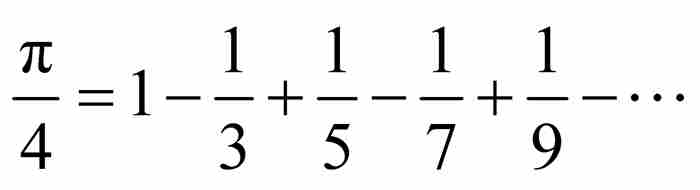 (9)
(9)
这就是莱布尼茨级数。
这是一个奇妙的级数。它的项遵循一个极为普通的模式:带有交替正负号的奇数的倒数。然而最重要的是,这个看似不起眼的表达式的和为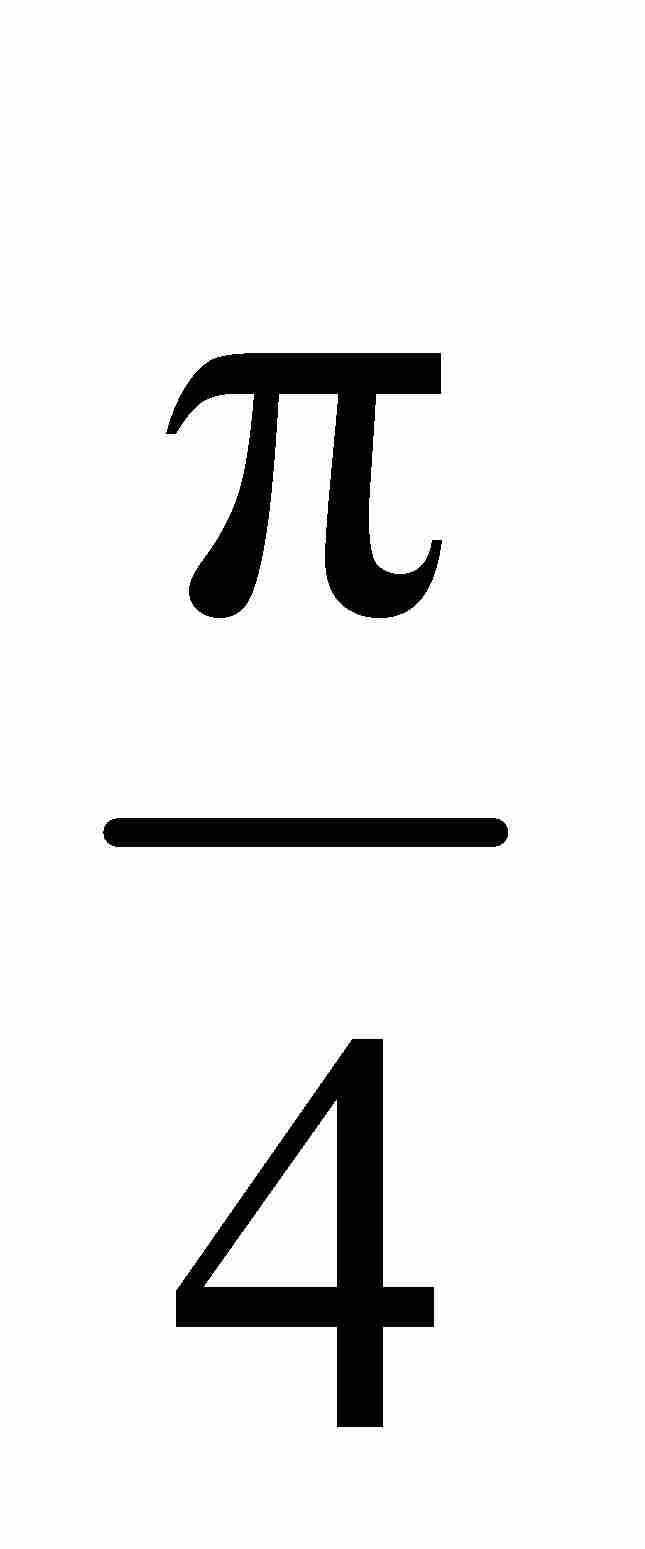 。莱布尼茨回忆当他第一次将这个结果同惠更斯交流时,他得到热烈的赞扬,因为“惠更斯给予了极高的评价,并且在退回这篇论文的附信中说,这在数学家中是一个值得永远记住的发现”。1
。莱布尼茨回忆当他第一次将这个结果同惠更斯交流时,他得到热烈的赞扬,因为“惠更斯给予了极高的评价,并且在退回这篇论文的附信中说,这在数学家中是一个值得永远记住的发现”。1
1 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 46。
按照莱布尼茨的说法,这个发现的意义在于“第一次证明了圆的面积恰好等于有理数的一个级数”。2 也许有人会对他用“恰好”一词挑毛病,但是很难同他的热情争辩。
2 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 47。
他追加了一个离奇的补遗。通过对式(9)两端除2,并组合其中的项,莱布尼茨发现
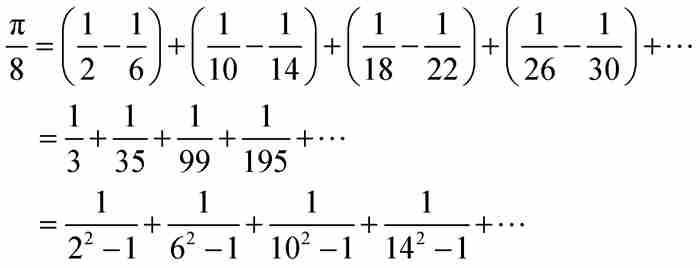
就是说,这个等式表明,如果我们从2开始对每个相间的偶数的平方减1的倒数求和,结果为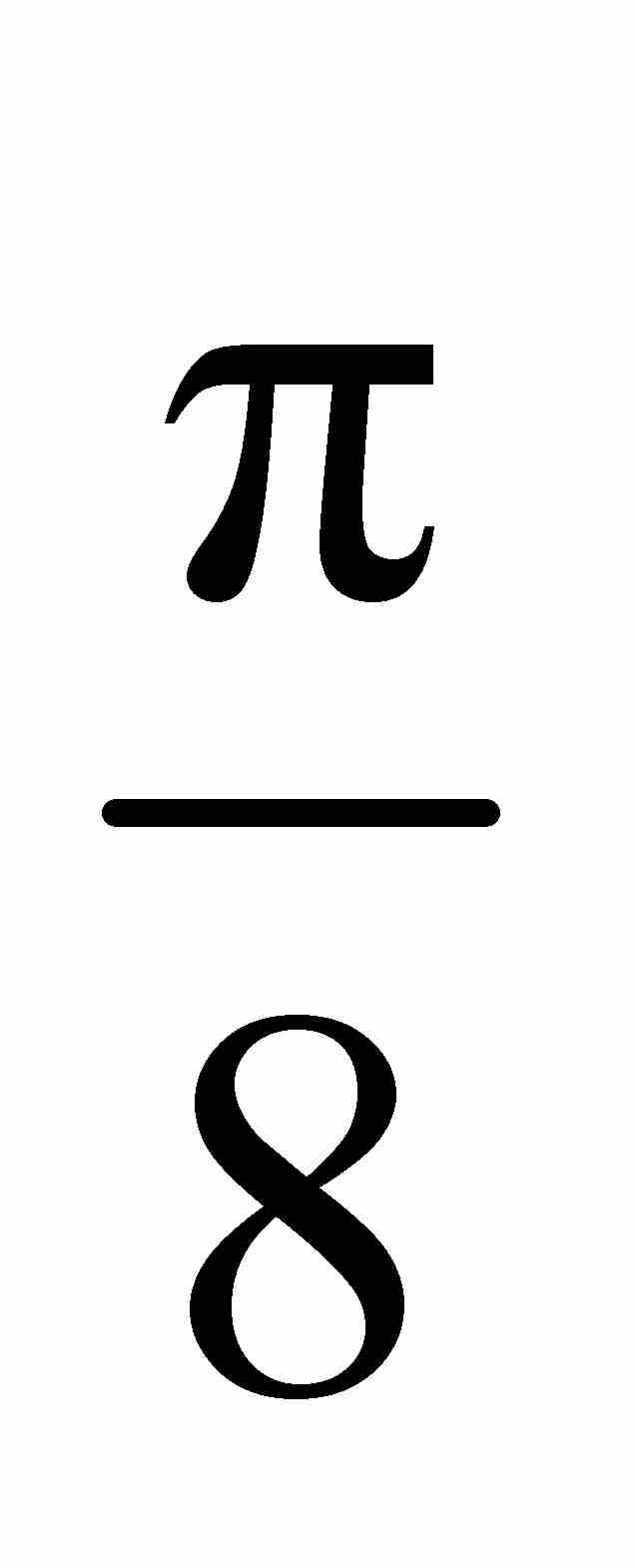 。多么神奇!这提醒人们,分析学家手中的公式近乎魔术一般。
。多么神奇!这提醒人们,分析学家手中的公式近乎魔术一般。
莱布尼茨级数在形式上是著名的,但如果用它计算π的近似值则毫无价值。这个级数是收敛的,不过收敛极为缓慢。如果对莱布尼茨级数的前300项求和,仅能得到π的精确到一位小数的近似值。这么糟糕的精度是不值得费力地去求和的。但是,我们将会看到,在欧拉手中,一个相关的无穷级数将产生一个高效的计算π的近似值的方法。
毫无疑问,莱布尼茨级数是一个微积分学的杰作。然而,按照惯例,当讨论这些早期的结果时,我们必须提出一些注意事项。值得一提的第一件事,是变换定理使用了无穷小推理。另一件事,是莱布尼茨在求其级数的值时需要用无限多积分项之和代替无限多项之和的积分,这样一个步骤,它的微妙性将成为未来几个世纪面对的问题。
同时,还有另外一个问题:莱布尼茨并不是第一个发现这个级数的人。英国数学家詹姆斯·格雷戈里在其几年前已经发现一个非常相似的级数。事实上,格雷戈里得到了反正切函数的展开式,即
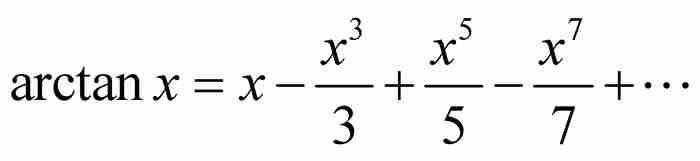
当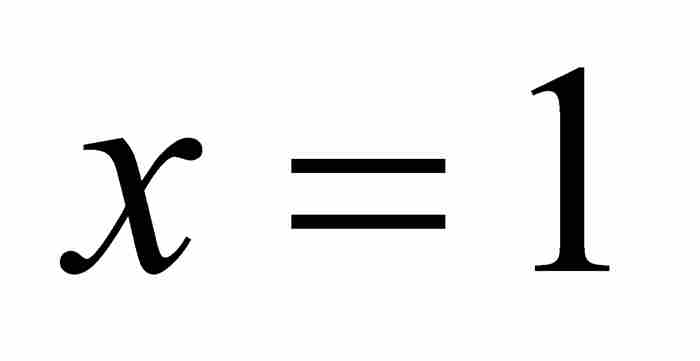 时,这就是莱布尼茨级数(虽然格雷戈里也许实际上并未作过代换,没有将这个函数级数转换成数值级数)。
时,这就是莱布尼茨级数(虽然格雷戈里也许实际上并未作过代换,没有将这个函数级数转换成数值级数)。
在1674年,作为数学新手的莱布尼茨并不知道格雷戈里的成果,并相信他自己找到了新东西。这反过来让他的英国对手对他投以怀疑的目光。对他们来说,莱布尼茨具有攫取他人成果的倾向。这些怀疑在18世纪初期自然会被进一步放大,因为那时在牛顿亲自指挥下,整个英国都在指责莱布尼茨剽窃微积分的抄袭行为。级数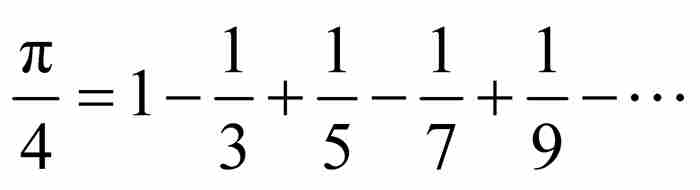 中的这笔糊涂账被当作是莱布尼茨背信弃义的最初例证。
中的这笔糊涂账被当作是莱布尼茨背信弃义的最初例证。
但是,即使是格雷戈里也不是第一个涉足这条道路的人。我们在前一章中提到的印度数学家尼拉坎塔在一本名为Tantrasangraha的书中描述了这个级数,还是用韵文的形式。3 虽然这一成果在莱布尼茨时代的欧洲尚不为人知,但这件事提醒世人,数学是全人类的事业。
3 Ranjan Roy, “The Discovery for the Series Formula for π by Leibniz, Gregory and Nilakanta, ” Mathematics Magazine, vol. 63(1990),no. 5, pp. 291-306。
尽管有格雷戈里和尼拉坎塔的成果,但是我们知道莱布尼茨的级数推导不是剽窃行为。后来他在1674年写道,不论是他还是惠更斯“或者任何一个在巴黎的其他人,完全没有听说过任何关于通过有理数的无穷级数表示圆面积的报道”。4 像发明通常的微积分一样,莱布尼茨级数是一项属于个人的成就。
4 J. M. Child (trans.), The Early Mathematical Manuscripts of Leibniz, Open Court Publishing Co., 1920, p. 46。
在接下来的20多年里,当莱布尼茨完善、整理并且发表了他关于微分学和积分学的思想后,这个新手变成为一位大师。在这样的起点上,这门学科将在未来的一个世纪发展起来——事实上将迅猛地成长s。我们将继续讲述这个故事,谈谈他在瑞士的两位最著名的追随者,即伯努利兄弟二人。