典型案例

你不知道你已经死了。因为，如果你没死，那么你不知道你已经死了；如果你已经死了，那么你也不知道你已经死了。你或者没死，或者已经死了，总之你不知道你已经死了。

逻辑辨析

在上述证明中，有三个重要的前提，其中两个是事实判断或者说经验判断：“如果你没死，那么你不知道你已经死了”和“如果你已经死了，那么你也不知道你已经死了”。还有一个关键的前提是：“你或者没死，或者已经死了”。该判断指出，对于一个人只能有两种情况：你或者没死，或者已经死了。如果存在第三种情况，那么上述证明就存在漏洞，需要继续证明在第三种情况下，你仍然不知道你已经死了。

一个严谨的证明需要穷尽所有可能的情况。在日常思维中，不光证明如此，在定义概念、做出判断、进行论证的过程中，都必须考虑所有可能的情况。

知识链接

所谓思维的严密性，指的是在同一思维过程中，我们必须考虑思维所涉及的所有可能的情况，并且对各种可能情况都要做出明确的断定，或者肯定之，或者否定之。

思维严密性的要求主要包括两个方面：

一、概念要清晰

就概念而言，思维的严密性要求在同一时间、同一地点对同一对象是否具有某一属性要有清晰的断定，在同一个概念中，不能既不断定对象具有某一属性，又不断定对象不具有某一属性。一个概念如果违反了这一要求，则称之为“模糊概念”，如“无可无不可”就是一个模糊概念。

二、判断要明确

就判断而言，思维的严密性要求在同一思维过程中，对于事物的可能情况，必须做出明确的断定，不能既否定某对象是什么，又否定它不是什么。

严格地说，思维的严密性要求可以用下列形式来表示：

A_{1或者A2或者……或者An-1或者An}

其中，A_{1，A2，…，An-1，An已经穷尽了所有可能的情况，不存在除了A1，A2，…，An-1，An之外的情况。}

扩展延伸

在实际的思维过程中，经常会发生违反思维严密性的情况，例如：

（1）究竟是先有鸡还是先有蛋？

（2）你是为党说话还是为人民说话？

上述两个例子都违反了思维的严密性原则。在例（1）中，提问基于一个假设：要么先有鸡，要么先有蛋。这是一个错误的假设，因为对于鸡和蛋的先后比较而言，可能有三种情况：先有鸡；先有蛋；鸡和蛋没有先后之分（也许有人会指出另一种情况：既是先有鸡又是先有蛋，但这是不可能的，因此只能有上述三种情况）。例（1）中的提问忽略了第三种情况，违反了思维的严密性。实际上，对于鸡和蛋的先后比较而言，确实是没有先后之分的，它本身是一个逐渐进化的过程，谈不上孰先孰后。类似的问题还如：对于整数而言，先有奇数还是先有偶数？在例（2）中，提问者给予一个假设：要么为党说话，要么为人民说话。这也是一个错误的假设，因为对于为谁说话而言，可能有四种情况：为党说话而不为人民说话；为人民说话而不为党说话；既为党说话又为人民说话；既不为党说话又不为人民说话。例（2）中的提问忽略了后面两种情况，严重违反了思维的严密性。又如：

（1）在如何对待传统文化的讨论中，有两种观点分别认为：传统文化有些应该继承，有些不应该继承。李娟认为这两种观点都是正确的，而王娟认为这两种观点都是错误的。

（2）某镇长在向上级领导汇报工作时信誓旦旦地表示：“我们镇的每一项工作都非常出色”，但是当他面对媒体的质疑时又转而表示：“我们镇的某些工作不是非常出色”。此事被网络曝光，该镇长又出来解释说：我既不赞成“我们镇的每一项工作都非常出色”，也不赞成“我们镇的某些工作不是非常出色”。

在上例（1）中，“传统文化有些应该继承”和“传统文化有些不应该继承”是不能都加以否定的，其中必须至少肯定一个。李娟认为这两种观点都是正确的，这并不违反思维的原则；王娟认为这两种观点都是错误的，违反了思维的严密性。在上例（2）中，“我们镇的每一项工作都非常出色”和“我们镇的某些工作不是非常出色”是既不能同时肯定，又不能同时否定的，必须肯定其一，否定其一。该镇长开始都加以肯定，犯了“自相矛盾”的错误，后来又都加以否定，两头放水，违反思维的严密性。

在日常生活中，有时由于特殊原因，一时拿不准情况或者不想明确表态，这不能说是违反思维的严密性。例如：

（1）唐朝初期著名诗人苏味道仕途顺利，官运亨通，仅做宰相就长达数年之久，但他在位时并没做出什么突出成绩来。他老于世故，处事圆滑。他曾经对人说：“处事不欲决断明白，若有错误，必贻咎谴，但模棱以持两端可矣。”时人由是号为“苏模棱”。（《旧唐书·苏味道传》）

（2）傅二棒锤又扭捏了半天，说道：“不瞒老师说：老师大远的带了门生到这外洋来，原想三年期满，提拔门生得个保举，以便将来出去做官便宜些；谁料平空里出了这个岔子，现在保举是没有指望。这是门生自己没有运气，辜负老师栽培，亦是没法的事。门生现在求老师赏个札子，不为别的，为的是将来回国之后，说起来面子好看些。虽说门生没有一处处走到，到底老师委过门生这们一个差使，将来履历上亦写着好看些。”

温钦差听了一笑，也不置可否。你道为何？原来温钦差的为人极为诚笃，说是委了差使不去，这事便不实在，所以他不甚为然，因之没有下文。（《官场现形记》第五十六回）

“模棱两可”实际意味“模棱两不可”，凡事不做决断、不置可否。准确地说，在上例（1）中，苏味道对于两个互相矛盾的判断都不做决断、不置可否，并不违反思维的严密性。上例（2）中，温钦差的不置可否，也不违反思维的严密性原则。

勤思多练

1.试从思维严密性的角度分析下列论证。

（1）试分析前文提到的“半费之讼”：

古希腊有一个名叫欧提勒士的人，他向著名的辩者普罗泰戈拉学习法律。两人曾签订协议，约定在欧提勒士毕业时付一半学费给普罗泰戈拉，另一半学费则等欧提勒士毕业后第一次打赢官司时付清。

但毕业后，欧提勒士一直没有打官司。普罗泰戈拉等得不耐烦了，于是向法庭提起诉讼，状告欧提勒士，他做了如下推理：如果欧提勒士在这场官司中胜诉，那么按协议的约定，他应付给我另一半学费；如果欧提勒士在这场官司中败诉，那么按法庭的判决，他也应付给我另一半学费；他这场官司或者胜诉或者败诉，总之他都应付给我另一半学费。

而欧提勒士则认为：如果我这场官司胜诉，那么按法庭的判决，我不应付给普罗泰戈拉另一半学费；如果我这场官司败诉，那么，按协议的约定，我也不应付给普罗泰戈拉另一半学费；我这场官司或者胜诉或者败诉，总之我不应付给他另一半学费。

（2）《高中数学·选修2—2》（人教版）中有这样一道题：

用数学归纳法证明1^{2+22+32+…+n2=（n（n+1）（2n+1））/6。}

证明：

①当n=1时，左边=1^{2=1，右边=（1×2×3）/6=1，等式成立。}

②假设当n=k时，等式成立，即

1^{2+22+32+…+k2=（k（k+1）（2k+1））/6}

则有

这就是说，当n=k+1时等式也成立。

根据①和②，可知等式对任何n∈Ν*都成立。

2.（综合练习）试从思维的同一性、一致性以及严密性的角度分析下列论述。

（1）上帝是否能够制造出一块连他自己也举不起来的石头？如果上帝能制造出一块连他自己也举不起来的石头，那么他不是万能的，因为有一块石头他举不起来；如果上帝不能制造出一块连他自己也举不起来的石头，那么他也不是万能的，因为有一块石头他造不出来。上帝或者能制造一块连他自己也举不起来的石头，或者不能制造一块连他自己也举不起来的石头，总之，他都不是万能的。

（2）鲁迅《论辩的魂灵》中写道：

“洋奴会说洋话。你主张读洋书，就是洋奴，人格破产了！受人格破产的洋奴崇拜的洋书，其价值从可知矣！但我读洋文是学校的课程，是政府的功令，反对者，即反对政府也。无父无君之无政府党，人人得而诛之。”

“你说中国不好。你是外国人么？为什么不到外国去？可惜外国人看你不起……。”

“你说甲生疮。甲是中国人，你就是说中国人生疮了。既然中国人生疮，你是中国人，就是你也生疮了。你既然也生疮，你就和甲一样。而你只说甲生疮，则竟无自知之明，你的话还有什么价值？倘你没有生疮，是说诳也。卖国贼是说诳的，所以你是卖国贼。我骂卖国贼，所以我是爱国者。爱国者的话是最有价值的，所以我的话是不错的，我的话既然不错，你就是卖国贼无疑了！”

“自由结婚未免太过激了。其实，我也并非老顽固，中国提倡女学的还是我第一个。但他们却太趋极端了，太趋极端，即有亡国之祸，所以气得我偏要说‘男女授受不亲’。况且，凡事不可过激；过激派都主张共妻主义的。乙赞成自由结婚，不就是主张共妻主义么？他既然主张共妻主义，就应该先将他的妻拿出来给我们‘共’。”

“丙讲革命是为的要图利：不为图利，为什么要讲革命？我亲眼看见他三千七百九十一箱半的现金抬进门。你说不然，反对我么？那么，你就是他的同党。呜呼，党同伐异之风，于今为烈，提倡欧化者不得辞其咎矣！”

“丁牺牲了性命，乃是闹得一塌糊涂，活不下去了的缘故。现在妄称志士，诸君切勿为其所愚。况且，中国不是更坏了么？”

“戊能算什么英雄呢？听说，一声爆竹，他也会吃惊。还怕爆竹，能听枪炮声么？怕听枪炮声，打起仗来不要逃跑么？打起仗来就逃跑的反称英雄，所以中国糟透了。”

“你自以为是‘人’，我却以为非也。我是畜类，现在我就叫你爹爹。你既然是畜类的爹爹，当然也就是畜类了。”

（3）你认识那个藏起来的人？不认识。而他是你父亲，所以，你不认识你的父亲。

（4）马者，所以命形也。白者，所以命色也。命色者，非命形也，故曰白马非马。（《公孙龙子·白马论》）

（5）“日方中方睨，物方生方死。”（《庄子·天下》）“方生方死，方死方生。方可方不可，方不可方可。”（《庄子·齐物论》）

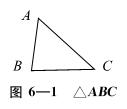
（6）已知：△ABC中，∠B＞∠C，如图6—1：

求证：AC＞AB。

证明：如果AC不大于AB，那么或者AC＝AB，或者AC＜AB。

如果AC＝AB，则∠B＝∠C；如果AC＜AB，则根据三角形中大边对大角的性质，将有∠B＜∠C。这两种情况均与已知条件∠B＞∠C相矛盾。所以假设不成立。由此可见，AC＞AB。

（7）中国历史上有一个著名的哲学家叫王阳明。有一次他带了两个学生到一个朋友家里去做客。

他的朋友养了两只鹅，一只会叫一只不会叫。朋友吩咐仆人把那只不会叫的鹅杀掉招待王阳明。王阳明用这件事教育他的两个学生说：“你们看，不会叫的鹅被宰了，而会叫的还活着。你们要记住这个哲理：有才的才能长寿。”

吃过饭后，他们到屋后山上去散步，见山上有两棵大树，一棵长得很直，是个栋梁之材；另一棵则弯弯曲曲，不能成材。两个匠人正在锯那一棵长得很直的树。王阳明又用这件事教育他的学生说：“你们看，挺立的树可以作为栋梁，结果被锯了；而弯曲的树不能成材，却被留下来了。你们要记住这个哲理：无才的才能长寿。”

两个学生有点糊涂了，到底是“有才的才能长寿”还是“无才的才能长寿”？其中一个学生忍不住问王阳明说：“先生，您不是说过‘有才的才能长寿’吗？”王阳明回答说：“是的，我是这样说过。”另一个学生又问：“先生，您刚才不是说‘无才的才能长寿’吗？”王阳明回答说：“是的，我是这样说的。”两个学生面面相觑，感到茫然不解。

（8）一个人有满头秀发，当然不能说她是秃头。她掉了一根头发，仍然不是秃头。按照这个道理，让一个不是秃头的人一根一根地减少头发，最后可得出一条结论：没有一根头发的光头也不是秃头！

（9）世称纣力能索铁伸钩，又称武王伐之兵不血刃。夫以索铁伸钩之力当人，则是孟贲、夏育之匹也；以不血刃之德取人，则是三皇、五帝之属也。以索铁之力，不宜受服，以不血刃之德，不宜顿兵。今称纣力，则武王德贬；誉武王，则纣力少。索铁、不血刃，不得两立；殷、周之称，不得二全。不得二全，则必一非。（《论衡·语增》）